Rajasthan Board RBSE Class 12 Maths Chapter 15 Linear Programming Ex 15.2
Question 1.
A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs ₹5/kg to purchase food ‘I’ and ₹7/kg to purchase food ‘II’. Formulate this problem as a LPP to minimize the cost of such a mixture and solve it graphically.
Solution:
Let x kg of food I andy kg of food II in mixture. According to question,
Cost of x kg food @ ₹5 per kg = ₹5x
and cost of y kg food @ ₹ 7 per kg = ₹ 7y
∴ Total cost of mixture = ₹(5x + ly)
Total units of vitmain A in x kg of food I in mixutre = 2x
and total units of vitamin A in y kg of food II in mixture = y
∴ according to question,
2x + y ≥ 8 …..(1)
Total units of vitamin C in x kg of food I in mixture = x and total units of vitamin C iny kg of food II in mixture = 2y
∴ According to question,
x + 2y ≥ 10 …..(2)
and x ≥ 0, y ≥ 0
∴ Mathematically formulation of LPP is
Minimum value of cost function Z = 5x + 7y
Subject to the constraints
2x + y ≥ 8
x + 2y ≥ 10
x ≥ 0, y ≥ 0
Converting the inequation into the equation
2x + y = 8
x + 2y = 10
Region represented by 2x + y ≥ 8 : The line 2x + y = 8 meets the coordinate axis at A(4, 0) and B(0, 8).
2x + y = 8
Join the points A to B to obtain the line. Clearly (0, 0) does not satisfy the given inequation 2(0) + 0 = 0 ≥ 8. So the region opposite to the origin represents the solution set of the inequation.
Region represented by x + 2y ≥ 10 : The line x + 2y = 10 meets the coordinate axis at the points C(10, 0) and D(0, 5).
x + 2y = 10
| X | 10 | 0 |
| y | 0 | 5 |
C(10,0);D(0,5)
Join the points C and D to obtain the line. Clearly (0, 0) does not satisfy the given inequation 0 + 2(0) = 0 ≥ 10.
So the region opposite to the origin represents the solution set of the inequation.
Region represented by x ≥ 0,y ≥ 0 : Since every point in first quadrant satisfies these equations. So the first quadrant is the region, represented by the inequation x ≥ 0 and y ≥ 0.
The coordinate of the point of intersection of lines 2x + y = 8 and x + 2y = 10 are x = 2 and y = 4.
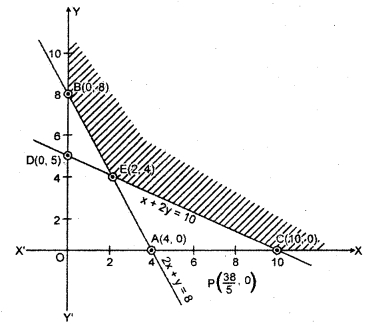
Shaded region CEB represents the common region of the inequations. This region is the feasible solution region of the inequations. The coordinates of the comer points are C(10, 0), E(2,4) and B(0,8).
The value of the objective function on these points are given in the following table :
| Point | x-coordinate | y-coordinate | Objective function Z = 5x + 7y |
| C | 10 | 0 | Zc= 5 x 10+7 x 0 = 5 |
| E | 2 | 4 | ZE = 5 x 2+7 x 4 = 38 |
| B | 0 | 8 | ZB = 5 x 0 + 7 x 8 = 56 |
In the above table value of objective function Z is minimum and Z = ₹38 at x = 2 and y = 4.
Because feasible region is open. Therefore open region of inequation 5x + 7y ≤ 38 does not have any common feasible point.
So the mixture has 2 kg of food I and 4 kg of food II in mixture and its minimum cost = ₹38.
Question 2.
A housewife wishes to mix together two kinds of food, X and F in such a way that the mixtures contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C.
The vitamin contents of one kg of food are given below :
| Vitamin A | Vitamin B | Vitamin C | |
| Food X | 1 | 2 | 3 |
| Food Y | 2 | 2 | 1 |
One kg of food X costs ₹6 and one kg of food F cost ₹10. Find the least cost of the mixture which will produce the diet.
Solution :
Let x kg of food X and Y kg of food F are mixed together to make the mixture.
Since one kg of food X contains one unit of Vitamin A and one kg of food Y contains 2 units of Vitamin A.
Therefore x kg of food X and y kg of food Y will contain x + 2y units of Vitamin A. But the mixture should contain at least 10 units of Vitamins A. Therefore,
x + 2y ≥ 10
Similarly, x kg of food Xand y kg of food F will produce 2x + 2y units of Vitamin B and 3x + y units of Vitamin C. But minimum requirements of Vitamin B and Vitamin C are respectively of 12 and 8 units.
Therefore,
2x + 2y ≥ 12 and 3x + y ≥ 8
Since, the quantity of food X and food y cannot be negative.
∴ x ≥ 0, y ≥ 0
It is given that one kg of food X costs ₹6 and one kg of food Y costs ₹10. So, x kg of food X and y kg of food Fwill cost ₹(6x + 10y).
Thus, the given linear programming problem is
Minimize Z = 6x +10y
Subject to the constraints,
x + 2y ≥ 10
2x + 2y ≥ 12
3x + y ≥ 8
and x ≥ 0, y ≥ 0
Converting the inequation into equations
x + 2y – 10
2x + 2y = 12
3x + y = 8
Region represented by x + 2y ≥ 10 : The line x + 2y = 10, meets the coordinate axis at ,A(10, 0) and B(0, 5).
x + 2y = 10
| X | 10 | 0 |
| y | 0 | 5 |
A (10, 0); 5(0,5)
Join the points A and B to obtain the line. We find that, the point (0, 0) does not satisfy the inequation x + 2y ≥ 10. So, the region opposite to the origin represents the solution set of the inquation.
Region represented by 2x + 2y ≥ 12 : The line 2x + 2y = 12, meets the coordinate axis at C(6, 0) and D(0, 6).
2x + 2y = 12
| X | 6 | 0 |
| y | 0 | 6 |
C(6, 0); D(0, 6)
Joint the points C and D to obtain the line. We find that, the point (0, 0) does not satisfy the inequation 2x + 2y ≥ 10. So, the region opposite to the origin, represents the solution set of the inequation.
Region represented by 3x + y ≥ 8 : The line 3x + y = 8 meets the coordinate axis at E (\(\frac { 8 }{ 3 } \),0);F(0,8)
3x + y = 8
| X | \(\frac { 8 }{ 3 } \) | 0 |
| y | 0 | 8 |
E (\(\frac { 8 }{ 3 } \),0); F(0,8)
Join the points E and F to obtain the line. We find that, the point (0,0) does not satisfy the inequation 3x + y ≥ 8. So, the region opposite to the origin repesents the solution set of the inequation.
Region represented by x ≥ 0, y ≥ 0: Since every point in the first quadrant satisfies the inequations. So, the first quadrant is the region represented by the inequation x ≥ 0 and y ≥ 0.
The shaded region AGHB represents the region of the above inequations. This region the feasible region of the given LLP.
The coordinates of the comer points of the shaded feasible region are .4(10, 0), G(2, 4), H(1, 5) and B(0, 8).
Where the points G and H have been obtained by solving the equations of the corresponding intersecting lines, simu-ltaneously.
The value of the objective function at these points are given in the following table :
| Point | x-coordinates | y-coordinates | Objective function Z = 6x + 10y |
| A | 10 | 0 | ZA = 6(10) + 10(0) = 60 |
| G | 2 | 4 | ZG = 6(2) + 10(4) = 52 |
| H | 1 | 5 | ZE = 6(1) + 10(5) = 56 |
| B | 0 | 8 | ZB = 6(0)+ 10(8) = 80 |
Clearly, Z is minimum at x = 2 and y = 4. The minimum value of Z is 52.
We observe that the open half plane represented by 6x + 10y < 52 does not have points in common with the feasible region. So, Z has minimum value equal to 52.
Hence, the least cost of the mixture is ₹52.
Question 3.
One kind of cake requires 300 kg of flour and 15 g of fat and another kind of cake requires 150 g of flour and 30 g of fat, find the maximum number of cakes which can be made from 7.5 kg of flour and 600 g of fat assuming that there is no shortage of the other ingredients used in making the cakes. Formulate the LPP solve the problem by graphical method.
Solution:
Let x cakes are made of one kind and y cakes are made of another kind. Therefore objective function of maximum limit = x + y.
⇒ Z = x + y
Firstly according to question, there is 300x gm flour in one kind and 150y gm in another kind.
∴ 300x + 150y ≤ 7500 gm
Secondly according to question, there is 15x gm fats in one kind of cake and 30y gm fats is in another kind.
∴ 15x + 30y ≤ 600 gm
∵ The number of cakes can never be negative so x ≥ 0 and y ≥ 0.
Therefore mathematically formulation of Linear Programming Problem is the following :
Maximum Z = x + y
Subject to the constraints
300x + 150y ≤ 7500
15x + 30y ≤ 600
x ≥ 0, y ≥ 0
Converting the given inequations into equations
300x + 150y ≤ 7500
⇒ 2x + y = 50 …..(1)
and 15x + 30y = 600
⇒ x + 2y = 40 …..(2)
Region represented by 2x + y ≤ 50 : The line 2x + y = 50, meets the coordinate axis at A(25, 0) and B(0, 50).
2x + y = 50
| X | 25 | 0 |
| y | 0 | 50 |
A(25, 0); B(0, 50)
Join the points A and B to obtain the line. Clearly, (0,0) satisfies the inequation 2 × 0 + 0 ≤ 50. So, the region containing the origin represents the solution set of the inequation.
Region represented by x + 2y ≤ 40 : The line x + 2y = 40 meets the coordinate axis at C(40,0) and D(0, 20).
x + 2y = 40
| X | 40 | 0 |
| y | 0 | 20 |
C(40, 0); D(0, 20)
Join the points C and D to obtain the line. Clearly (0, 0) satisfies the inequation (0 + 2 × 0) < 40. So, the region containing the origin represents the solution set of the inequation.
Region represented by x ≥ 0, y > ≥ : Since every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The shaded region OAED represents the common region of the above inequations. This region is the feasible region of the given LPP.
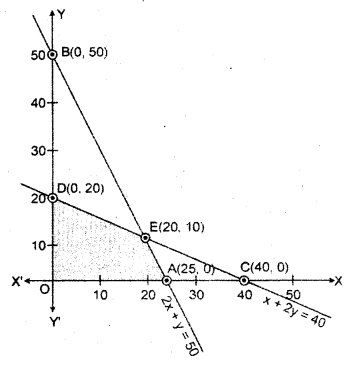
The coordinates of the comer-points of the shaded feasible region are O(0,0), C(25,0), E(20,10) and B(0, 20).
The point E has been obtained by solving the equations of the corresponding intersecting lines, simultaneously.
The value of the objective function of these points are given in the following table :
| Point | x-coordinate | y-coordinate | Objective function Z = x + y |
| O | 0 | 0 | Z = x + y |
| A | 25 | 0 | ZA = 25 + 0 = 25 |
| E | 20 | 10 | ZE = 20 + 10 = 30 |
| D | 0 | 20 | ZD= 0 + 20 = 20 |
It is clear from the table that objective function has maximum value at point E(20, 10).
Hence there are 20 cakes of one kind and 10 cakes of another kind. Maximum number of cakes = 20 + 10 = 30.
Question 4.
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hour on machine B to produce a package of nuts, it takes 3 hour of work on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 2.50 per pacakge on nuts and ₹ 1 per package on bolts. How many pacakges of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day ? Translate this problem mathematically and then solve it
Solution:
Let he should make x packets of nuts and y packets of bolts to get maximum profit.
He gets profit of ₹ 2-50 per package of nuts and ₹1 per package of bolts.
∴ Objective function, Z = 2.50 x + y
He works maximum of 1 hours on machine A and 3 hours on machine B.
∴ \(\frac { x }{ 1 } \) + \(\frac { y }{ 3 } \) ≤ 12
⇒ 3x + y ≤ 36 …..(1)
and he works maximum of 3x hour on machine A and 1 hour on machine B.
∴ \(\frac { x }{ 3 } \) + \(\frac { y }{ 3 } \) ≤ 12
⇒ x + 3y ≤ 36 ……(2)
Because x and y are the number of nut and bolt so it can not be negative.
∴ x ≥ 0 and y ≥ 0
Mathematically formulation of Linear Programming Problem is as following :
Maximum Z = 2.50x + y
Subject to the constraints
x + 3y ≤ 36
3x + y ≤ 36
x ≥ 0, y ≥ 0
Converting the inequations into equations
x + 3y = 36
3x + y = 36
Region represented by x + 3y ≤ 36 : Line x + 3y =12
meets the coordinate axis at the points A( 12,0) and B(0, 4).
x + 3y = 36
| X | 36 | 0 |
| y | 0 | 12 |
A(36,0);B(0, 12)
Join the points A to 5 to obtain the line. Clearly (0, 0) satisfies the given inequation
0 + 3(0) = 0 ≤ 36.
So the origin containing the region represents the solution set of the inequation x + 3y ≤ 36.
Region represented by 3x + y ≤ 36 : The line 3x + y = 36, meets the coordinate axis at C(12,0) and D(0, 12).
3x + y = 36
| X | 12 | 0 |
| y | 0 | 36 |
C(12, 0); D(0, 36)
Join the points C and D to obtain the line.
Clearly, (0, 0) satisfies the inequation 3x + y ≤ 36. So, the region containing the origin represents the solution set of the inequation 3x + y ≤ 36.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
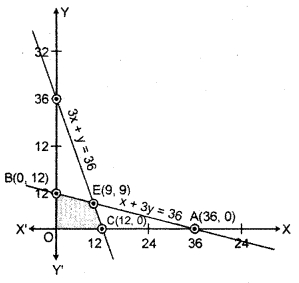
E (9, 9) is the point of intersection of lines 3x + y = 36 and x + 3y = 36 shaded region OCEB represents the common region of the inequations. This region is the feasible solution set the given L.P.P.
The comer points of this feasible solution region are O(0, 0), C(12,0), E{9, 9) and B(0, 12).
The value of objective function on these points is as following :
| Point | x-coordinate | y-coordinate | Objective function Z = 2.50 x + y |
| O | 0 | 0 | ZO = 2.50(0) + 0 = 0 |
| C | 12 | 0 | Zc = 2.50(12) + 0 = 30 |
| E | 9 | 9 | ZE = 2.50(9) + 9 = 31.50 |
| B | 0 | 12 | ZB= 2.50(0) + 12 = 12 |
It is clear from the table that objective function Z = 2.50x + y has maximum value at point E(9,9). Hence manufacture should make nine packets of each nut and bolts daily to get maximum profit ₹ 31.50.
Question 5.
A dealer wishes to purchase a number of fans and sewing machines. He has only ₹5760 to invest and has space for at most 20 items. A fan costs him ₹360 and a sewing machine ₹240. His expectation is that he can sell a fan at a profit of ₹22 and a sewing machine at a profit of ₹18. Assuming that he can sell all the items that he can buy. How should he invest his money in order to maximize his profit ? Formulate this problem mathematically and then solve it.
Solution:
Let dealer should purchase x fans andy sewing machines.
∴ the cost of x fans = ₹ 360x
and the cost of y sewing machines = ₹ 240y
∴ According to question,
360x + 240 ≤ 5760
According to place available to have x fans andy sewing machines x + y ≤ 20.
The profit earned by dealer on x fans = ₹22x
and profit earned on y sewing machines = ₹18y
∴ To earn maximum profits objective function
Z = 22 x + 18y
Mathematically formulation of LPP is as following :
Maximum Z = 22x + 18y
Subject to the constraints
360x + 240y ≤ 5760
x + y ≤ 20
x ≥ 0, y ≥ 0
Converting the given inequations into equations
360x + 240y = 5760
⇒ 3x + 2y = 48 …..(1)
and x + y = 20 ……(2)
Region represented by 3x + 2y ≤ 48 : The line 3x + 2y = 48, meets the coordinate axis at A(16, 0) and B(0, 24).
3x + 2y = 48
| X | 16 | 0 |
| y | 0 | 24 |
A(16,0);B(0,24)
Join the points A and B to obtain the line. Clearly (0, 0) stisfies the inequation 3 × 0 + 2 × o = 0 ≤ 48. So, the region containing the origin represents the solution set of the inequation.
Region represented by x + y ≤, 20 : The line x + y = 20 meets at the point E(20, 0) and F(0, 20).
x + y = 20
| X | 20 | 0 |
| y | 0 | 20 |
C(20, 0); D(0, 20)
Join the points E and F to obtain the line. Clearly (0,0), satisfies the inequation 0 + 0 ≤ 20. So, the region containing the origin represents the solution set of the inequation.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequation. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The shaded region OAED represents the common region of the above inequations. This region is the feasible region of the given LPP.
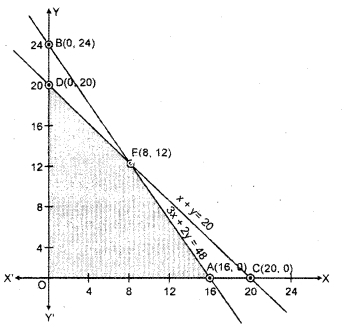
The coordinates of the comer points of this feasible region are O(0,0), A(16,0), E(8, 12) and D( 0,20) where E( 8,12) is the point of intersection of lines 3x + 2y = 48 and x + y = 20.
The value of objective function on these points are given in the following table:
| Point | x-coordinate | y-coordinate | Objective function Z = 22x + 18y |
| O | 0 | 0 | ZO = 22 x 0 + 18 x 0 = 0 |
| A | 16 | 0 | ZA = 22 x 16 + 18 x 0 = 352 |
| E | 8 | 12 | ZE = 22 x 8 + 18 x 12 = 392 |
| D | 0 | 20 | ZD = 22 x 0 + 18 x 20 = 360 |
From the table it is clear that the objective function has maximum value ₹392 at point E(8,12) where x = 8 and y = 12.
Hence dealer should purchase 8 fans and 12 sewing machines to get maximum profit ₹392.
Question 6.
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand opereated machines to manufacture a package of screw A, while it takes 6 minutes on automatic and 3 minutes on hand operated machines to manufacture a package of screw B. Each, machine is available for almost 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at ₹1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit ?
Solution:
Let manufacturer should produce x packets of screw of type A and y packets of screw of type B.
∴ Profit on x packets = ₹0-70x
and profit on y packets = ₹y
∴ Objective function to earn maximum profit
Z = 0.70 x + y
Time to produce x screws of type A = 4x minute
and time to produce y screws of type B = 6y minute
But automatic machine is available for 4 hours only.
∴ According to question.
4x + 6y ≤ 4 hour
⇒ 4x + 6y ≤ 240 minute
Similarly time taken to prepare screws of type A on handmade machine = 6x minutes
and time taken to prepare screws of type B on handmade machine = 3y minutes
But handmade machine is available for 4 hours only a day.
∴ 6x + 3y ≤ 4 hour
⇒ 6x + 3y ≤ 240 minute
∵ x and y are the number of screws.
∴ x ≥ 0 and y ≥ 0
Mathematically formulation of this Linear Programming Problem is as the following :
Maximize Z = 0.70x + y
Subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 0, y ≥ 0
Converting the given inequations into equations
4x + 6y = 240 …..(1)
6x + 3y = 240 …..(2)
Region represented by 4x + 6y ≤ 240 : The line 4x + 6y = 240 meets the coordinate axis at A(60, 0) and B(0, 40).
4x + 6y = 240
| X | 60 | 0 |
| y | 0 | 40 |
A(60, 0); B(0, 40)
Join the points A and 5 to obtain the line. Clearly (0, 0) satisfies the inequations 4 × 0 + 6 × 0 = 0 ≤ 240. So, the region containing the origin represents the solution set of the inequation.
Region represented by 6x + 3y ≤ 240 : The line 6x + 3y = 240 meets the coordinate axis at points C(40, 0) and D(0, 80).
6x + 3y = 240
| X | 40 | 0 |
| y | 0 | 80 |
C(40,0);D(0,80)
Join C and D to obtain the line.
Clearly (0,0) satisfies the given inequation 6 × 0 + 3 × 0 = 0 ≤ 240. So the region containing the origin represents the solution set of the inequation.
Region represented x ≥ 0 and y ≥ 0 : Since every point in the first quadrant satisfies these inequations.
So the first quadrant in the region represented by the inequation x ≥ 0 and y ≥ 0.
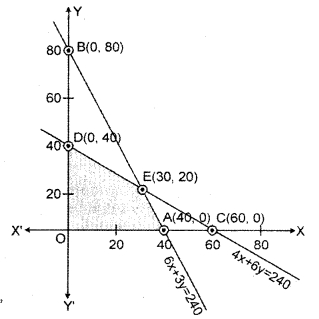
The coordinate of point of intersection of lines 4x + 6y = 240 and 6x + 3y = 240 are x = 30 and y = 20.
The shaded region OAED represent the common region of the inequations. This region is the feasible solution region of the inequations.
The comer points of this solution region are O(0,0), A(40, 0), E(30, 20) and D(0, 40).
The value of objective function on these points is as following table:
| Point | x-coordinate | y-coordinate | Objective function Z = 0.70 x + y |
| O | 0 | 0 | Z0 = 0.70 x 0 + 0 = 0 |
| A | 40 | 0 | ZA = 0.70 x 40 + 0 = 28 |
| E | 30 | 20 | ZE = 0.70 x 30 + 20 = 41 |
| D | 0 | 40 | ZD = 0.70 x 0 + 40 = 40 |
From the table the value of objective function is maximum at point E(30, 20) = ₹41.
Hence the manufacturer should produce 30 packets of screw of type A and 20 packets of screws of type B to get the maximum profit ₹41.
Question 7.
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of types A require 5 minute each for cutting and 10 minute each for assembling. Souvenirs of type B require 8 minute each for cutting and 8 minutes each for assembling. There are 3 hour 20 minute available for cutting and 4 hour available for assembling. The profit is ₹ 5 each for type A and ₹ 6 each for type B souvenirs. How many Souvenirs of each type should the company manufacture in order to maximize the profit ?
Solution:
Let company should make x souvenirs of type A and y souvenirs of type B.
Profit earned on x souvenirs = ₹ 5x and profit earned on y souvenirs = ₹ 6y
∴ To earn maximum profit, objective function is Z = 5x + 6y
∵ Time taken for cutting of souvenirs of type A = 5x minute
and time taken for cutting of souvenirs of type B = 8y minute
∴ According to question, constraints for total time taken for cutting
5x + 6y ≤ 3 hours 20 minute
⇒ 5x + 6y ≤ 200 minute
Similarly time taken for assembling of souvenirs of type A = 10x minute
and time taken for assembling of souvenirs of type B = 8y minutes
∴ According to question, constraints for total time taken in assembling
10x + 8y ≤ 4 hour
⇒ 10x + 8y ≤ 240 minute
Therefore mathematically formulation of Linear Programming Problem is as following :
Maximum Z = 5x + 6y
Subject to the constraints
5x + 8y ≤ 200
10x + 8y ≤ 240
x ≥ 0, y ≥ 0
Converting the given inequations into the equations.
5x + 8y = 200 …..(1)
10x + 8y = 240 …..(2)
Region represented by 5x + 8y ≤ 200: The line 5x + 8y = 200 meets the coordinate axis on ponits A(40, 0) and B(0, 25).
5x + 8y = 200
| X | 40 | 0 |
| y | 0 | 25 |
A(40, 0); B(0, 25)
Join A and D to obtain the line. Clearly (0, 0) satisfies the inequation 5(0) + 8(0) = 0 ≤ 200. So the region containing the origin represents the solution set of the inequation.
Region represented by 10x + 8y ≤ 240 : The line 10x + 8 y = 240 meets the coordinate axis at the points A(24,0) and B(0, 30).
10x + 8y = 240
| X | 24 | 0 |
| y | 0 | 30 |
C(24,0); D(0,30)
Join the points C and D to obtain the line. Clearly (0, 0) satisfies the given inequation 10(0) + 8(0) = 0 ≤ 240. So the region containing the origin represents the solution set of the inequation.
Region represented by x ≥ 0 and y ≥ 0 : Since every point in first quadrant satisfies the given inequation so the first quadrant is the solution region of these inequations x ≥ 0 and y ≥ 0.
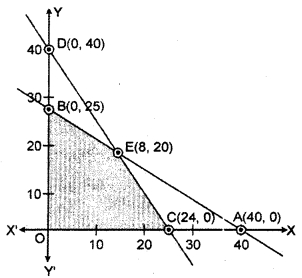
The coordinates of the point of intersection of lines 5x + 8y = 200 and 10x + 8y = 240 are x = 8 and y = 20.
The shaded region represents the common region of inequations. This region is the feasible solution of the linear programming problem.
The corner points of this region are O(0, 0), C(24, 0), E(8, 20) and B(0, 25).
The value of objective function on these points is shown in the following table :
| Point | x-coordinate | y-coordinate | Objective function Z = 5x + 6y |
| O | 0 | 0 | Z0 = 5 x 0 + 6 x 0 = 0 |
| C | 24 | 0 | Zc = 5 x 24+6 x 0 = 120 |
| E | 8 | 20 | ZE = 5 x 8 + 6 x 20 = 160 |
| B | 0 | 25 | ZB = 5 x 0 + 6 x 25 = 150 |
From the table objective function has the maximum value ₹160 at the point E(8, 20) where x = 8 and y = 20.
Question 8.
A Farmer has two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions a farmer find that he needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If F1 costs 60 paise/kg and F2 costs 40 paise/kg, determine how much of each type of fertilizer should be used so that nutrient requirements get a minimum cost.
Solution:
Let the quantity of fertilizers F1 = x kg and the quantity of fertilizers F2 = y kg.
∵ The cost of F1 is 60 paise per kg and the cost of F2 is 40 paise per kg.

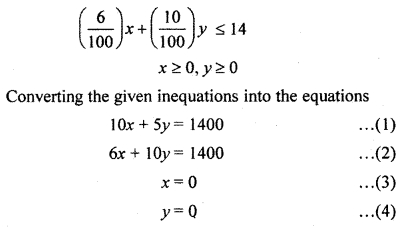
Region represented by (\(\frac { 10 }{ 100 } \))x + (\(\frac { 5 }{ 100 } \)) y ≤ 14: Line 10x + 5y = 1400 meets the coordinate axis at points ,A(140,0) and B(0, 280).
10x + 5y = 1400
| X | 140 | 0 |
| y | 0 | 280 |
A(140, 0); B(0, 280)
Join the points A to B to obtain the line. Clearly (0, 0) satisfies the given inequation
\(\frac { 10 }{ 100 } \) (0) + \(\frac { 5 }{ 100 } \) (0) = 0 ≤ 14
So the region containing origin represents the solution set of the inequation.
Region represented by (\(\frac { 6 }{ 100 } \))x + (\(\frac { 10 }{ 100 } \)) y ≤ 14: Line 6x + 10y = 1400 meets the coordinate axis at point C (\(\frac { 700 }{ 3 } \),0)and D(0, 140).
6x + 10y = 1400
| X | 700/3 | 0 |
| y | 0 | 140 |
C (\(\frac { 700 }{ 3 } \),0); and D(0,140)
Join C and D to obtain the line. Clearly (0, 0) satisfies the inequation 6(0) + 10(0) = 0 ? 1400. So the region containing origin represents the solution set of the inequation.
Region represented by x ≥ 0 and y ≥ 0 : Since every point in first quadrant satisfies the inequations. So the first quadrant is the solution region of the inequations x ≥ 0 and y ≥ 0.
Coordinates of the point of intersection of lines 10x + 5y = 1400 and 6x + 10y = 1400 are x = 100 and y = 80.
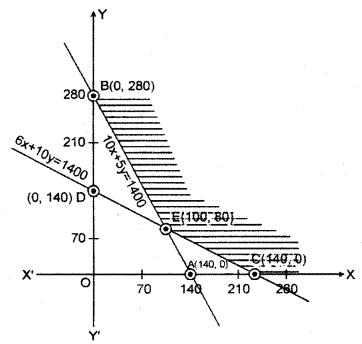
The shaded region CEB is the common region of the given inequations. This region is the feasible solution region of the inequations.
Corner points of this region are C (\(\frac { 700 }{ 3 } \),0) E (100 80) and B(0,280).
The value of objective function on these points are given in the following table :
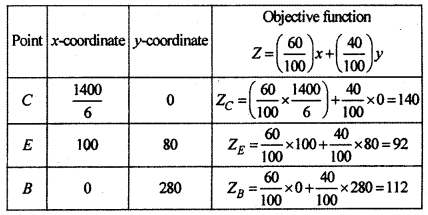
From the table, it is clear that objective function is minimum at E(100, 80). Hence the quantity of nutrients in F1 must be used 100 kg and in F2 it must be 80 kg and minimum value = ₹ 92.
Question 9.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost ₹ 25000 and ₹ 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than ₹70 lakhs and if his profit per unit on the desktop model is ₹4500 and on protable model is ₹5000.
Solution:
Let the number of desktop model = x and the number of portable model = y.
∴ Objective function to earn maximum profit
Z = 4500x + 5000y
Constraints for the total number of computers is
x + y ≤ 250
∵ monthly demand of computers is not more than 250.
Total cost of computers is
25000x + 40000y ? 70,000,00
∴ x and y are number of computers.
∴ x ≥ 0 and y ≥ 0
Mathematically formulation of Linear Programming Problem is as following :
Maximum Z = 4500x + 5000y
Subject to the constraints
x + y ≤ 250
25000x + 40,000y = 70,000,00
x ≥ 0 and y ≥ 0
Converting the given inequations, into the equations
x + y = 250 …..(1)
25000x + 40000y = 7000000
⇒ 25x + 40y = 7000 …..(2)
Region represented by x + y ≤ 250 : The line x + y = 250 meets the coordinate axis at the points A(250, 0) and B(0, 250).
x + y = 250
| X | 250 | 0 |
| y | 0 | 250 |
A(250, 0); B(0, 250)
Join point A to B to obtain the line. Clearly (0,0) satisfies the inequation 0 + 0 = 0 ≤ 250. So the region containing origin represents the solution set of the inequation.
Region represented by 25x + 40y ≤ 7000 : The line 25x + 40y = 7000 meets the coordinate axis on the points C(280, 0) and D(0, 175).
| X | 280 | 0 |
| y | 0 | 175 |
C(280, 0);D(0, 175)
Join point C to D to obtain the line. Clearly (0,0) satisfies the given inequation 25(0) + 40(0) = 0 ≤ 7000. So the region containing the origin represents the solution set of the inequation.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The coordinates of the point of intersection of lines x + y = 250 and 25x + 40y = 7000 are x = 200 and y = 50.
The shaded region OAED is the common region of the above inequations. This region is the feasible solution of the Linear Programming Problem.
The coordinates of the comer points of this region are O(0, 0), A(250, 0), E(200, 50) and D(0, 175).
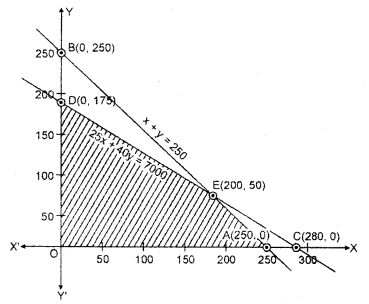
The value of objective function on these points is given in the following table :
| Point | x-coordinate | y-coordinate | Objective function Z = 4500x + 5000y |
| O | 0 | 0 | ZG = 4500 x 0 + 5000 x 0 = 0 |
| A | 250 | 0 | ZA = 4500 x 250 + 5000 x 0 = 11,25,000 |
| E | 200 | 50 | ZE = 4500 x 200 + 5000 x 50 = 900000 + 250000 = 1150000 |
| D | 0 | 175 | ZD = 4500 x 0 + 5000 x 175 = 8,75000 |
It is clear from the table that the objective function value is maximum at point E(200, 50)
and z = 11,50,000
So the merchant should purchase 200 desktop computer and 50 portable computer to earn maximum profit of ?11,50,000.
Question 10.
Two godowns A and B have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transporation per quintal from the godowns to the shop are given in the following table :
| To/From | A | B |
| D | 6 | 4 |
| E | 3 | 2 |
| F | 2.50 | 3 |
How should the supplies be transported in order that the transportation cost is minimum ?
Solution:
Let store A supplies x quintals to shop D and y quintals to shop E.
∴ remaining ration (100 – x – y) quintal will be supplied to shop F.
∴ Transporation charges from store A to shop D = ₹ 6x
and transportation charges from store A to shop E = ₹ 3y
and transportation charges from store A to shop E
= ₹ \(\frac { 5 }{ 2 } \) (100 – x – y)
∴ Total transportation charges from store A to shops D,
E and F = 6x + 3y + \(\frac { 5 }{ 2 } \) (100 – x – y).
The remaining requirement of shop D = (60 -x) quintal
The remaining requirements of shop E = (50 – y) quintal
and the remaining requirement of shop F
= [40 – (100 – x – y)] quintal
which will be supplied from store B.
∴ Transportation charges from store B to shop D = ₹ 4 (60 – x).
Transportation charges from store B to shop E = ₹2 (50 – y)
and transportation charges from store B to shop F = ₹ 3(x + y – 60)
∴ Total trapsortation charges from store B to shops D, E and F = 4(60 – x) + 2(50 – y) + 3(x + y – 60).
∴ Total transportation charges from both stores A and B to the shops D, E and F.
Z = 6x + 3y + \(\frac { 5 }{ 2 } \) (100 – x – y) + 4(60 – x) + 2(50 – y) + 3(x + y – 60)
= 2.5x + 1.5y + 410
Total capacity of stored = 100 quintal.
∴ x + y ≤ 100
Ration availed by shop D is x quintal from store A and remaining from store B.
∴ x ≤ 60
Similarly shop E avails y quintal from store A and remaining from store B.
∴ y ≤ 50
Similarly shop F avails (100 – x – y) quintals from store A and remaining from store B.
∴ x + y ≥ 60
∵ x and y are quantity of ration in quintal.
∴ x ≥ 0 and y ≥ 0
So mathematical formulation of Linear Programming Probelm is as following :
Z = 2.5x + 1.5y + 410
x + y ≤ 100
x ≤ 60
y ≤ 50
x + y ≥ 60
x ≥ 0, y ≥ 0
Converting these inequations into the equations
x + y = 100 …..(1)
x = 60 …..(2)
y = 50 …..(3)
x + y = 60 …..(4)
x = 0 …..(5)
y = 0 …..(6)
Region represented by x + y ≤ 100 : Line x + y = 100 meets the coordinate axis on points A(100,0) and B(0,100).
x + y = 100
| X | 100 | 0 |
| y | 0 | 100 |
A( 100, 0); B(0, 100)
Join points A to B to obtain the line. Clearly (0,0) satisfies the inequation 0 + 0 = 0 ≤ 100. So the region containing the origin represents the solution set of the inequation.
Region represented by x ≤ 60 : Line x = 60 is parallal toy-axis and its each point will satisfy the inequation in first quadrent so its solution region will be towards origin.
Region represented by y ≤ 50 : Line y = 50 is parallel to x-axis and its each point will satisfy the inequation in first quadrant. So. its solution region will be towards origin.
Region represented by x + y ≥ 60: Line x + y = 60 meets the coordinate axis on the points G(60, 0) and H(0, 60).
x + y = 60
| X | 60 | 0 |
| y | 0 | 60 |
G(60, 0); H(0, 60)
Join G and H to obtain the line. Clearly the origin (0,0) does not satisfying the inequation so the region of solution set is opposite to the origin.
Region represented by x ≥ 0 and y ≥ 0 : Since every point in first quadrant satisfies the inequations x ≥ 0 and y ≥ 0 so the solution set of these inequations is in the first quadrant.
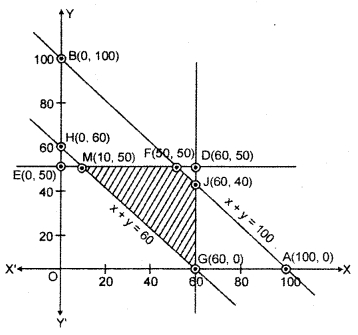
The shaded region GJFM is the common region representing the inequations. This region is the feasible solution region of the inequations.
Coordinates of comer points of this region are G(60,0), J(60,40), F(50,50) and M(10, 50) where point J is the point of intersection of lines x + y = 100 and x = 60, point F is the point of intersection of x + y = 100 and y = 50 and M is the point of intersection of x + y = 60 and y = 50.
The value of objective function on these points is given in following table :
| Point | x-coordinate | y-coordinate | Objective function Z = 2.5x + 1.5y + 410 |
| G | 60 | 0 | ZG = 2.5(60) + 1.5(0) + 410 = 560 |
| J | 60 | 40 | Zj = 2.5(40) + 1.5(40) + 410 = 620 |
| F | 50 | 50 | ZF = 2.5(50) + 1.5(50) + 410 = 610 |
| M | 10 | 50 | ZM = 2.5(10) + 1.5(50) + 410 = 510 |
It is clear from the table the objective function has minimum value Z = ₹ 510 at the point M(10,50).
Hence for minimum transportation charges merchant should supply the ration from store A to shops D, E and F as 10,50 and 40 quintals respectively and from store B to shops D, E and F as 50,0,0 quintal respectively.