Rajasthan Board RBSE Class 12 Maths Chapter 16 Probability and Probability Distribution Ex 16.2
Question 1.
If A and B be two events such that P(A) = \(\frac { 1 }{ 4 }\); = P(B) = \(\frac { 1 }{ 2 }\) and P(A ∩ B)
= \(\frac { 1 }{ 8 }\), then find \(P(\overline { A } \cap \overline { B } )\).
(1 – P(A)] = P(B) PĀ) = P(Ā)P(B)
Solution:
Given:
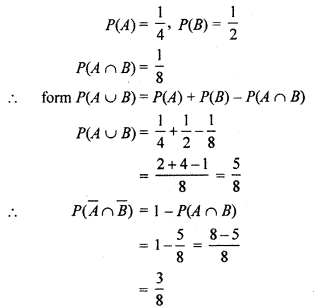
Question 2.
If P(A) = 0.4, P(B) = p and P(A ∪ B) = 0.6 and A and B are independent events, then find the value of p.
Solution:
Given P(A) = 0.4
P(B) = p
P(A ∩ B) = 0.6
∵ A and B are independent events
So, P(A ∩ B) = P(A). P(B)
P(A ∪ B) = P(A) + P(B) – P(A ∩B)
⇒ 0.6 = 0.4 x p – P(A)P(B)
0.6 = 0.4 x p – 0.4 x p
0.2 = 0.6 x p
P = \(\frac { 0.2 }{ 0.6 }\) = \(\frac { 1 }{ 3 }\)
Hence, p = \(\frac { 1 }{ 3 }\).
Question 3.
If A and B are independent events, and P(A) = 0.3, P(B) = 0.4, then find:
(i)P(A ∩ B)
(ii)P(A ∪ B)
(iii) P(\(\frac { A }{ B }\))
(iv) P(\(\frac { B }{ A }\))
Solution :
(i) Given :
P(A) = 0.3
P(B) = 0.4
A and B are independent events
P( A ∩ B) = P(A) · P(B)
= 0.3 x 0.4 = 0.12
(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.3 + 0.4 – 0.12
= 0.7 – 0.12 = 0.58
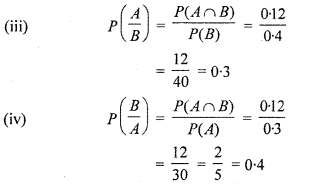
Question 4.
If A and B are independent events., where P(A) = 0.3, P(B) = 0.6, then find:
(i)P(A ∩ B)
(ii) P(A ∪\(\overline { B }\))
(iii) P(A ∪ B)
(iv) P(\(\overline { A }\) ∩\(\overline { B }\))
Solution :
Given
P(A) = 0.3
P(B) = 0.6
(i) P(A ∩ B) = P(A) × P(B)
= 0.3 × 0.6
= 0.18
(ii) P(A ∪ \(\overline { B }\))
= 0.3 – 0.18
= 0.12
(iii) P(A ∪ B) = p(A) + P(B) – P(A ∩B)
= 0.3 + 0.6 – 0.18
= 0.90 – 0.18
(iv) P(\(\overline { A }\) ∩ \(\overline { B }\))
= [ 1 – P(A)] [1 – P(B)]
= [1 – 0.3] [1 – 0.6]
= 0. 7 × 0.4
= 0.28
Question 5.
A bag contains 5 white, 7 red and 8 black balls. If four balls are drawn one by one without replacement, find the probability of getting all white balls.
Solution:
Given
White ball = 5
Red ball = 7
Black ball = 8
Total number of balls = 5 + 7 + 8 = 20
∴ Probability of getting first white ball
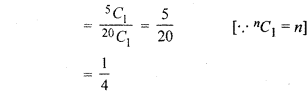
Probability of getting second white ball
![]()
Probability of getting third white ball
![]()
Probability of getting fourth white ball
![]()
Probability of getting all white balls
![]()
Question 6.
A die is tossed thrice. Find the probability of getting an odd number at least once.
Solution:
Number of possible results on a die = {1, 2, 3, 4, 5, 6}
∴ Number of favourable results getting even number (2, 4, 6) = 3
∴ Probability of getting even number = \(\frac { 3 }{ 6 }\) = \(\frac { 1 }{ 2 }\)
∴ Probability of getting even number once = \(\frac { 1 }{ 2 }\)
∴ Probability of getting even number thrice = \(\frac { 1 }{ 2 } \times \frac { 1 }{ 2 } \times \frac { 1 }{ 2 } =\frac { 1 }{ 8 }\)
∴ Probability of getting at least one odd number on tossing all dice together
= 1 – \(\frac { 1 }{ 8 }\) = \(\frac { 7 }{ 8 }\)
Question 7.
Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
Solution:
Number of black cards in a pack= 26
Total number of cards = 52
∴ Probability of getting one black card =
![]()
After drawing one black card, remaining cards are 51.
Out of them number of black cards = 25
∴ Probability of getting other black card =
![]()
∴Probability of getting both black cards
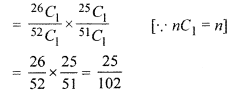
Question 8.
Two coins are tossed. What is the probability of coming up two heads if it is known that at least one head comes up ?
Solution:
Possible ways of tossing two coins {HH, HT, TH, TT} = 4
Number of ways where at least one head comes up 4 – 1 = 3
Number of getting both heads = 1
∴Probability of getting both heads = \(\frac { 1 }{ 3 }\)
Hence, requried probability = \(\frac { 1 }{ 3 }\)
Question 9.
In a hostel, 60% of the students read Hindi newspaper, 40% read English newspaper and 20% read both Hindi and English newspapers. A student is selected at random :
(i) find the probability that he reads neither Hindi nor English newspapers.
(ii) If he reads Hindi newspaper, find the probability that he reads English newspaper.
(iii) If he reads English newspaper. Find the probability that he reads Hindi newspaper.
Solution:
(i) Let
H: Event of reading Hindi newspaper
and E: Event of reading English newspaper
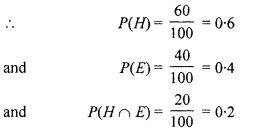
Probability of reading at least one newspaper is
= P(H ∪ E)
P(H ∪ E) = P(H) + P(E) – P(H ∩ E)
= 0.6 + O.4 – 0.2
= 0.8
Therefore probability of reading neither Hindi nor English newspaper by students
= 1 – P(H ∪ E)
= 1 – 0.8
= 0.2 = 20%
Clearly 20% students do not read newspaper.
∴ Required probability = \(\frac { 20 }{ 100 }\) = \(\frac { 1 }{ 5 }\)
(ii) If student read Hindi newspaper English
∴ Probability of reading English newspaper also
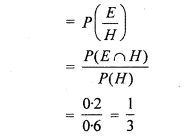
(iii) If student reads English newspaper, then probability of reading Hindi newspaper also
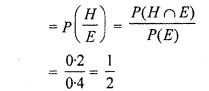
Question 10.
A can solve 90% of the problems given in a book and B can solve 70%. What is the probability that at least one of them will solve the problem, selected at random from the book ?
Solution :
Let
P(A) = \(\frac { 90 }{ 100 }\); P(B) = \(\frac { 70 }{ 100 }\)
∴ Probability of at least solving by one
= P(\(\overline { A }\)B) + P(A\(\overline { B }\)) + P(AB)
= P(\(\overline { A }\)) x P(B) + P(\(\overline { A }\))P(\(\overline { B }\)) + P(A)x P(B)
= [1 – P(A)] x P(B) + P(A) [1 – P(B)] + P(A) x P(B)]
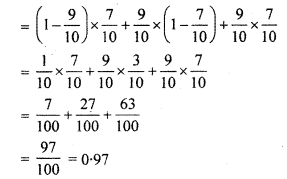
Question 11.
A problem in mathematics is given to 3 students whose chances of solving it are \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 3 }\)and \(\frac { 1 }{ 4 }\) What is the probability that the problem is solved ?
Solution:
Problem will be solved if at least one student can solve.
∴ Probability of solving by one student = \(\frac { 1 }{ 2 }\)
= 1 – \(\frac { 1 }{ 2 }\) = \(\frac { 1 }{ 2 }\)
Probability of not solving by any student = 1 – \(\frac { 1 }{ 3 }\) = \(\frac { 2 }{ 3 }\)
Similarly, probability of not solving by third student = 1 – \(\frac { 1 }{ 4 }\) = \(\frac { 3 }{ 4 }\)
Probability of not solving by any one of them = \(\frac { 1 }{ 2 }\) x \(\frac { 2 }{ 3 }\) x \(\frac { 3 }{ 4 }\) = \(\frac { 1 }{ 4 }\)
∴ Probability of solving by at least one of them = 1 – \(\frac { 1 }{ 4 }\) = \(\frac { 3 }{ 4 }\)
Question 12.
A bag contains 5 white and 3 black balls. Four balls are successively drawn out without replacement. What is the probability that they are alternately of different colours ?
Solution:
Total number of balls = 5 + 3 = 8
∴Probability of getting one white ball = \(\frac { 5 }{ 8 }\)
∴ Number of remaining balls = 8 – 1 = 7
out of them there are 4 white and 3 black balls.
∴ Probability of being black ball = \(\frac { 3 }{ 7 }\)
Number of remaining balls 7 – 1 = 6 where are 4 white and 2 black balls
∴ Probability of being third white ball = \(\frac { 4 }{ 6 }\)
Number of remaining balls = 6 – 1= 5,
where are 3 white and 2 black
∴Probability of being fourth black ball = \(\frac { 2 }{ 5 }\)
∵Events are independent every time
∴ Probability of being different colours ball
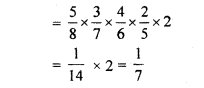
Question 13.
Probabilities of solving a specific problem independently by A and B are \(\frac { 1 }{ 2 }\), and \(\frac { 1 }{ 3 }\) respectively. If both try to solve the problem independently, find the probability that
(i) the problem is solved,
(ii) exactly one of them solves the problem.
Solution:
(i) Probability of solving the problem by A = P(A) = \(\frac { 1 }{ 2 }\)
⇒ Probability of not solving the problem by A
P(\(\overline { A }\)) = 1 – P(A)
= 1 – \(\frac { 1 }{ 2 }\) = \(\frac { 1 }{ 2 }\)
Probability of solving the problem by B.
P(B) = \(\frac { 1 }{ 3 }\)
⇒ Probability of not solving the problem by B.
P(\(\overline { B }\)) = 1 – P(B)
= 1 – \(\frac { 1 }{ 3 }\) = \(\frac { 2 }{ 3 }\)
∴ Probability that problem not is solved
P(\(\overline { A }\).\(\overline { B }\)) = P(\(\overline { A }\)).P(\(\overline { B }\))
= \(\frac { 1 }{ 2 }\) x \(\frac { 2 }{ 3 }\) = \(\frac { 1 }{ 3 }\)
⇒ Probability that problem is solved
= 1 – P(\(\overline { AB }\))
= 1 – \(\frac { 1 }{ 3 }\) = \(\frac { 2 }{ 3 }\)
(ii) A and B are independent problems.
Here P(A) = \(\frac { 1 }{ 2 }\) , P(\(\overline { B }\)) = \(\frac { 2 }{ 3 }\)
P(\(\overline { A }\)) = \(\frac { 1 }{ 2 }\) , P(B) = \(\frac { 1 }{ 3 }\)
∴ Probability that exactly one of them solves the problem
= P(A\(\overline { B }\)) + P(\(\overline { A }\)B)
= P(A).P(\(\overline { B }\)) + P(\(\overline { A }\)).P(B)
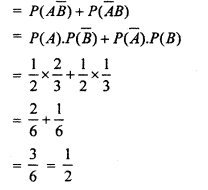
RBSE Solutions for Class 12 Maths