RBSE Solutions for Class 12 Maths Chapter 16 Probability and Probability Distribution Ex 16.3

Rajasthan Board RBSE Class 12 Maths Chapter 16 Probability and Probability Distribution Ex 16.3

Question 1.
Given there are two bags I and II. Bag I contains 3 red and 4 black bails while another bag II contains S red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from bag II.
Solution:
Let E₁ be the event that the ball is drawn from the bag I and II and E₂ be the event that it is drawn from the bag II and E be the event that the drawn ball is red.
Since the drawn ball is found to be red, so we have to Find P(\(\frac { { E }_{ 2 } }{ A } \)) the probability of drawing red ball from bag II. since both the bags are equally likely to be selected to draw the ball, we have

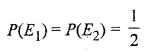
Probability of getting red ball from bag I

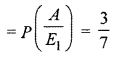
Probability of getting red ball from bag II

Probability of getting red ball from bag III

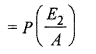
Hence, using Baye’s Theorem,

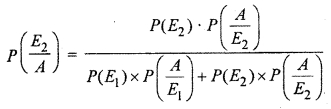
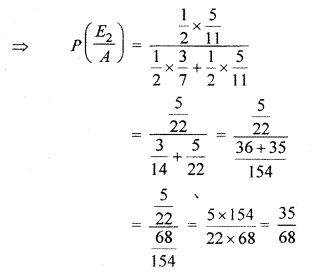
Question 2.
A doctor has to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter or by other means of transport are respectively \(\frac { 3 }{ 10 } \),\(\frac { 1 }{ 5 } \),\(\frac { 1 }{ 10 } \) and \(\frac { 2 }{ 5 } \). The probabilities that he will be late are \(\frac { 1 }{ 4 } \),\(\frac { 1 }{ 3 } \) and \(\frac { 1 }{ 12 } \), if he comes by train, bus and scooter respectively, but if he comes by other means of transport, than he will not be late. When he arrives, he is late. What is the probability that he comes by train ?
Solution:
Let E be the event “Doctor comes late to visit a patient” and if Doctor comes by Train, Bus, Scooter and any-other means, then probabilities are T₁, T₂, T₃ and T₄ respectively.

Question 3.
Bag I contains 3 red and 5 black balls and by II contains 4 red and 5 black balls. One ball transferred from bag I to bag II and then a ball is drawn from bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black.
Solution:
Bag I contain 3 red and 4 black balls, and Bag II contains 4 red and 5 black balls.
Let, E₁ = Event of drawing red ball from bag I
and E₂ = Event of drawing black ball from bag II
and A : Event of drawing red ball after transfering one ball from I to II

Question 4.
A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls, One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.
Solution:
Let E₁ is the event of drawing from bag I
and E₂ of drawing from bag II
and A represent the event of drawing red ball.
∴ Probability of chosing one bag = \(\frac { 1 }{ 2 } \)
Or P(E₁) = P(E₂) = \(\frac { 1 }{ 2 } \)
There are 4 red and 4 black balls in bag I.
∴ Probability of drawing red ball from it

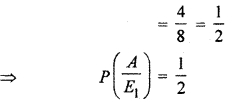
In second bag, there are 2 red and 6 black balls.
∴ Probability of drawing red ball from it

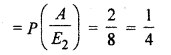
Now probability of drawing red ball from first bag

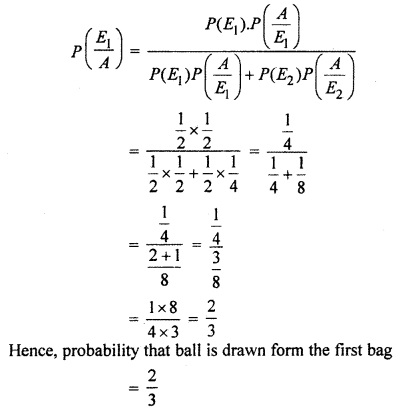
Question 5.
There are three coins. One is having head on both faces, another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin ?
Solution:
Probability of selecting one coin out of three = \(\frac { 1 }{ 3 } \)
E₁ : event that coin having head on both faces.
E₂ : event that coin is biased that head come up 75% of the time.
E₃ : event that third is a unbiased,
and A is the event of getting head

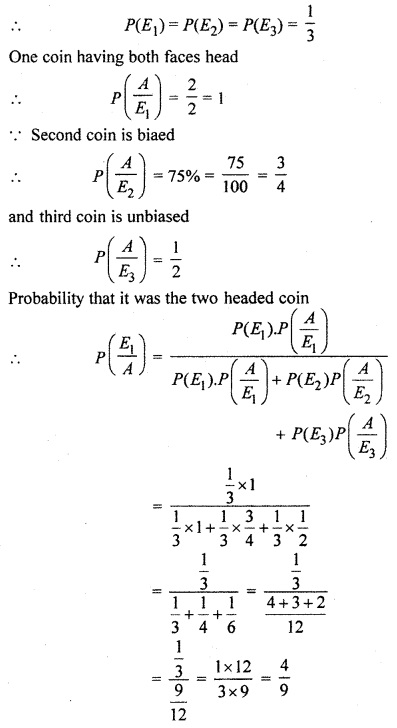
Hence, required probability = \(\frac { 4 }{ 9 } \)

Question 6.
A laboratory blood test is 99% effective in detecting a certain disease when it is if fact, present. However, the test also yields a false positive result for 0-5% of the healthy person tested. If 0.1 percent of the population actually has the disease. What is the probability that a person has the disease given that his test result is positive ?
Solution:
Let E₁ : Event that patient is effected from desease.
E₂ = Event that patient is not effected from desease and A be the event that blood is tested.
∴ Probability of the person effected from disease

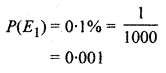
Probability of the person not affected from disease

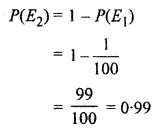
Probability of those who are patient and their blood are tested

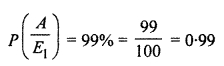
Probability of those who were tested but not patient

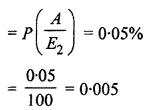
∴ Probability that a person has the disease given that his test is positive

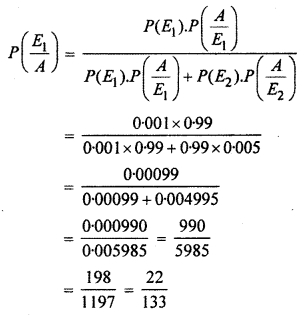
Hence, the required probability = \(\frac { 22 }{ 133 } \)

Question 7.
Of the sutdents in a college, it is known that 60% reside in hostel and 40% are day scholars. Previous year result report that 30% of all student who reside in hostel attain, A grade and 20% of day schloars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has on A grade, what is the probability that the student is a hostlier ?
Solution:
Solution : Let E₁ : Event that students reside in hostel and E₂ : Event that students do not reside in hostel
∴ Probability of students reside in hostel

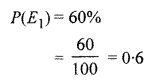
Probability that students do not reside in hostel

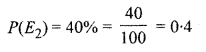
Probability of students securing grade A who reside in hostel

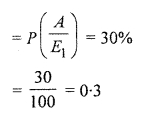
Probability of students who do not reside in hostel but. secure grade A

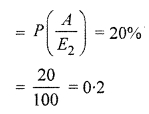
∴ Probability that student securing graded is a hostelier = P (\(\frac { { E }_{ 1 } }{ A } \))

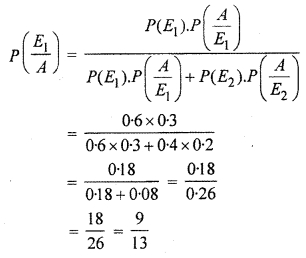
Hence, required probability : \(\frac { 9 }{ 13 } \)

Question 8.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probabilities of an accident are 0-01, 0*03 and 0-15 respectively. One of the insured person meets with an accident. What is the probability that he is a scooter driver ?
Solution:
Let E₁ : Event that scooter driver is insured
E₂ = Event that car driver is insured
E₃ = Event that truck driver is insured
and A : Even that an accident occurs.
A company insured 2000 scotter drivers, 4000 car drivers and 6000 truck drivers.
∴ Total number of drivers insured = 2000 + 4000 + 6000 = 12000
∴ Probability of scooter drivers insured

Probability of car drivers insured

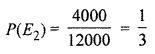
Probability of truck drivers insured

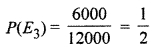
Probability of scooter drivers accidents

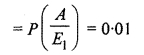
Probability of car drivers accidents

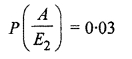
Probability of truck drivers accidents

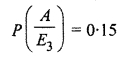
A person meets an accident who is insured.
∴ Probability that the persons is a scooter driver

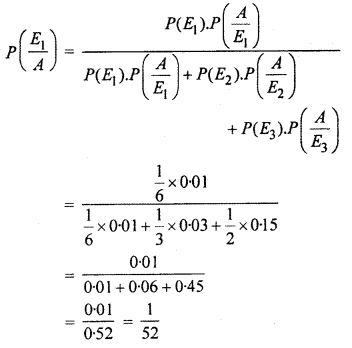
Hence, required probability : \(\frac { 1 }{ 52 } \)

Question 9.
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let \(\frac { 3 }{ 4 } \) be probability that he knows the answer and \(\frac { 1 }{ 4 } \) be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability \(\frac { 1 }{ 4 } \). What is the probability that the student knows the answer given that he answered it correctly ?
Solution:
Let E₁ : Event that student knows the answer
E₂ : Event that student guesses
and A : Event that he answers correctly

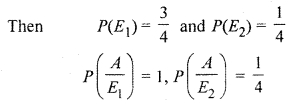
∴ Probability that he answers correctly

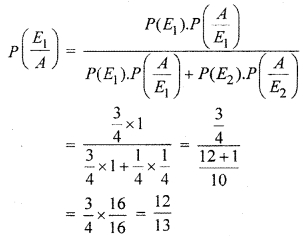
Hence requried Probability = \(\frac { 12 }{ 13 } \)

Question 10.
Suppose 5% men and 0.25% women has white hairs. A person with white hair is chosen at random. Find the probability that a male is selected. Assume that there are equal number of men and women.
Solution:
Given that number of men and women are equal
Let events E₁ = To be a man
E₂ = To be a woman
A = White hair

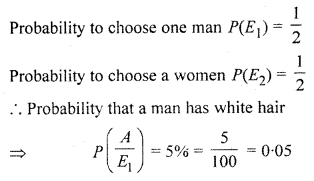
Question 11.
Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducting a new product is 0.7 and the corresponding probability is 0-3 if the second group wins. Find the probability that the new product introduced was by the second group.
Solution:
Let events
E₁ : First group wins, introduce new product.
E₂ : Second group wins, introduce new product.
Given : Probability that first group wins = P(E₁) = 0.6
Probability that second group wins = P(E₂) = 0.4
Probability that first group wins introducting new product,

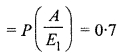
Probability that second group wins introducting new product

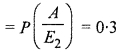
∴ Probability that new product introduced was by the second group

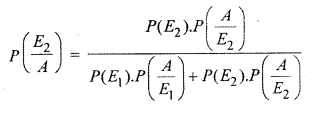
Question 12.
Suppose a girl throw a dice. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1,2,3 or 4 then tosses a coin once and notes whether a head or tall is obtained. If she obtained exactly one head, what is the probability that she threw 1,2,3 or 4 with the die ?
Solution:
Number of possible results after throwing a die = (1,2, 3, 4, 5, 6) = 6
Let E₁ : Event she gets 5 or 6
E₂ : Event she gets 1, 2, 3, 4
A : Event that she gets head if tosses a coin
∴ Probability that 5 or 6 acheived

Probability that 1, 2, 3,4 are acheived

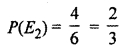
If she gets 5 or 6 she tosses a coin thrice and notes the number of heads.
(HHH, HHT, HTH, THH, HIT, THT, TTH, TIT)
∴ Number of ways to get one head = (HTT, THT, TTH) = 3
∴ Probability to get one head = \(\frac { 3 }{ 8 } \)

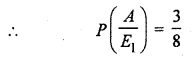
If she gets 1, 2, 3, 4, then she tosses a coin once and notes whether a head or tail.
∴ Probability to get one head = \(\frac { 1 }{ 2 } \)

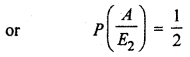
If she obtained exactly one head, than probability that she threw 1,2, 3 or 4

Question 13.
A card from a pack of 52 card is lost From remaining cards of the pack, two cards are drawn found to be both diamonds. Find probability of the lost card being a diamond.
Solution:
Let Events E₁ = Lost card is diamond
E₂ = Lost card is not diamond
The number of diamond card = 13 out of 52 cards.

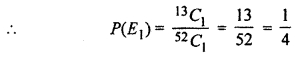
and 39 cards are not diamonds

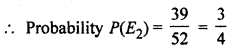
(i) When a card of diamond lost there remaining cards of diamond are 12 out of 52.

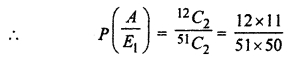
Here A represents the cards lost.
(ii) When diamonond card is not
Lost then probability of drawing 2 cards of diamond

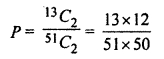
∴ Probability that lost card is a diamond


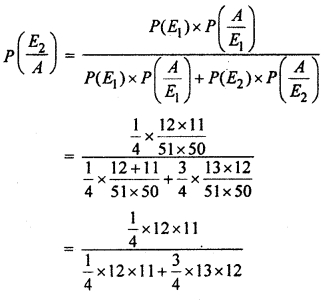
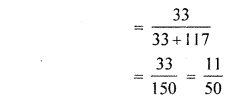
Hence, required probability = \(\frac { 11 }{ 50 } \)

Question 14.
A bag contains 3 red and 7 black. Two balls are drawn one by one at a time at random without replacement. If second drawn half is red, then what is the probability that first drawn ball is also red ?
Solution:
A = Event that drawn ball is Red first time.
and B = Event that drawn ball is also red in second time.
Then P(A ∩ B) = P( 1 red and 1 red)

RBSE Solutions for Class 12 Maths