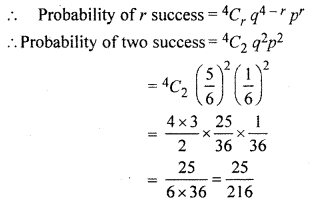Rajasthan Board RBSE Class 12 Maths Chapter 16 Probability and Probability Distribution Ex 16.5
Question 1.
If a fair coin is tossed 10 times, then find the probabilities of the following;
(i) exactly 6 heads ?
(ii) atleast 6 heads ?
(iii) atmost 6 heads ?
Solution:
(i) A fair coin is tossed 10 times and X = numbers of heads.
∴ In distribution X, n = 10 and p = probability of head = \(\frac { 1 }{ 2 } \)

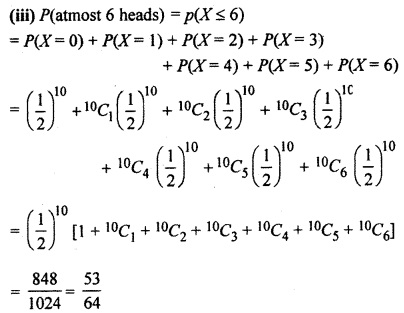
Question 2.
An urn contains 5 white, 7 red and 8 black balls. If 4 balls are drawn one by one with replacement, what is the probability that:
(i) all are white
(ii) only 3 are white
(iii) none is white
(iv) at least 3 are white
Solution:
(i) Total number of balls
= 5 + 7 + 8 = 20
Number of white balls = 5
Probability of getting white ball is one chance = \(\frac { 5 }{ 20 } \) = \(\frac { 1 }{ 4 } \)
∵ All events are independent
∴ Required probability = \(\frac { 1 }{ 4 } \) × \(\frac { 1 }{ 4 } \) × \(\frac { 1 }{ 4 } \) × \(\frac { 1 }{ 4 } \) = (\(\frac { 1 }{ 4 } \))4
(ii) Probability of drawing white ball first time
= 3C1 × \(\frac { 1 }{ 4 } \) × \(\frac { 1 }{ 4 } \) × \(\frac { 1 }{ 4 } \)
= 3 ×(\(\frac { 1 }{ 4 } \))3
(iii) P(no ball is white)
∴ Number of other balls = 7 + 8 = 15
∴ Probability of drawing one other colour ball = \(\frac { 15 }{ 20 } \) = \(\frac { 3 }{ 4 } \)
∴ Probability of other colour balls drawn successively (none is white)
= \(\frac { 3 }{ 4 } \) × \(\frac { 3 }{ 4 } \) × \(\frac { 3 }{ 4 } \) × \(\frac { 3 }{ 4 } \)
= (\(\frac { 3 }{ 4 } \))4
(iv) P(at least 3 white) = P (four white) + P(three white)
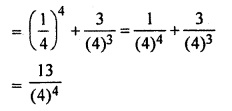
Question 3.
In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is \(\frac { 5 }{ 6 } \). What is the probability that he will knock down fewer than 2 hurdles ?
Solution :
Number of total hurdles (n) = 10
Probability of clearing the hurdles = P = \(\frac { 5 }{ 6 } \)
∴ Probability of non clearing the hurdles

Question 4.
five dices are thrown simultaneously. If the occurrence of an even number in a single dice is considered a success, find the probability of at most 3 success.
Solution:
Sample space on throwing a dice s = {1,2, 3,4, 5,6}
∴ n(S) = 6
Let A represents even numbers
∴A = {2,4,6}
n(A) = 3
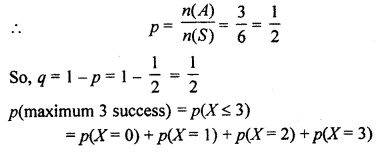
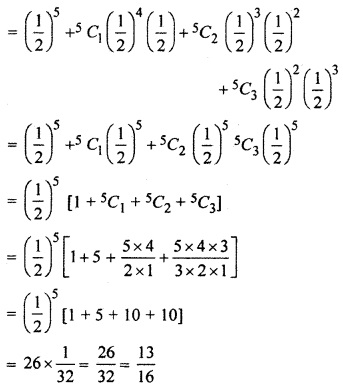
Question 5.
Ten eggs are drawn successively, with replace¬ment, from a lot containing 10% defective eggs. Find the probability that there is at least one defective egg.
Solution:
Probability of defective eggs = 10%

Question 6.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \(\frac { 1 }{ 100 } \) What is the probability that he will win a prize.
(i) at least once
(ii) exactly once
(iii) at least twice
Solution:


Question 7.
The probability that a bulb produced by a factory will fuse after 150 days on use is 0*05. Find the probability that out of 5 such bulbs
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.
Solution:
Probability that a bulb will fuse after 150 days p = 0.05
Probability that bulb will not fuse after 150 days q = 1 – p = 1 – 0.05 = 0.95
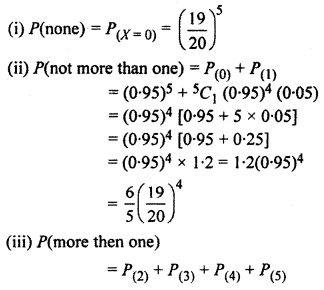
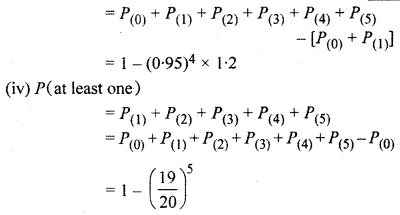
Question 8.
In a multiple choice examination with three possible answers for each of the 5 questions out of which only one is correct. What is the probability that a candidate would get four or more correct answers just by guessing ?
Solution:
∵ One answer is correct out of 3
∴ Probability of correct answer = p = \(\frac { 1 }{ 3 } \)
∴ Probability of wrong answer
= q = 1 – p
= 1 – \(\frac { 1 }{ 3 } \) = \(\frac { 2 }{ 3 } \)
Probability that 4 or more answers are correct
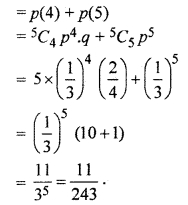
Question 9.
In a 20 questions true-false examination are asked. Suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, his answer ‘true’ If it falls tails, his answer ‘false’. Find the probability that his answer at least 12 questions correctly.
Solution:
P (Getting head on toss) P = \(\frac { 1 }{ 2 } \)
P (not getting head on toss)
q = 1 – person
= 1 – \(\frac { 1 }{ 2 } \) = \(\frac { 1 }{ 2 } \)
∴ Probability of writing correct answer = \(\frac { 1 }{ 2 } \)
and probability of writing incorrect answer = \(\frac { 1 }{ 2 } \)

Question 10.
A bag contains 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0 ?
Solution:
A bag contains 10 balls each marked with one of the digit from 0 to 9.
Probability that one ball is in marked 0 drawn
P = \(\frac { 1 }{ 10 } \) = 0.1 = 0.1
Probability that ball is not marked 0
q = 1 – p
= 1 – 0.1 = 0.9
Now 4 balls are drawn successively with replacement.
∴ Probability that any of them ball is marked 0
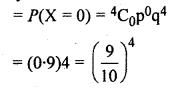
Question 11.
Five cards are drawn successively with replacement from a well shuffled pack of 52 cards. What is the probability that:
(i) all the five cards are spades ?
(ii) only 3 cards are spades ?
(iii) none is spade ?
Solution:
There are 13 cards are spade out of all 52 cards. Probability of drawing one card of spade
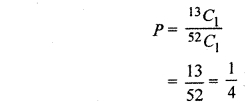

Question 12.
Suppose X has a binomial distribution B(6,\(\frac { 1 }{ 2 } \)). Show that x = 3 is the most likely outcome.
Solution:
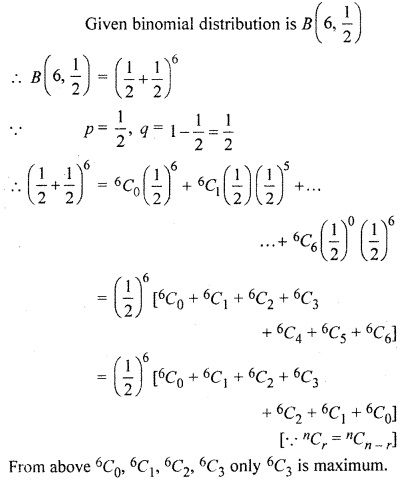
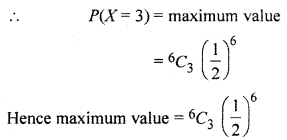
Question 13.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two success.
Solution:
When a pair of dice in thrown
∴ Number of all possible outcomes
n(S) = 6 × 6 = 36
Number of doublets can be make from a pair of dice = 6
[(1,1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)]
∴ Probability that doublet are find
P = \(\frac { 6 }{ 36 } \) = \(\frac { 1 }{ 6 } \)
and probability that doublets are not find
q = 1 – p
= 1 – \(\frac { 1 }{ 6 } \) = \(\frac { 5 }{ 6 } \)
A pair of dice is thrown four times
∴ n = 4