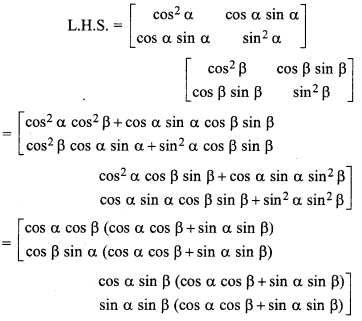RBSE Solutions for Class 12 Maths Chapter 3 Matrix Miscellaneous Exercise

Rajasthan Board RBSE Class 12 Maths Chapter 3 Matrix Miscellaneous Exercise

RBSE Solutions For Class 12 Maths Chapter 3 Miscellaneous Question 1.
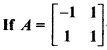, then find A.
Solution:

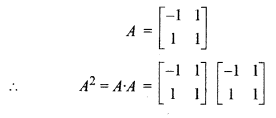
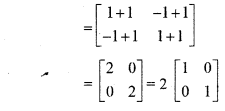
RBSE Solutions For Class 12 Maths Chapter 3 Question 2.
, then find (A – 2I) (A – 3I).
Solution:

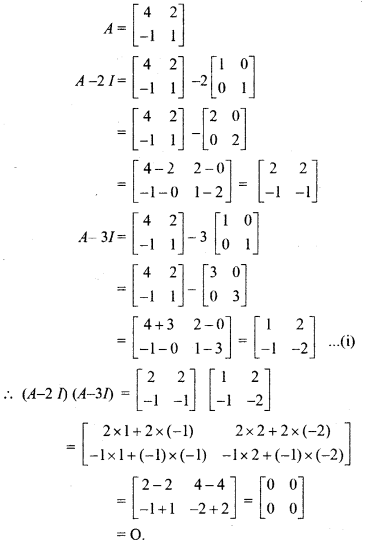
RBSE Solution Class 12 Maths Chapter 3 Question 3.
, then find AB.
Solution:

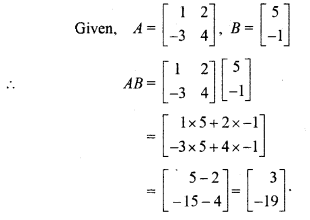
RBSE 12th Maths Chapter 3 Question 4.
, then find BA.
Solution:

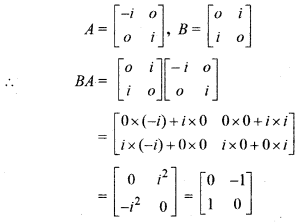
RBSE Solutions For Class 10 Maths Chapter 3 Miscellaneous Question 5.
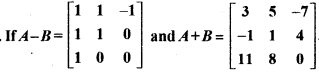, then find matrices A and B.
Solution:

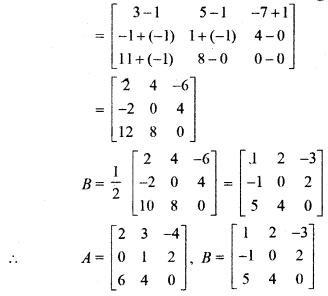
Miscellaneous Exercise Chapter 3 Class 12 Question 6.
, then find the value of x and y.
Solution:
On comparing,
x + 2 = -2 ∴ x = -4
– y – 2 = 5 ⇒ y = -7

Hence, x = -4, y = -7

Class 12 Maths Chapter 3 Miscellaneous Exercise Solutions Question 7.
Order of matrix A is 3 x 4 and B is a matrix, such that A^TB and AB^T defined, then write the order of B.
Solution:
∴ Order of A = 3 x 4
∴ Order of A^T = 4 x 3
But A^TB and AB^T is defined.
So, order of B is 3 x 4.

Question 8.
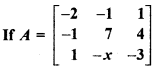, is a symmetric matrix, then determine x.
Solution:
Given,

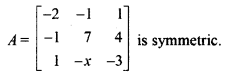
On comparing a_ij = a_ji
a₃₂ = a₂₃ ⇒ -x = 4
∴ x = -4

RBSE Solutions For Class 12 Maths Chapter 3.2 Question 9.
Construct a matrix of order 3 x 3, B = [b_ij], whose elements are b_ij= (i) (j).
Solution:
B₁₁ = 1 x 1 = 1
B₁₂ = 1 x 2 = 2
B₁₃ = 1 x 3 = 3

B₂₁ = 2 x 1 = 2
B₂₂ = 2 x 2 = 4
B₂₃ = 2 x 3 = 6

B₃₁ = 3 x 1 = 3
B₃₂ = 3 x 2 = 6
B₃₃ = 3 x 3 = 9

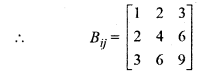
Miscellaneous Ex Ch 3 Class 12 Maths Question 10.

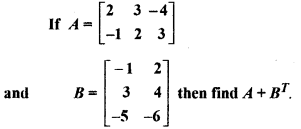
Solution:

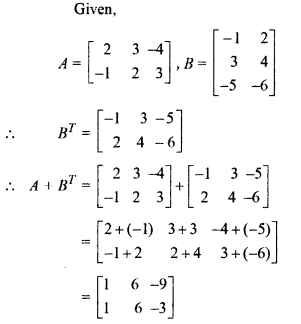
Miscellaneous Exercise On Chapter 3 Class 12 Question 11.
Express matrix A as the sum of symmetric and skew-symmetric matrices, where
.
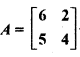Solution:
Given,

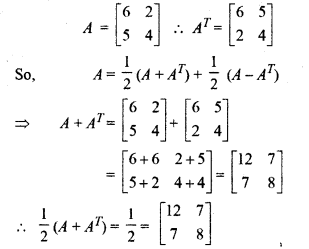
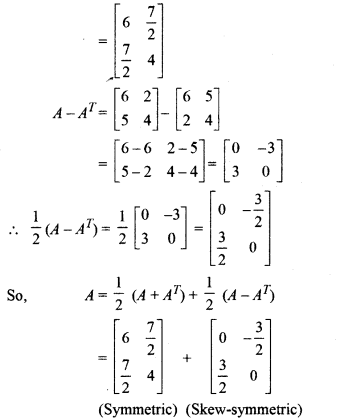
Class 12 Maths RBSE Solutions Question 12.
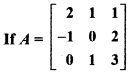then prove that :
(i) (A^T)^T = A
(ii) A + A^T is a symmetric matrix.
(iii) A – A^T is a skew-symmetric matrix.
(iv) AA^T and A^TA are symmetric matrix.
Solution:
(i) (A^T)^T = A

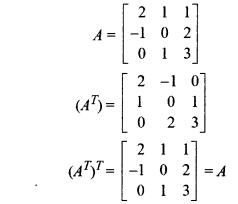
(ii) A + A^T is symmetric


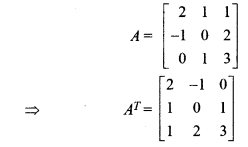
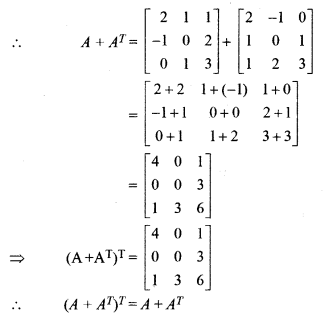
So, A + A^T is symmetric matrix. Hence Proved.

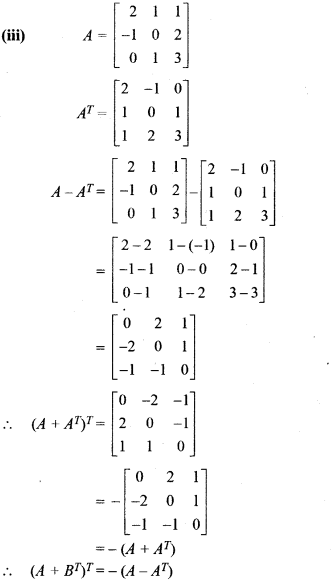
So, A – A^T is skew symmetric matrix. Proved.

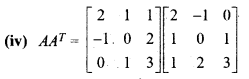
Here,
a₂₁ = a₁₂ = 0
a₃₁ = a₁₃ = 0
a₂₃ = a₃₂ = 6
So, AA^T is symmetric matrix.

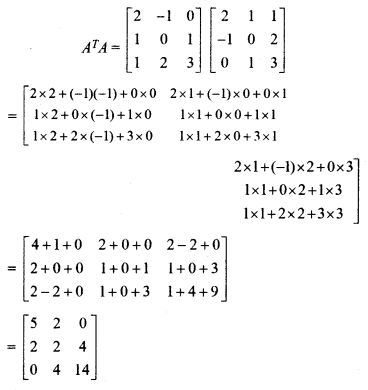
Here,
a₁₂ = a₂₁ = 0
a₁₃ = a₃₁ = 0
a₃₂ = a₂₃ = 4
So, A^TA is symmetric matrix.

Chapter 3 Class 12 Maths Miscellaneous Question 13.
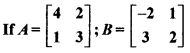, and 3A – 2B + C is a null matrix, then determine matrix ‘C’.
Solution:

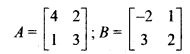
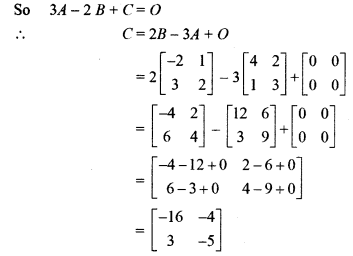
Ex 3 Miscellaneous Class 12 Question 14.
Construct a matrix B = [b_ij] of the order 2 x 3, whose elements are b_ij = (i +2j)²/2
Solution:
Given, B = [b_ij] whose elements are

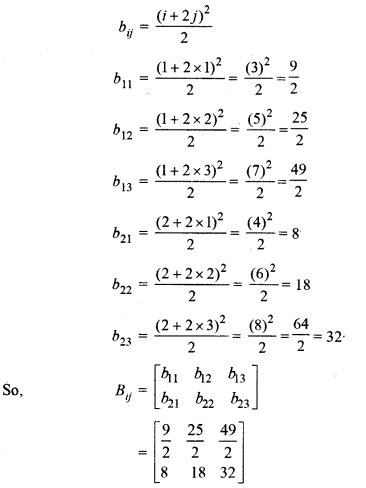
RBSE Solutions For Class 12 Maths Question 15.
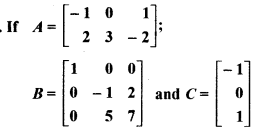, then find the element of 1^st row of ABC.
Solution:

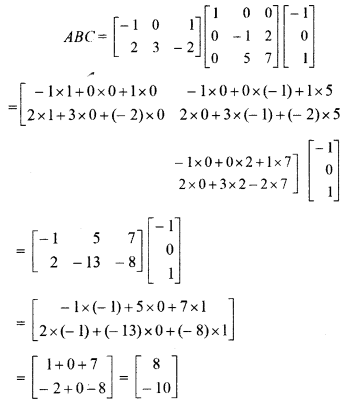
So, element of 1^st row is 8.

Class 12 Maths Ch 3 Miscellaneous Solutions Question 16.
, then find AA^T.
Solution:
Given,

Miscellaneous Chapter 3 Class 12 Question 17.
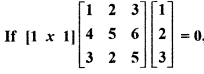, then find x.
Solution:

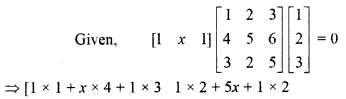
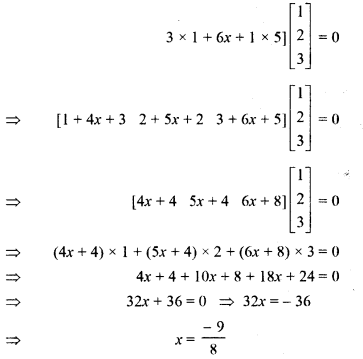
Matrices Class 11 Solutions Question 18.
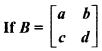, then prove

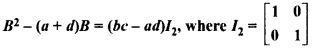
Solution:
Given,

= (bc – ad)I₂ = R.H.S.
Hence Proved.

RBSE Solution Class 12 Maths Question 19.
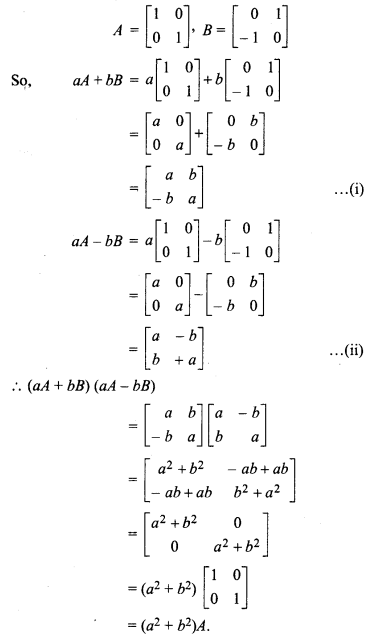
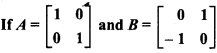, then find the matrix form of the following (aA + bB) (aA – bB).
Solution:
Givn,

RBSE Class 10 Maths Chapter 3 Miscellaneous Question 20.
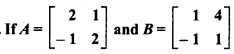, then prove that (A – B)² ≠ A² – 2AB + B².
Solution:
Given,



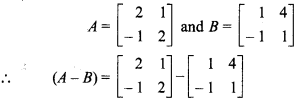
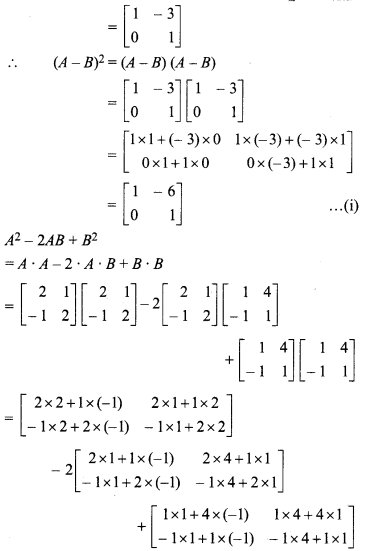
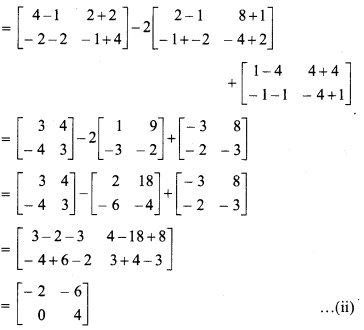
From (i) and (ii),
(A – B)² + A² – 2AB + B²
Hence Proved.

Class 12 Maths Ch 3 Miscellaneous Question 21.
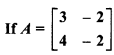, then find k, where A² = kA – 2IA₂ .
Solution:
Given,

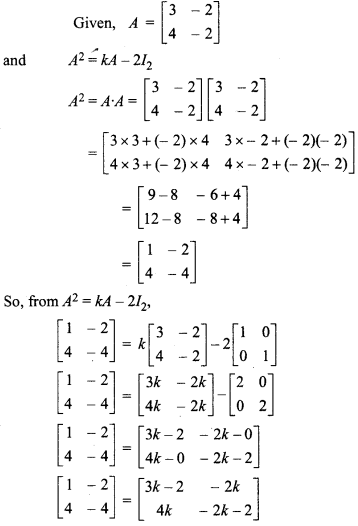
On comparing corresponding element
From 3k – 2 = 1
3k = 3 ⇒ k = \(\frac { 3 }{ 3 }\) ⇒ k = 1.

Matrices Class 12 Miscellaneous Exercise Solutions Question 22.
i = √-1 then prove that :
(1) A² = B² = C² = -I₂
(ii) AB = – BA = -C
Solution:

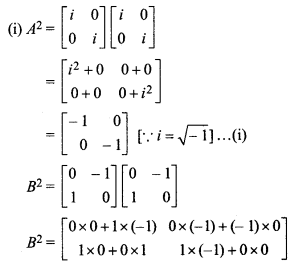
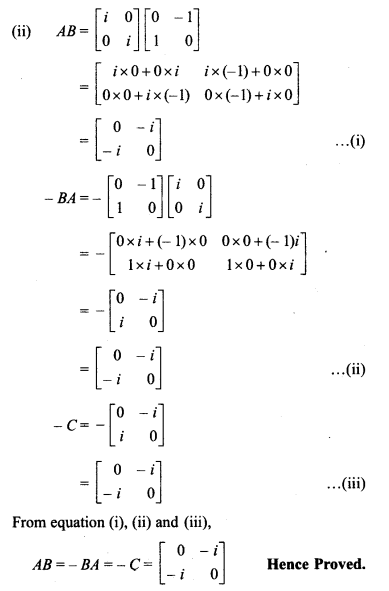
Miscellaneous Exercise On Chapter 3 Question 23.
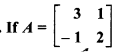and f(A) = A² – 5A + 7I then find f(A).
Solution:

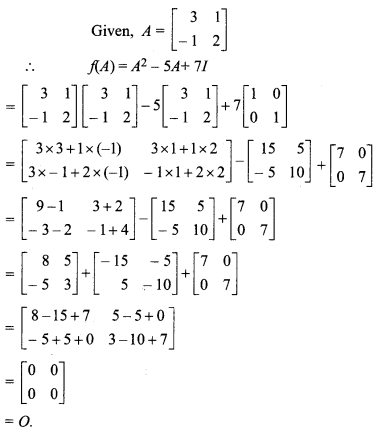
Miscellaneous Exercise Matrices Class 12 Question 24.
Prove that

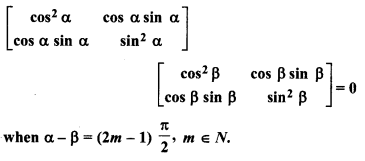
Solution:

RBSE Solutions for Class 12 Maths