RBSE Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.1

Rajasthan Board RBSE Class 12 Maths Chapter 4 Determinants Ex 4.1

Question 1.
For which value of k, det
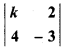will be zero ?
Solution:

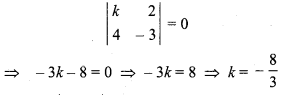
Question 2.
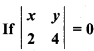, find x : y.
Solution:

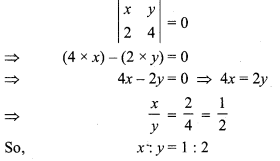
Question 3.
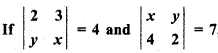, then find the value of x and y.
Solution :

Question 4.
Find x, if

Solution :

⇒ (x – 1) (x – 3) – x(x – 2) = 0
⇒ x² – 3x – x + 3 – x² + 2x = 0
⇒ -2x + 3 = 0
⇒ – 2x = -3
So, x = 3/2

Question 5.
Write minors and co-factors of following determinants corresponding to first column, also find the value of determinants:

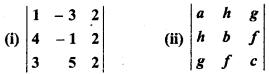
Solution:

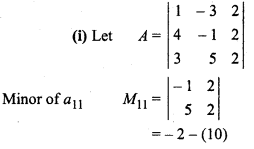
= – 2 – 10 = -12
Cofactor of a
F₁₁ = (- 1)² M₁₁
= 1 x (- 12) = -12
Minor of a²¹

= -6 – 10 = -16
Cofactor of a₂₁
F₂₁ = (- 1)³ M₂₁
= -1 x (-16) = 16
Minor of a₃₁

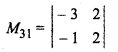
= – 6 – (- 2)
= – 6 + 2 = -4
Cofactor of a₃₁
F₃₁ = (- 1))⁴M₃₁
= 1 x (-4) = -4
So, Determinant M = a₁₁F₁₁ + a₂₁ F₂₁ + a₃₁ F₃₁
= 1 .(- 12) +4·(16) + 3.(-4)
= – 12 + 64 – 12 = 40
So, M₁₁ = -12, M₂₁ = – 16, M₃₁ =-4
F₁₁ = – 12, F₂₁ = 16, F₃₁ = -4
|A| = 40

(ii)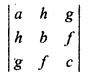
Solution:
Minor of a₁₁

= a . (bc – f²) + h. (fg – hc) + g. (hf – bg)
= abc – af² +fgh – h²c + fgh – bg²
= abc + 2fgh – af² – bg² – ch²
So M₁₁ = bc – f², M₂₁= hc – fg, M₃₁ = hf – bg
F₁₁ = bc – f², F₂₁ = fg – hc, F₃₁ = hf – bg
|A| = abc + 2fgh – af² – bg² – hc²

Question 6.
Find the value of determinant

Solution:

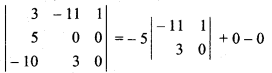
= -5 (0 – 3)
= -5 x (-3) = 15

Question 7.
Prove that :

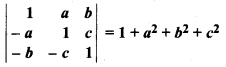
Solution:

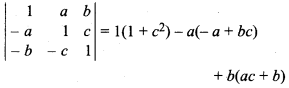
= 1 + c² + a² – abc + abc + b²
= 1 + a² + b² + c² = R.H.S. Proved.

RBSE Solutions for Class 12 Maths