RBSE Solutions for Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

Rajasthan Board RBSE Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

RBSE Solutions For Class 12 Maths Chapter 4 Miscellaneous Question 1.
Value of determinant
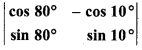is:
(a) 0
(b) 1
(c) -1
(d) none of these
Solution:

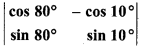
= cos 80° sin 10° – (- cos 109) sin 80°
= cos 80° sin 10° + cos 10° sin 80°
= sin (10° + 80°)
= sin 90° = 1
So, option (b) is correct.

RBSE Class 12 Maths Chapter 4 Miscellaneous Question 2.
Co-factors of first column of determinant

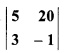
(a) -1, 3
(b) -1,- 3
(c)- 1, 20
(d) – 1,- 20
Solution:

Co-factor of a₁₁
F₁₁ = (- 1)² M₁₁
= 1 x (- 1) = – 1
Co-factor of a₁₂
F₂₁ = (-1)¹¹ M₂₁
= (- 1) × 20 = – 20
So, option (d) is correct.

RBSE Solutions For Class 12 Maths Chapter 4 Question 3.
If 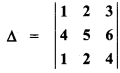, then the value of will be :
(a) – 2∆
(b) 8∆
(c) -8∆
(d) -6∆
Solution:

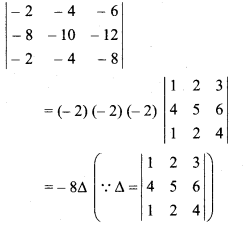
So, option (c) is correct.

Ch 4 Miscellaneous Class 12 Maths Question 4.
Which of the following determinant is identical to determinant
:

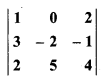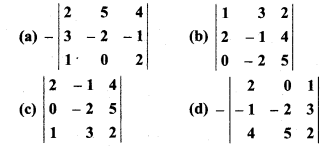
Solution:


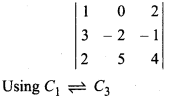
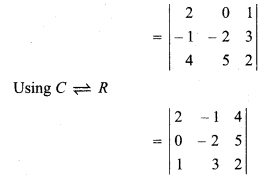
So, option (c) is correct.

RBSE Solution Class 12 Maths Question 5.
Value of

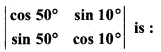
(a) 0
(b) 1
(c) 1/2
(d) – 1/2
Solution:

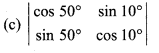
= cos 50° cos 10° – sin 50° sin 10°
= cos (50° + 10°)
= cos 60° = \(\frac { 1 }{ 2 }\)
So, option (c) is correct.

Class 12th Maths RBSE Solution Question 6.
Value of

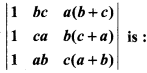
(a) ab + bc + ca
(b) 0
(c) 1
(d) abc
Solution:

RBSE Class 10 Maths Chapter 4 Miscellaneous Solutions Question 7.
If ω is a cube root of unity, then value of

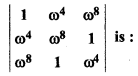
(a) ω²
(b) ω
(c) 1
(d) o
11 04 081
Solution:

RBSE Solution Class 12th Maths Question 8.
If 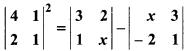, then x will be:
(a) 6
(b) 7
(c) 8
(d) 0
Solution:

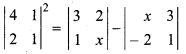
⇒ (4 – 2)² = (3x – 2) – (x + 6)
⇒ (2)² = 3x – 2 – x – 6
⇒ 4 = 2x – 8
⇒ 4 + 8 = 2x
x = 6
So, option (a) is correct.

RBSE Solution Maths Class 12 Question 9.
If and F₁₁, F₁₂, F₁₃, …, are the corresponding cofactors of a₁₁, a₁₂, a₁₃, …, then which of the following is true :
(a) a₁₂F₁₂+ a₂₂F₂₂ + a₃₂F₃₂ = 0
(b) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ ≠ ∆
(c) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = ∆
(d) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = – ∆.
Solution:
a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = ∆
So, option (c) is correct.

RBSE Solution Class 12th Math Question 10.
Value of determinant

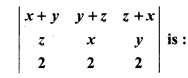
(a) x + y + z
(b) 2(x + y + z)
(c) 1
(d) 0
Solution:

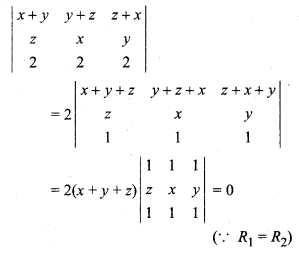
So, option (d) is correct.

RBSE Solution Class 12 Math Question 11.
Solve the following equation :

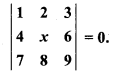
Solution:

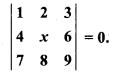
⇒ 1(9x – 48) – 2(36 – 42) + 3(32 – 7x) = 0
⇒ 9x – 48 + 12 + 96 – 21x =0
⇒ – 12x + 60 = 0
⇒ – 12x = -60
⇒ x = \(\frac { 60 }{ 12 }\) = -5
So, x = 5.

RBSE Solutions Maths Class 12 Question 12.
Find the value of determinant :

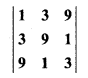
Solution:
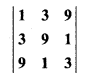= 1(27 – 1) – 3(9 – 9) + 9(3 – 81)
= 26 – 0 – 702
= -676.

Class 12 RBSE Solutions Maths Question 13.
Find the value of determinant

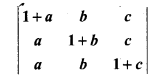
Solution:

Miscellaneous Exercise 4 Class 12 Question 14.
Prove that

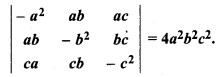
Solution:

= a²b²c² [- 1(1 – 1) – 1(-1 – 1) + 1(1 + 1)]
= a²b²c² (0 + 2 + 2)
= 4a²b²c² = R.H.S. Hence Proved.

RBSE Solution For Class 12 Maths Question 15.
Prove that x = 2 is a root of following equation. Also find its remaining roots :

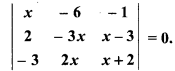
Solution:

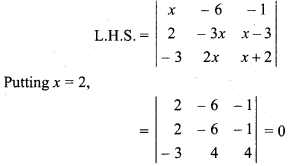
∵ R₁ = R₂
∴ Determinant will be zero.
∴ Root of equation is 2.

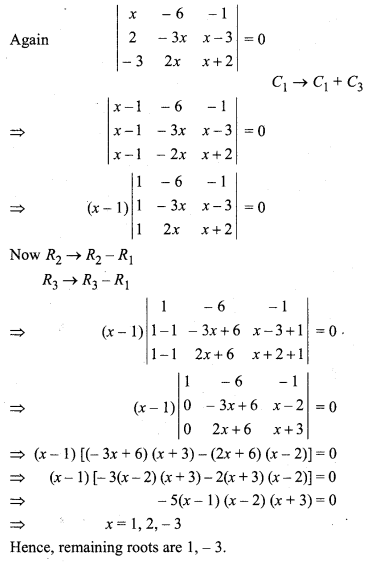
RBSE Solutions For Class 12 Maths Chapter 5 Miscellaneous Question 16.
Prove that:

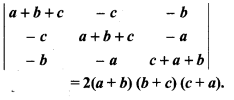
Solution:

RBSE Solutions Class 12th Maths Question 17.
Prove that
.
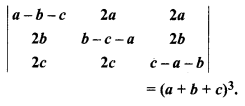Solution:


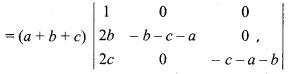
= (a + b + c)[(- b – c – a) (- c – a – b) – 0]
= (a + b + c)(b + c + a)(c + a + b)
= (a + b + c)3 = R.H.S.
Proved.

Class 12 Maths Chapter 4 Miscellaneous Solution Question 18.
Prove that :

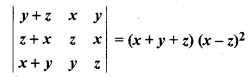
Solution:

Miscellaneous Exercise Chapter 4 Class 12 Question 19.
Prove that:

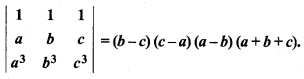
Solution:


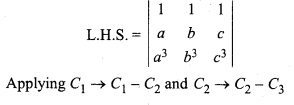
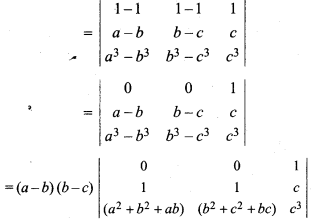
= (a – b) (b – c) [(b² + c² + bc) – (a² + b² + ab)]
= (a – b) (b – c) (b² + c² + bc – a² – b² – ab)
= (a – b)(b – c) [bc + c² – a² – ab]
= (a – b)(b – c) [bc – ab + c² – a² ]
= (a – b) (b – c) [b(c – a) + (c² – a)]
= (a – b)(b – c)(c – a)(b + c + a)
= R.H.S. Proved.

Miscellaneous Exercise On Chapter 4 Class 12 Question 20.
Prove that:

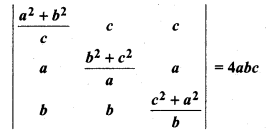
Solution:

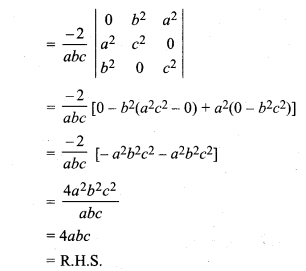
Maths RBSE Solutions Class 12 Question 21.
If a + b + c = 0, then solve:

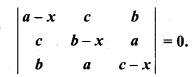
Solution:

⇒ (-x) [(c – a) (a – c + x) – (b – c + x) (b – x – a)] = 0
⇒ (-x) [(ac – c² + cx – a² + ac – ax)
⇒ (b² – bx – ab – bc + cx + ac – xb – x² – ax)] = 0
= (-x) [x² – (a² + b² – ab – bc – bc – ca)]= 0
If – x = 0, then x = 0
Now, if x² = (a² + b² + c² + bc – ab – ca) = 0 .

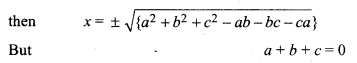
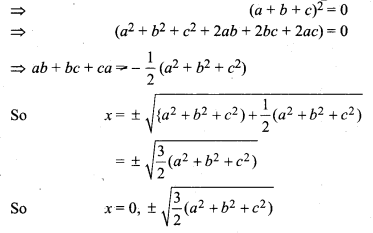
Class 12 Maths Ch 4 Miscellaneous Question 22.
Prove that

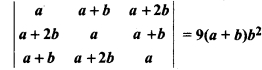
Solution:

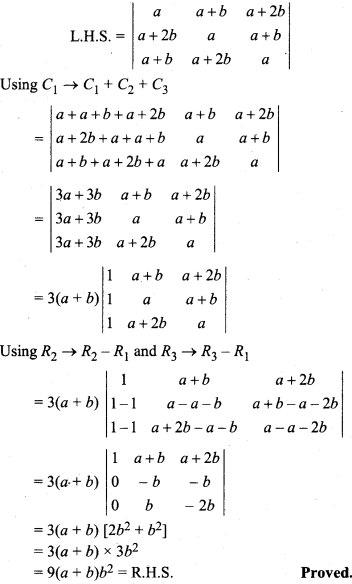
Chapter 4 Miscellaneous Class 12 Question 23.
If p + q + r = 0, then prove that

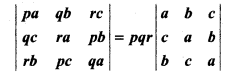
Solution:

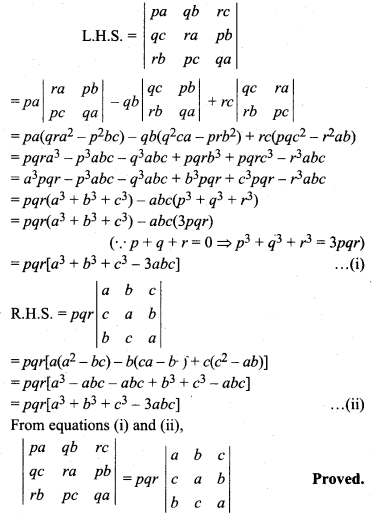
Miscellaneous Chapter 4 Class 12 Question 24.
Prove that

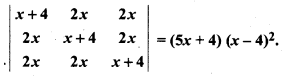
Solution:

RBSE Solutions for Class 12 Maths