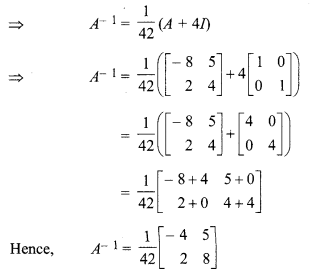RBSE Solutions for Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Ex 5.1

Rajasthan Board RBSE Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Ex 5.1

RBSE Solutions For Class 12 Maths Chapter 5 Question 1.
For which value of x, matrix
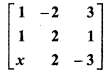is singular ?
Solution:

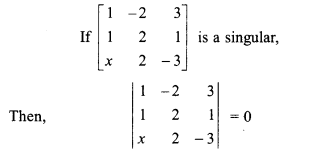
⇒ 1 (- 6 – 2) + 2 (-3 – x) + 3(2 – 2x) = 0
⇒ -8 – 6 – 2x + 6 – 6x = 0
⇒ -8 = 8
⇒ x = \(\frac { 8 }{ -8 }\) = -1
Hence, x = -1

RBSE Solutions For Class 12 Maths Chapter 5.1 Question 2.
If matrix 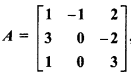, then find adj.A, Also prove that, A(adj.A) = |A| I₃ = (adj.A)A.
Solution:

Matrix made from adjoint of matrix A,

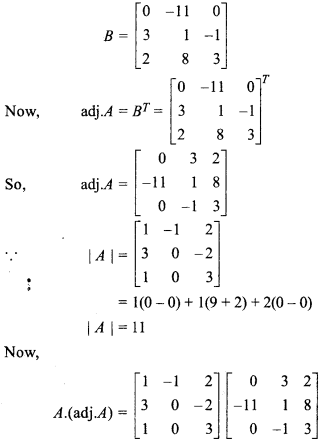
RBSE Solutions For Class 12 Maths Chapter 5 Miscellaneous Question 3.
Find the inverse matrix of the following matrix:

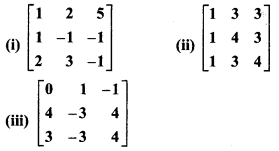
Solution:
(i) Let

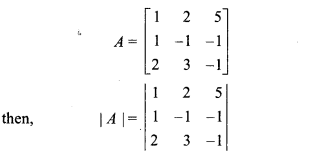
= 1(1 + 3) – 2(-1 + 2) + 5(3 + 2)
= 4 – 2 + 25
|A| = 27 ≠ 0
So. A^-1 exists.
Cofactors of matrix A,

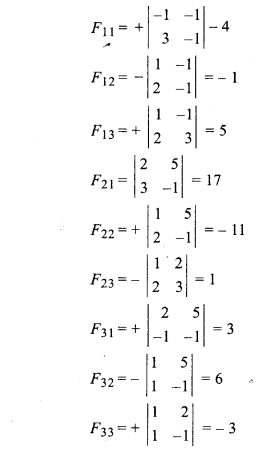
Matrix made from adjoint of matrix A,

Cofactors of matrix A,

Matrix made from adjoint of matrix A,

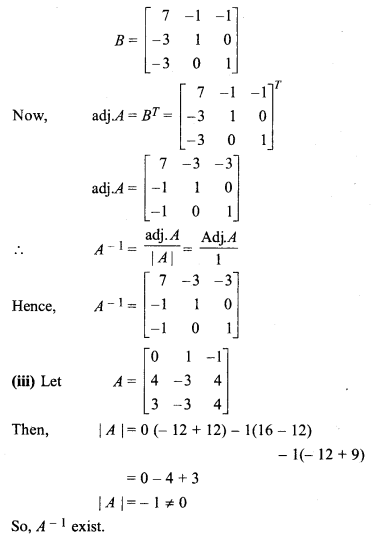
Cofactors of matrix A.


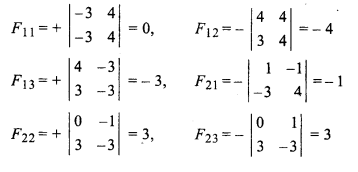
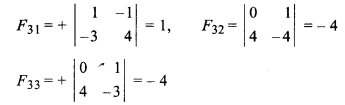
Matrix made from adjoint of matrix A,

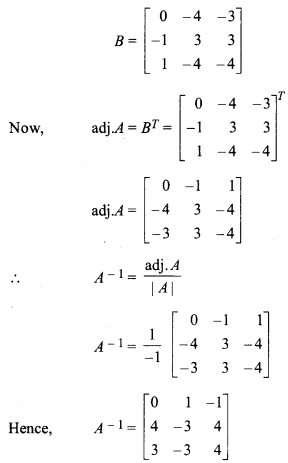
Ex 5.1 Class 12 Question 4.
If matrix

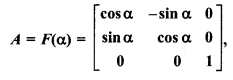
then find A^-1 and prove that:
(i) A^-1A= I3
(ii) A^-1 = F(-α)
(iii) A(adj.A) = |A|I = (adj A).A
Solution:

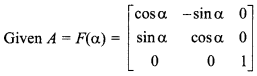
Then, |A| = cos α (cos α – 0) + sin α (sin α – 0) + 0(0 – 0)
= cos² α + sin² α
|A|= 1 ≠ 0 So,
A^-1 exists.
Cofactors of matrix A,

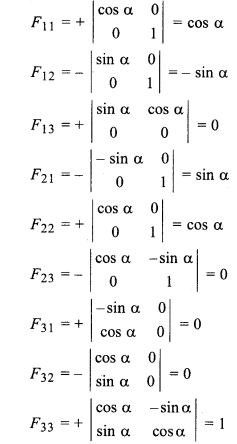
Matrix made from adjoint of matrix A




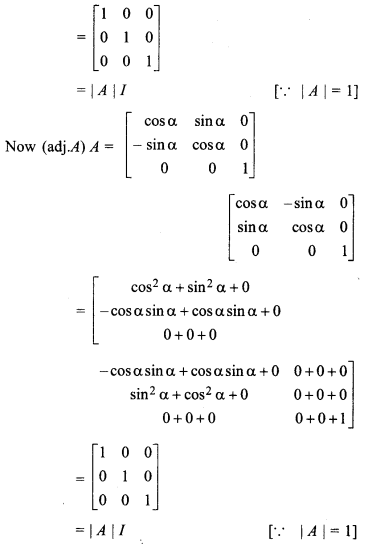
So, A(adj.A) = |A|I = (adj.A) A Hence Proved.

Class 12 Math Chapter 5.1 Solution Question 5.
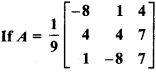, then prove that : A^-1 = A^T.
Solution:
Let

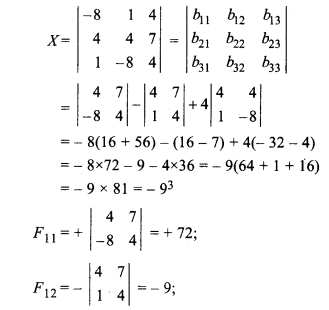
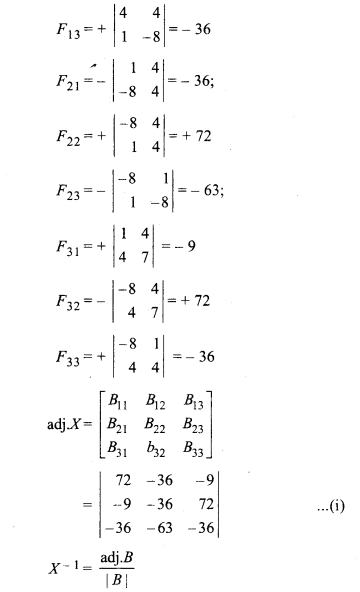
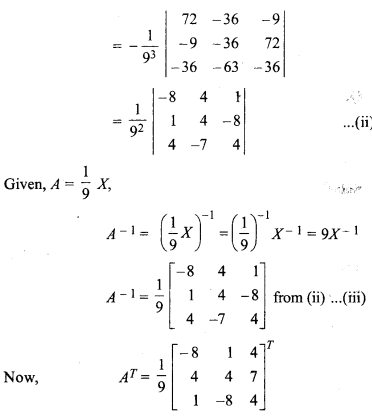
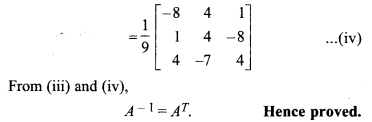
RBSE Solutions For Class 12 Maths Chapter 5.1 Question 6.
If matrix 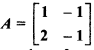, then prove that A^-1 = A³.
Solution:
Given,

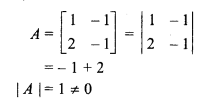
So, A^-1 exists.
On finding adjoint of matrix A,
a₁₁ = – 1, a₁₂ = – 2, a₂₁ = 1, a₂₂ = 1
Matrix formed by adjoint of A,

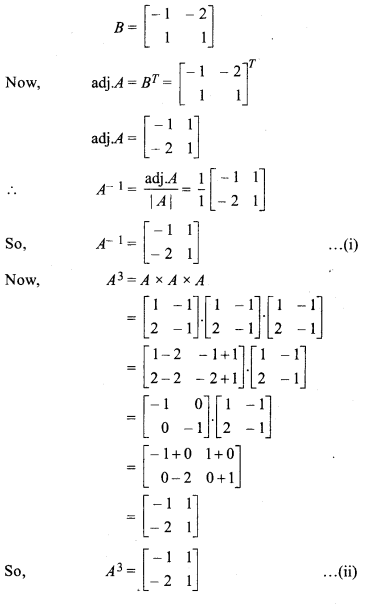
From (i) and (ii),
A^-1 = A³
Hence proved.

Exercise 5.1 Class 12 Question 7.

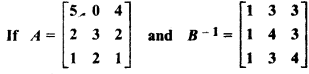
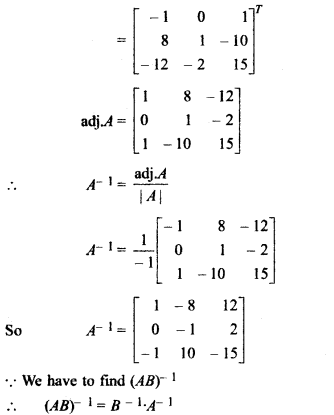
then find (AB)^-1.
Solution:
Given

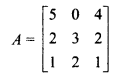
Then, |A| = 5(3 – 4) – 0(2 – 2) + 4(4 – 3)
= – 5 – 0 + 4
|A| = -1 ≠ 0
So, A^-1 exists.
On finding adjoint of matrix A,

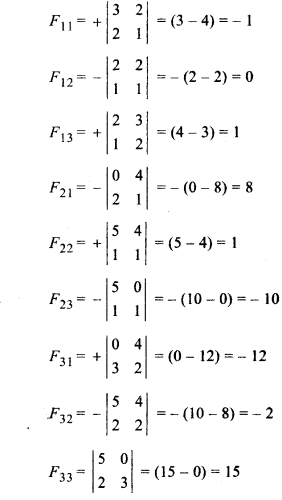
Matrix formed by adjoint of A

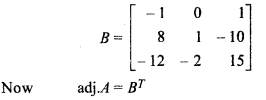
RBSE Solutions For Class 12 Maths Chapter 5 Question 8.
If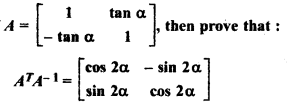
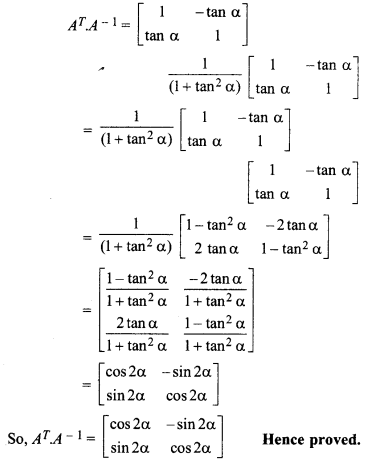
Solution:
Given

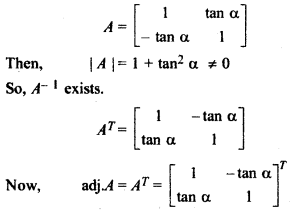
Matrix 5.1 Question 9.
Show prove that matrix 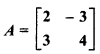satisfies equation A² – 6A + 17I = O. Thus find A^-1.
Solution:
Given

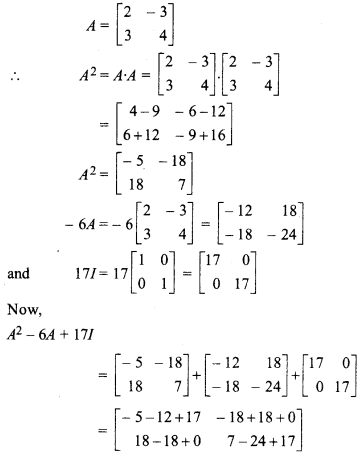
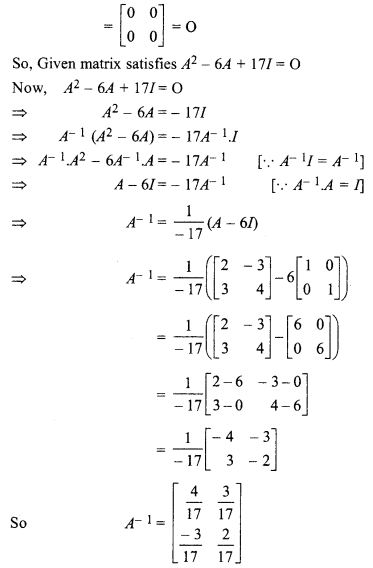
Maths Chapter 5 Class 12 Question 10.
If matrix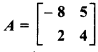
, then show that A² + 4A – 42I = O. Hence A².
Solution:
Given


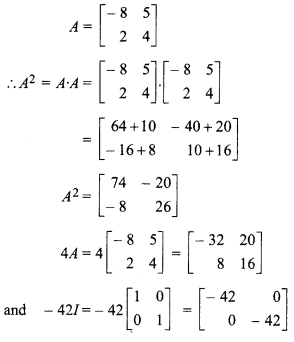
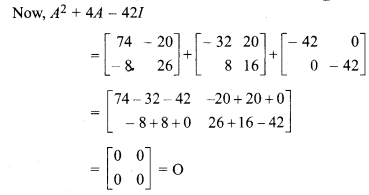
So, given matrix satisfies A² + 4A – 42I = O
Now A² + 4A – 42I = O
⇒ A² + 4A = 42I
⇒ A^-1 (A² + 4A) = 42A^-1.I
⇒ A^-1.A² + 4A^-1.A = 42A^-1.I
⇒ A + 4I = 42A^-1
(∵ A^-1.A = I and A^-1.I = A^-1)

RBSE Solutions for Class 12 Maths