RBSE Solutions for Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Miscellaneous Exercise

Rajasthan Board RBSE Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Miscellaneous Exercise

RBSE Solutions For Class 12 Maths Chapter 5 Miscellaneous Question 1.
If A = 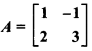, then find A^-1.
Solution:

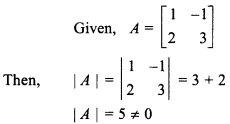
So, A^-1 exists.
On finding adjoint of A,
F₁₁ = 3, F₁₂ = – 2, F₂₁ = 1, F₂₂ = 1
Matrix formed by adjoint A,

RBSE Solutions For Class 12 Maths Chapter 5 Question 2.
If 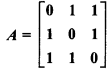, then find A^-1.
Solution:

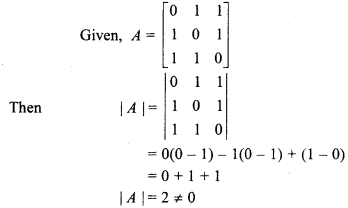
So, A^-1exists.
On finding adjoint of A,

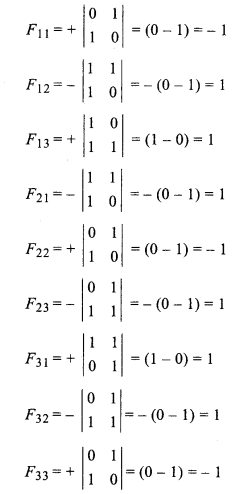
Matrix formed by adjoint of A,

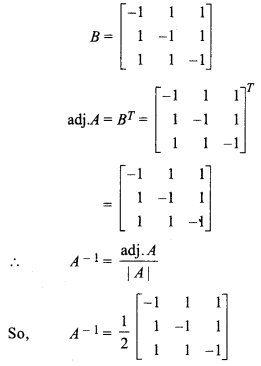
12 Maths RBSE Solution Question 3.
If matrix 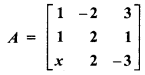is a singular matrix, then find x.
Solution:

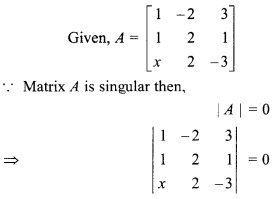
⇒ (- 6 – 2) + 2(- 3 – x) + 3(2 – 2x) = 0
⇒ – 8 – 6 – 2x + 6 – 6x = 0
⇒ – 8 – 8x = 0
⇒ x = \(\frac { 8 }{ -8 }\)
⇒ x = -1
⇒ Hence, x = -1

Miscellaneous Chapter 5 Class 12 Question 4.
Use Cramer’s rule to solve the following system of equations :

(i) 2x – y = 17
3x + 5y = 6

(ii) 3x + ay = 4
2x + ay= 2, a ≠ 0

(iii) x + 2y + 37 = 6
2x + 4y + z = 7
3x + 2y + 9z = 14
Solution:
(i) Given,
2x – y = 17
3x + 5y = 6

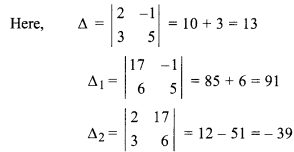
∵ ∆ ≠ 0, ∆₁ ≠ 0 and ∆₂ ≠ 0
∴ Solution will be unique.
By using Cramer’s rule

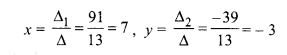
Hence, solution is x = 7, y = -3

(ii) Given,
3x + ay = 4
2a + ay = 2,
a ≠ 0

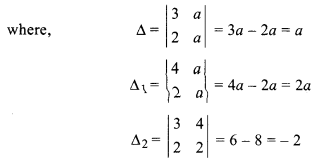
∵ ∆ ≠ 0, ∆₁ ≠ 0 and ∆₂ ≠ 0
∴ Solution will be unique.
Using Cramer’s rule

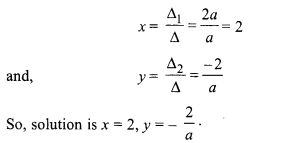
(iii) Given,
x + 2y + 2x = 6
2x + 4y + z = 7
3x + 2y + 92 = 14

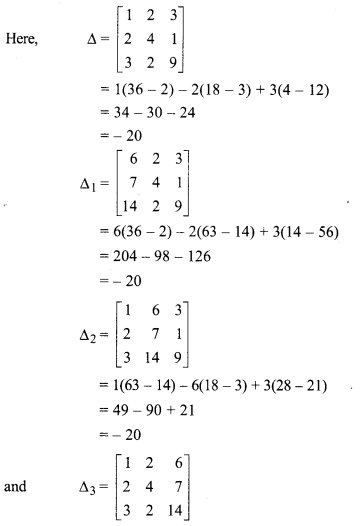
= 1(56 – 14) – 2(28 – 21) + 6(4 – 12)
= 42 – 12 – 48
= -20
∵ ∆ ≠ 0, ∆₁ ≠ 0 , ∆₂ ≠ 0 and ∆₃ ≠ 0
∴ Solution will be unique.
Using Cramer’s rule,

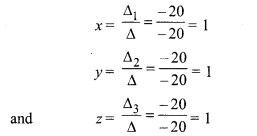
Hence, solution is x = 1, y = 1, z = 1.

RBSEsolution.Com Class 12 Maths Question 5.
Use Cramer’s rule and prove that following system of equations are inconsistent :
(i) 2x – y = 5
4x – 2y = 7

(ii) x + y + z = 1
x + 2y + 37 = 2
3x + 4y + 5y = 3
Solution:
(i) Given,
2x – y = 5
4x – 2y = 7

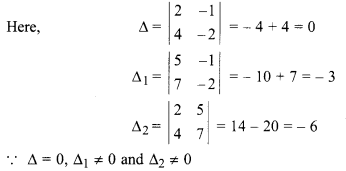
Hence, system of equations is inconsistent.

(ii) Given,
x + y + z = 1
x + 2y + 3z = 2
3x + 4y + 3z = 3

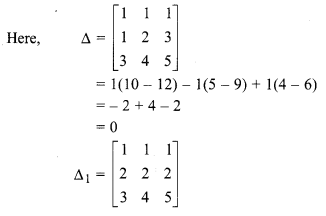
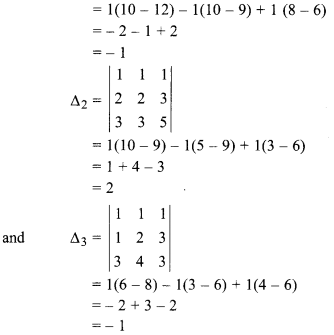
∵ ∆ ≠ 0, ∆₁ ≠ 0 , ∆₂ ≠ 0 and ∆₃ ≠ 0
Hence, system of equations is inconsistent.

12th Maths RBSE Solution Question 6.
Find a matrix A of order 2, where

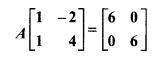
Solution:

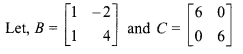
Then,
AB = C
ABB^-1 = CB^-1
AI = CB^-1 [∵ BB^-1 = I]
A = CB^-1 …….(i)
[∵ AI = A]

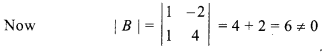
So, B^-1 exists.
On finding adjoint of B,
F₁₁ = 4, F₁₂ = -1, F₂₁ = 2, F₂₂ = 1
Matrix formed by adjoint of B,

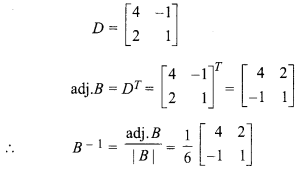
From equation (i),
A = C.B^-1

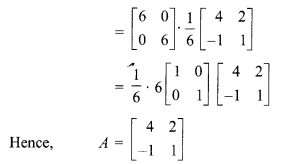
Chapter 5 Class 12 Miscellaneous Question 7.
If 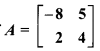then prove that A² + 4A – 42I = 0, also find A^-1.
Solution:

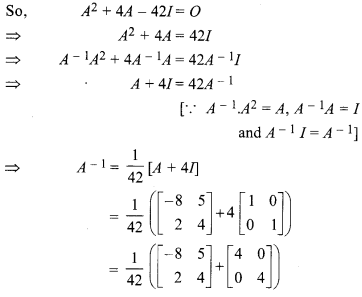
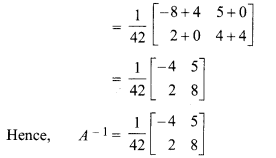
Chapter 5 Miscellaneous Class 12 Question 8.
If 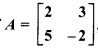then prove that A^-1 = \(\frac { 1 }{ 19 }\) A.
Solution:

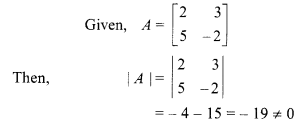
So, A^-1exists.
On finding adjoint of A,
F¹¹ = – 2, F¹² = – 5, F²¹ = – 3, F²² = 2
Matrix formed by adjoint of A,

Class 12 Maths Chapter 5 Miscellaneous Exercise Solutions Question 9.
If 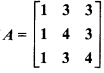, then find A^-1 and show that A^-1.A= I₃.
Solution:

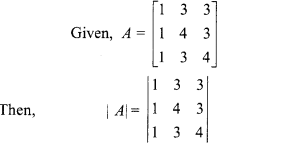
= 1(16 – 9) – 3(4 – 3) + 3(3 – 4)
= 7 – 3 – 3
|A|= 1 ≠ 0
So, A^-1 exists.
On finding adjoint of A,

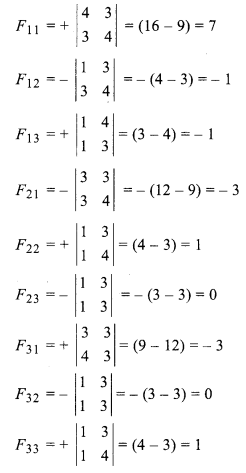
Matrix formed by adjoint of A,

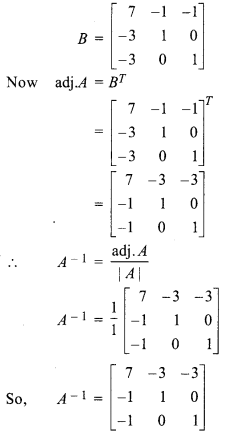
Again to prove that

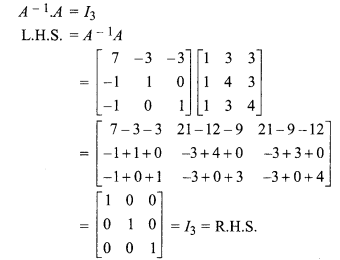
Hence, A^-1A = I₃.

Ch 5 Miscellaneous Class 12 Question 10.
If 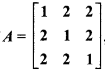, then prove that A² – 4A – 5I = 0, also find A^-1.
Solution:

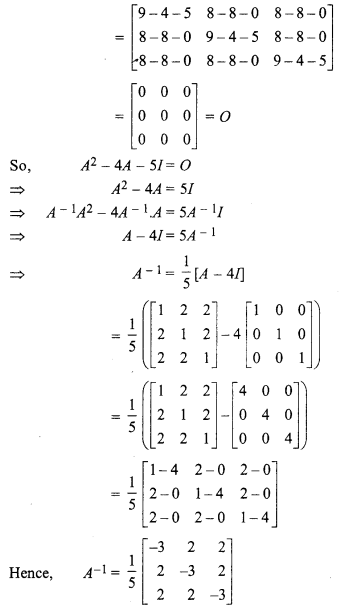
Class 12 Maths Chapter 5 Question 11.
Use matrix method to solve following system of equations :

(i) 5x – 7y = 2
7x – 5y = 3

(ii) 3x + y + z = 3
2x – y – z = 2
– x – y + z = 1

(iii) x + 2y – 2z + 5 = 0
– x + 3y + 4 = 0
– 2y + 7 – 4 = 0
Solution:
(i) Given equations
5x – 7y = 2
7x – 5y = 3
In matrix form AX= B ….(i)…(i)

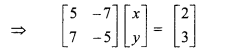
Determinant of matrix A,

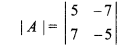
= – 25 + 49 = 24 ≠ 0
So, A^-1 exists.
On finding adjoint of matrix A
F₁₁ = – 5, F₁₂ = – 7, F₂₁ = 7, F₂₂ = 5
Matrix formed by adjoint of A

(ii) Given equations
3x + y + z = 3
2x – y – z = 2
– x – y + z = 1
In matrix form
AX = B ….(i)

= 3(-1 – 1) – 1(2 – 1) + 1(-2 – 1)
= -6 – 1 – 3
= -10 ≠ 0
So, A^-1 exists.
On finding adjoint of A,

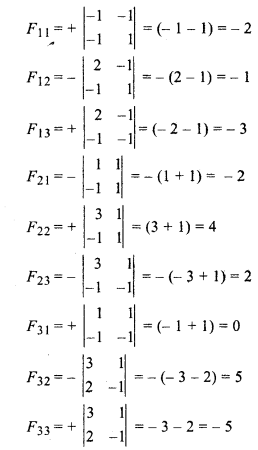
Matrix formed by adjoint of A,

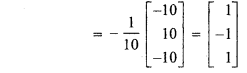
Hence, x = 1, y = -1, z = 1

(iii) Given equations,
x + 2y – 2z + 5 = 0 or x + 2y – 2z = – 5
-x + 3y + 4 = 0 or – x + 3y = – 4
– 2y +z – 4 = 0 or – 2y + z = 4
In matrix form, AX= B ….. (i)

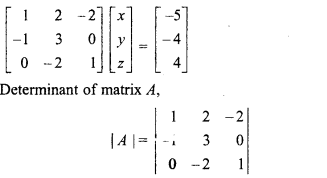
= 1(3 – 0) – 2(-1 – 0) – 2(2 – 0)
= 3 + 2 – 4 = 1 ≠ 0
So, A^-1exists.
On finding adjoint of A,

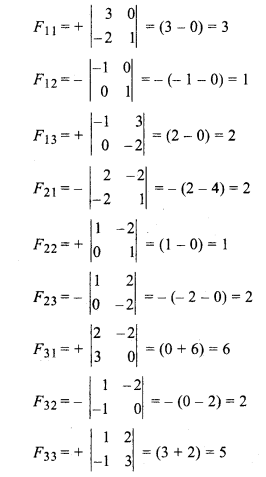
Matrix formed by adjoint of A,

Hence, x = 1, y = – 1, z = 2.

5 Miscellaneous Class 12 Question 12.
Find area of ∆ABC, if vertices are :
(i) A(- 3, 5), B(3, – 6), C(7, 2)
(ii) A(2, 7), B(2, 2), C(10, 8)
Solution:
(i) Vertices of ∆ABC
A = (-3,5), B = (3, -6), C = (7, 2)
Area of ∆ABC

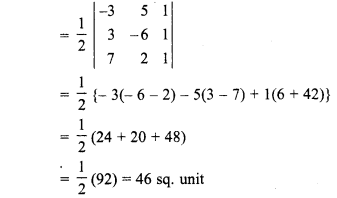
(ii) Vertices of ∆ABC, A = (2, 7), B = (2, 2), C = (10,8)
Area of ∆ABC

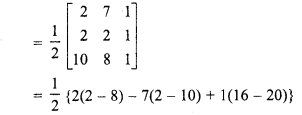
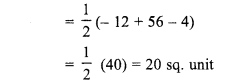
Miscellaneous Exercise On Chapter 5 Class 12 Question 13.
If points (2, – 3), (λ, – 2) and (0, 5) are collinear, then find λ.
Solution:
Given points (2, – 3), (λ, – 2) and (0, 5) are collinear, then

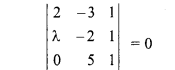
⇒ 2(-2 – 5) + 3(λ – 0).+ 1(5λ – 0) = 0
⇒ – 14 + 3λ + 5λ = 0
⇒ 8λ = 14
⇒ λ = \(\frac { 14 }{ 8 }\) = \(\frac { 7 }{ 4 }\)

Chapter 5 Maths Class 12 Question 14.
Find matrix A, if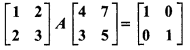
Solution:

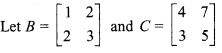
Given, equation BAC = I ……(i)

On finding adjoint of C,
F₁₁ = 5, F₁₂ = – 3, F₂₁ = – 7, F₂₂ = 4
Matrix formed by adjoint of C,

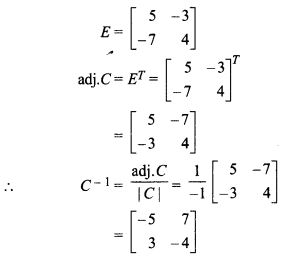
From equation (i)
BAC = I
⇒ B^-1(BAC)C^-1 = B^-1C^-1
⇒ (B^-1B)A(CC^-1) = B^-1C^-1
⇒ IAI = B^-1C^-1
⇒ (IA)I = B^-1C^-1
⇒ AI = B^-1C^-1
⇒ A = B^-1C^-1

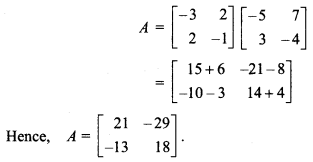
Question 15.
If 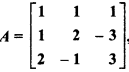, then find A^-1 and solve the following system of equations, using it :
x + y + z = 2,
x + 2y – 37 = 13,
2x – y + 37 = -7.
Solution:
Given

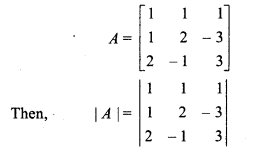
= 1(6 – 3) – 1(3+6) + 1(- 1 – 4)
= 3 – 9 – 5
= -11 ≠ 0
so, A^-1 exists.
On finding adjoint of A,

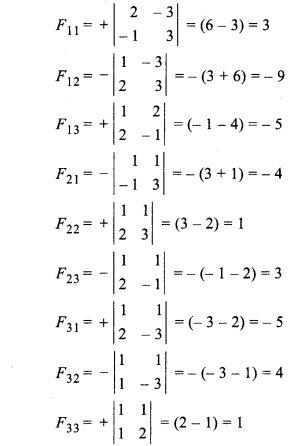
Matrix formed by adjoint of A,

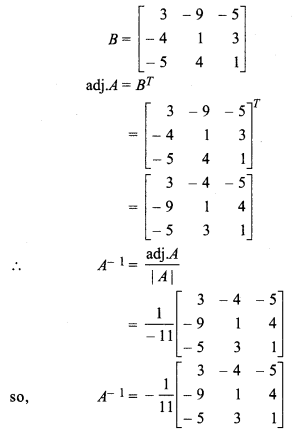
Given equations,
x + y + z = 2
x + 2y – 3z = 13
2x – y + 3z = -7
In matrix form,

Question 16.
If 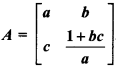, then find A^-1 and show that aA^-1 = (a² + bc + 1)I – aA.
Solution:
Given,

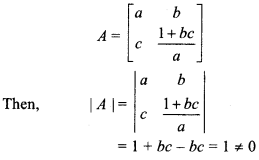
So, A^-1 exists.
On finding adjoint of A,

Question 17.
Using determinant solve the following system of equations:
x + y + z = 1
ax + by + cz = k
a²x + b²y + c²z = k²
Solution:
Given equations,
x + y + z = 1
ax + by + cz = k
a²x + b²y + c²z = k²

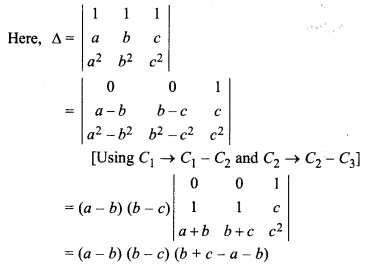
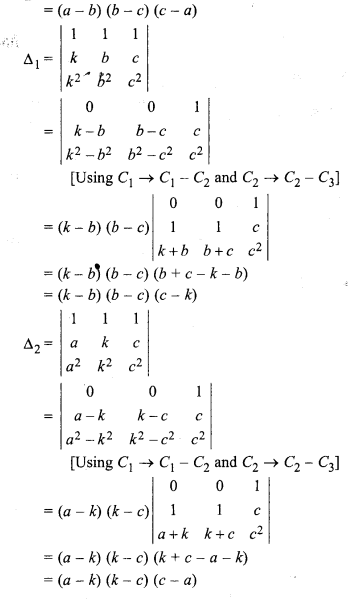
Question 18.
If 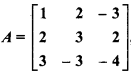, then find A^-1 and solve the following system of equations using it :
x + 2y – 3z = – 4,
2x + 3y + 2z = 2,
3x – 3y – 4z = 11
Solution:

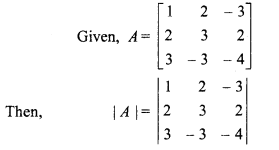
= 1(- 12 + 6) – 26 – 8 – 6) – 3(- 6 – 9)
= -6 + 28 + 45
= 67 ≠ 0
So, A^-1 exists.
On finding adjoint of A,


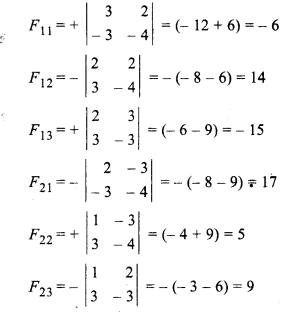
Given equations,
x + 2y – 32 = -4
2x + 3y + 2z = 2
3x – 3y – 4z = 11
In matrix form,

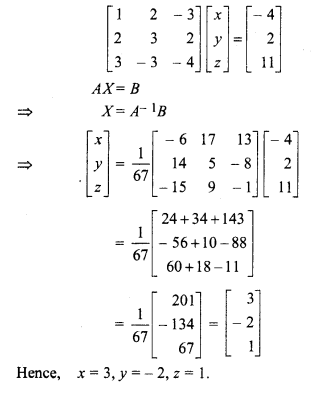
Question 19.
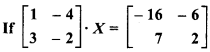, then find the value of X.
Solution:

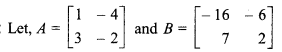
Then, AX = B
X = A^-1B …..(i)
Determinants of matrix A,

So, A^-1 exists.
F₁₁ = – 2, F¹² = – 3, F²¹ = 4, F²² = 1
Matrix formed by adjoint of A,

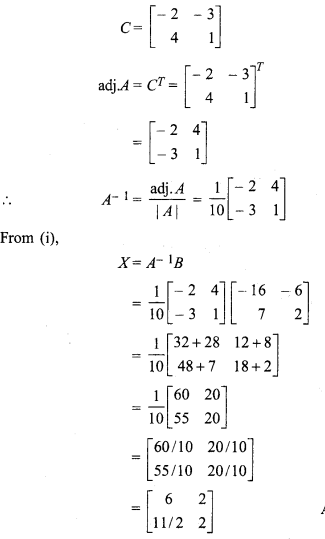
Question 20.
Find the value of a and b, if following system of equations has infinite solutions :
2x + y + az = 4
5x – 2y + z = -2
5x – 5y + z = -2
Solution:
Given equations,
2x + y + az = 4 :
bx – 2y + z = -2
5x – 5y + z = -2
∵ For infinite solution ∆ = 0, ∆₁ = 0, ∆₂ = 0 and ∆_z = 0.

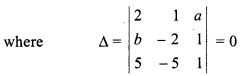
⇒ 2(- 2 + 5) – 1(b – 5) + d(-5b + 10) = 0
⇒ 6 – b + 5 – 5ab + 10a = 0
⇒ 10a – b – 5ab = -11 …(1)

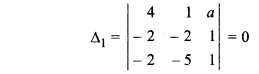
4(-2 + 5) – 1(-2+2) + a(10 – 4) = 0
⇒ 12 + 6a=0
⇒ 16a = -12
a = \(\frac { -12 }{ 6 }\) = -2
From (i),
10a – b – 5ab = -11
⇒ 10(-2) – b – 5(-2)b = -11
⇒ -20 – b + 10b = -11
⇒ 9a = 9
⇒ b = \(\frac { 9 }{ 9 }\)
Hence, a = -2, b = 1.

RBSE Solutions for Class 12 Maths