Rajasthan Board RBSE Class 12 Maths Chapter 7 Differentiation Ex 7.6
Question 1.
Verify the Rolle’s theorem, for the following functions :
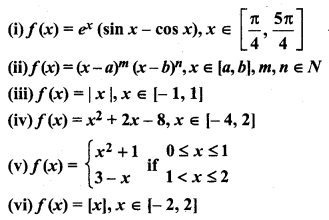
Solution:
(i) Given function
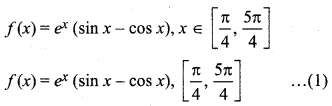
∵ f(x) is polynomial in x.
∴ It is differentiable and continuous every-where.
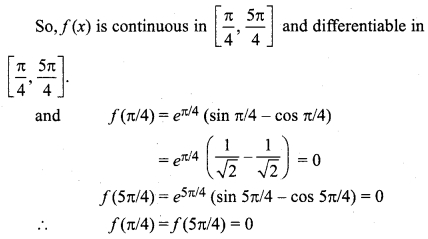
Hence, f(x) satisfies Rolle’s theorem in interval [π/4, 5π/4]
From(1),
f'(x) = ex (cos x + sin x) + (sin x – cos x).ex
f'(x) = ex (cos x + sin x + sin x – cos x)
Similarly,
ec 2 sin c = 0
⇒ 2sinc = 0 ⇒ sin c = 0 ⇒ c = π
c = π ∈ (π/4, 5π/4),f(c) = 0
∴ Hence, Rolle’s theorem satisfied.
(ii) f(x) = (x – a)m (x – b)n, x ∈ [a, b], m, n ∈ N
Here, (x – a)m and (x – b)n both are polynomial. On its multiplication a polynomial of power (m + n) is obtained. A polynomial function is continuous everywhere always.
So, f(x) is continuous in [a, b]. Polynomial function is also differentiable.
∴ f'(x) = m(x- a)m-1 .(x – b)n + n(x – d)m (x – b)n-1
= (x – a)m-1 (x – b)n-1 × [m(x – b) + n(x – a)]
= (x – a)m-1 (x – b)n-1 × [(m + n) x – mb – na]
Here,f'(x) exists.
∴ f(x) is differentiable in interval (a, b).
Again f(a) = (a – a)m (a – b)n = 0
f (b) = (b – a)m (b – b)m-n = 0
∴ f(a) = f(b) = 0
Hence, Rolle’s theorem satisfies,then in interval (a, b) at least any one point is such that f'(c) = 0.

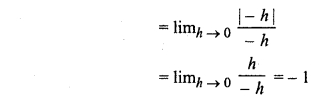
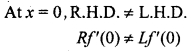
Function is not diffenentiable at x = 0. So, Rolle’s theorem does not satisfied.
(iv) Given function
f(x) = x2 + 2x – 8, x ∈ [- 4, 2]
Here, it is clear that function f(x) is continuous in interval [- 4, 2] and f’ (x) is finite and exist at every point of interval, (- 4, 2), hence given function is differentiable in interval (-4, 2).
∵ f (- 4) = 0 = f (2)
⇒ f (- 4) = f(2)
So, from above f'(x) satisfies all the three conditions of Rolle’s theorem in given interval.

![]()
(vi) Given function
f(x) = [x], x ∈ [- 2, 2]
∵ f(x) is not continuous in [- 2, 2] as greatest integer function is neither continuous nor differentiable.
Hence, Rolle’s theorem does not satisfied.
Question 2.
Prove Rolle’s theorem for following functions :
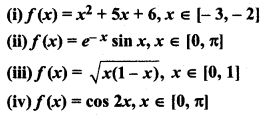
Solution:
(i) Given function
f(x) = x2 + 5x + 6, x ∈ [- 3, – 2]
∵ f(x) = x2 + 5x + 6 is a polynomial function.
Hence, it is continuous in [- 3, – 2],
Now f'(x) = 2x + 5, exists ∀ x ∈ (-3,-2)
∴ f (x) is differentiable in (- 3, – 2)
∵ f (- 3) = 0 = f (- 2)
⇒ f (- 3) = f (- 2)
All the condition of Rolle’s theorem is satisfied, then a point c ∈ (-3,-2) exists in such a way that f'(c) = 0.

All the conditions of Rolle’s theorem satisfied, then a point c in (0,π) exists in such a way that f'(c) = 0.
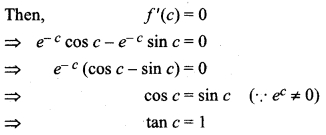

(iii) Given function
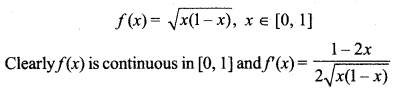
is finite and exist at every point in interval (0, 1).
Hence,f(x) is differentiable in (0, 1).
∵ f(0) = 0 = f(1)
⇒ f (0) = f (1)
So, f (x) satisfies all the conditions of Rolle’s theorem.
Hence, f'(c) = 0

(iv) Given function
f (x) = cos 2x, x ∈ [0, π]
⇒ f (x) = cos 2x is defined in [0,π].
∵ cosine is continuous in its domain.
So, it is continuous in [0, π].
Then, f'(x) = – 2 sin 2x exists,
where x ∈ (0, π)
∴ f (x) is differentiable in (0, π).
Now f(0) = cos 0 = 1
and f(π) = cos 2π = 1
∴ f(0) = f(π) = 1
Thus, all the conditions of Rolle’s theorem, are satisfied then at least one point c such that c ∈ (0, π) and f’ (c) = 0.
f'(c) = 0
∴ f'(c) = – 2 sin 2c = 0
⇒ sin 2c = 0 ⇒ 2c = π
c = π/2 is an element of (0,π)
∴ c = \(\frac { \pi }{ 2 } \) ∈ (0,π)
such that
f'(c) = 0
Thus for c = \(\frac { \pi }{ 2 } \), Rolle’s theorem satisfied.
Question 3.
Verify the Lagrange’s mean value theorem for the following functions :
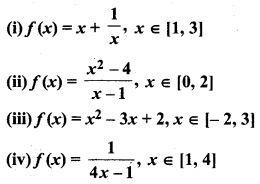
Solution:

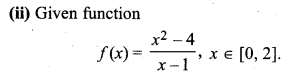
Clearly, f(x) is continuous in interval [0, 2] and f'(x) is finite and exists. So,f(x) is differentiable in (0, 2). Hence f(x) satisfies both conditions of Langrange’s mean value theorem.
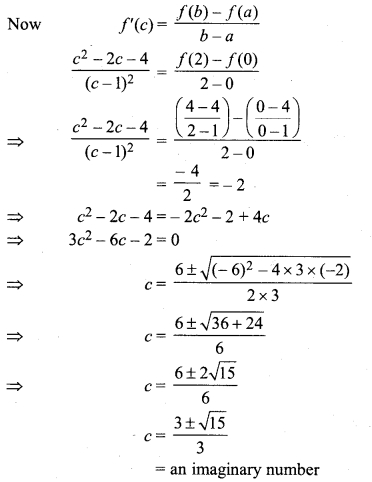
∵ c is an imaginary number.
Hence, Langrange’s mean value theorem does not satisfied.
(iii) Given function
f(x) = x2 – 3x + 2, x ∈ [- 2, 3]
Clearly,f(x) is continuous in interval [-2, 3] and f'(x) is finite and exists in (-2, 3). So, f(x) is differentiable in (- 2, 3). Hence f(x) satisfies both conditions of Langrange’s mean value theorem.
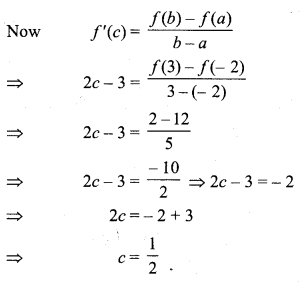

Clearly,f(x) is continuous in [ 1,4] and f'(x) is finite and exist in interval (1,4). Hence,f(x) is differentiable in (1, 4). f(x) satisfies both conditions of Langrange’s mean value theorem.

Thus, Langrange’s mean value theorem satisfied.