RBSE Solutions for Class 12 Maths Chapter 7 Differentiation Miscellaneous Exercise

Rajasthan Board RBSE Class 12 Maths Chapter 7 Differentiation Miscellaneous Exercise

Differentiate given functions from question 1 to 10 w.r.t. x :

RBSE Solutions For Class 12 Maths Chapter 7 Miscellaneous Question 1.
sin^-1 (x\(\sqrt { x }\)), 0 ≤ x ≤ 1.
Solution:
Let y = sin^-1 (x\(\sqrt { x }\))
Diff. w.r.t. x on both sides,

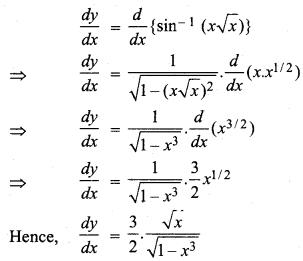
RBSE Class 12 Maths Chapter 7 Miscellaneous Question 2.

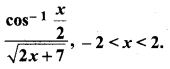
Solution:

Question 3.

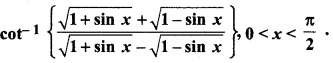
Solution:

RBSE Solutions For Class 12 Maths Chapter 7 Question 4.
x³,e^x,sin x.
Solution:
Let y = x³.e^x.sin x
Diff. w.r.t. x on both sides,

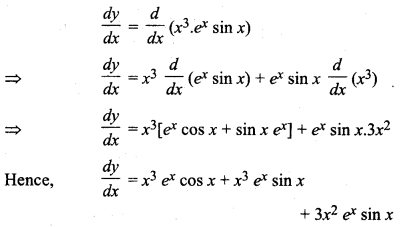
RBSE Solution Class 12 Maths Chapter 7 Question 5.
log (\(\frac { x }{ { a }^{ x } } \))
Solution:

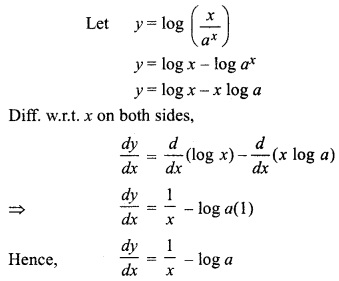
RBSE Solutions For Class 12 Maths Question 6.
(x log x)^{log x,}
Solution:
Let y = (x log x)^{log x}
Taking log of both sides,
log y = log (x log x)^{log x}
⇒ log y = log x.log (x log x)
Diff. w.r.t. x on both sides,

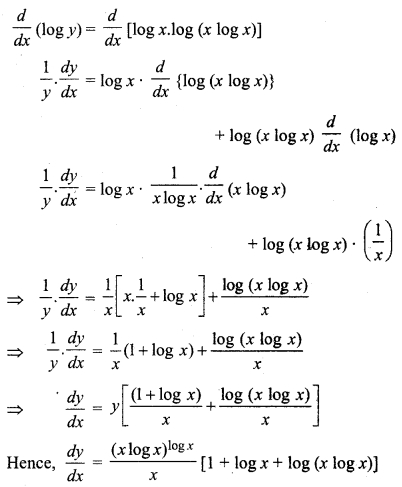
RBSE Solutions For Class 12th Maths Question 7.

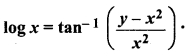
Solution:

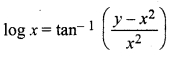
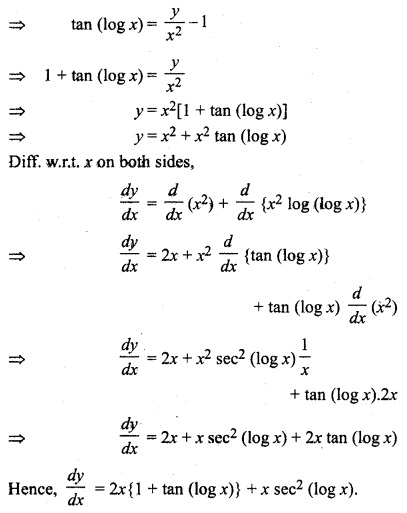
12th Maths RBSE Solution Question 8.
x^x2 – 3 + (x – 3)^x2, x > 3
Solution:

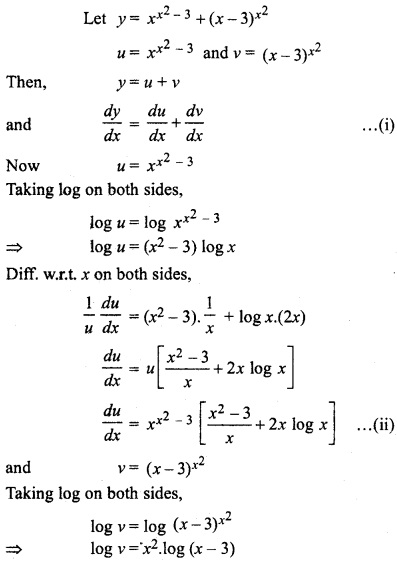
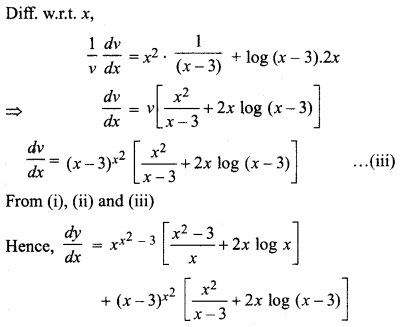
RBSE Solution Class 12th Maths Question 9.
y – 12(1 – cos t),x = 10(t – sin t).
Solution:
Diff. w.r.t. x on both sides,

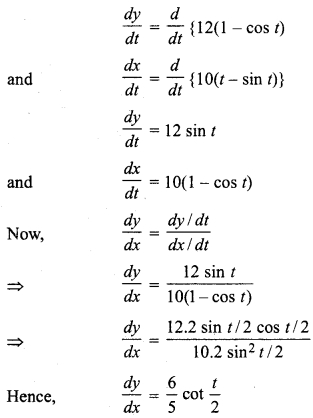
RBSE Solution 12th Math Question 10.
sin^-1 x + sin^-1 \(\sqrt { 1-{ x }^{ 2 } } \)
Solution:

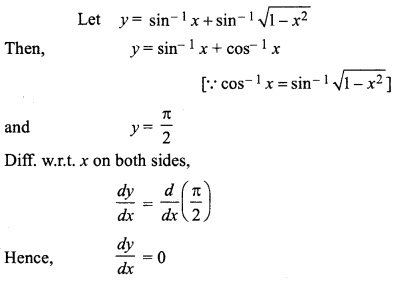
RBSE Solutions For Class 12 Math Question 11.
If cos^-1

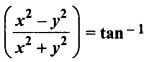
a, then prove that \(\frac { dy }{ dx } \) = \(\frac { y }{ x } \)
Solution:

RBSE Solution Class 12 Maths Question 12.
If, y = x sin (a + y) then prove

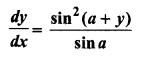
Solution:

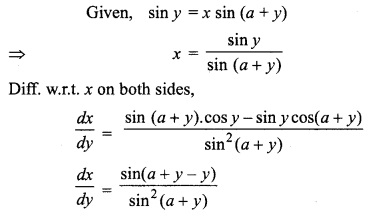
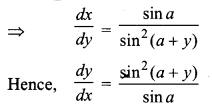
12th Math RBSE Solutions Question 13.
If y = (sin x – cos x)^{(sin x- cos x)} then find \(\frac { dy }{ dx } \)
Solution:
Let y – (sin x – cos x)(sin x – cos)
Taking log on both sides,
log y = (sin x – cos x) log (sin x – cos x)
Diff. w.r.t. x on both sides,

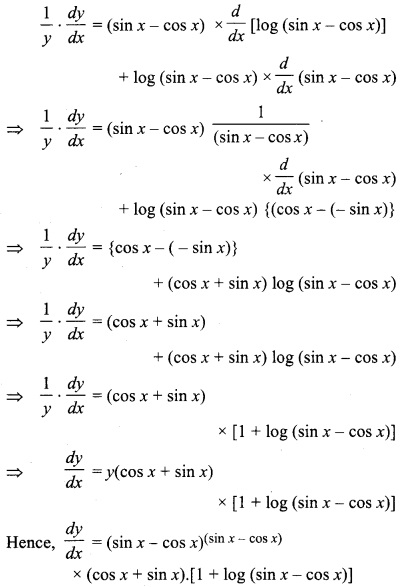
RBSE Solution Class 12th Math Question 14.
If y = sin (sin x), then show that:

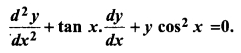
Solution:

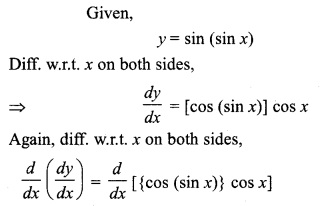
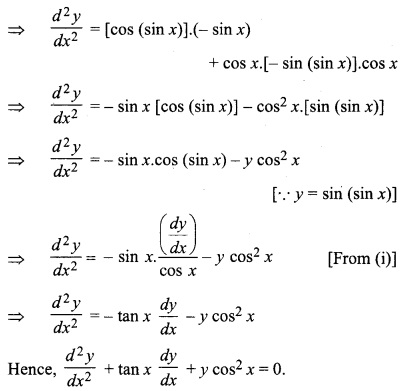
12th Math RBSE Solution Question 15.
(i) If y = e^ax sin bx, then show that

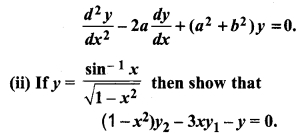
Solution:

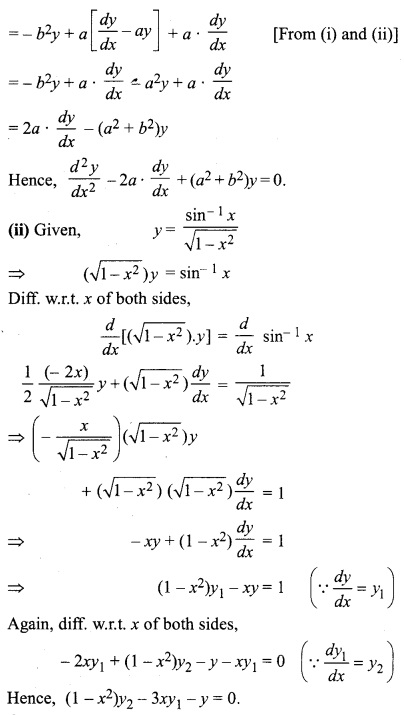
RBSE Solution For Class 12 Maths Question 16.
Prove the Rolle’s theorem for the following :

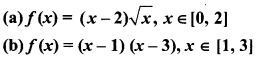
Solution:

which is defined and exist at every point in interval (0, 2).
So, function is differentiable in interval (0, 2).
∵ f(0) = 0 = f(2)
⇒ f(0) = f(2)
Here,f(x) satisfies Rolle’s theorem in given interval.

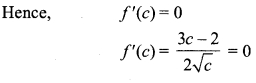
(b) Given f(x) = (x – 1) (x – 3), x ∈ [1, 3]
Here, f (x) is continuous in interval [1, 3] and f'(x) = 2x – 4, which is defined and exist at every point in interval (1, 3). So,f(x) is differentiable in interval (1, 3).
∵ f(1) = 0 = f(3)
⇒ f(1) = f(3)
Here,f(x) satisfies Rolle’s theorem in given interval.
Hence f'(c) = 0
f'(c) = 2c – 4 = 0
⇒ 2c = 4
⇒ c = 2
∴ c = 2 ∈ (1,3)
such that
f'(c) = 0
Hence, Rolle’s theorem verified for c = 2.

Question 17.
Verfiy the Langrange’s theorem for the following:

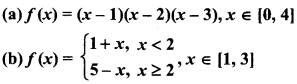
Solution:
(a) Given function
f(x) = (x – 1) (x – 2) (x – 3), x ∈ [0, 4]
⇒ f(x) = x³ – 6x² + 11x – 6, x ∈ [0, 4]
Clearly,f(x) is continuous in intemval [0,4] and f'(x) is defined and exists in interval (0,4). Hence, function satisfies Lagrange’s mean value theorem.


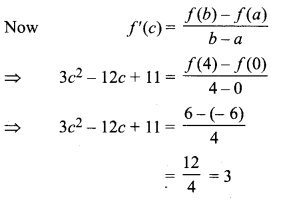
Hence,f(x) is continuous and differentiable in interval (1, 3) excepting x = 2.

So, function f(x) is not differentiable at x = 2.
Here condition for Lagrange’s theorem does not satisfied. Hence, Lagrange’s does not verified.

RBSE Solutions for Class 12 Maths