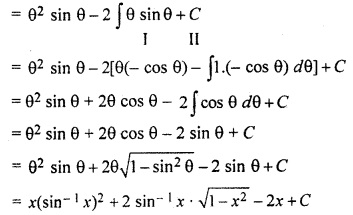Rajasthan Board RBSE Class 12 Maths Chapter 9 Integration Ex 9.6
Exalnate the following :
RBSE Solutions For Class 12 Maths Chapter 9.6 Question 1.
(a) ∫ x cos x dx
(b) ∫ x sec2 x dx
Solution :
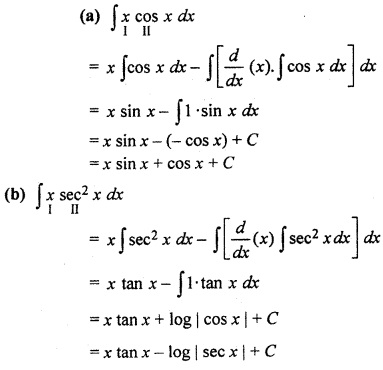
RBSE 12th Maths 9.6 Solution Question 2.
(a) ∫ x3 e-x dx
(b) ∫ x3 sin x dx
Solution:
![]()
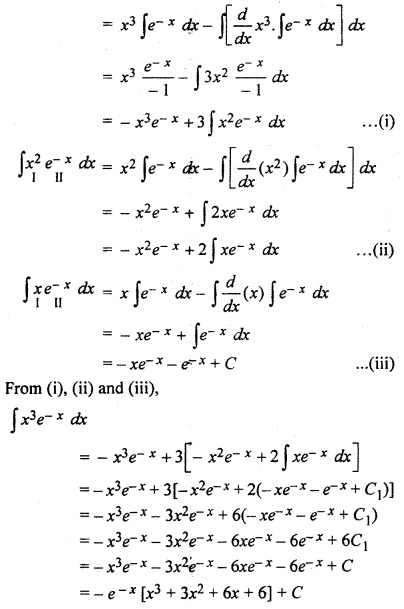
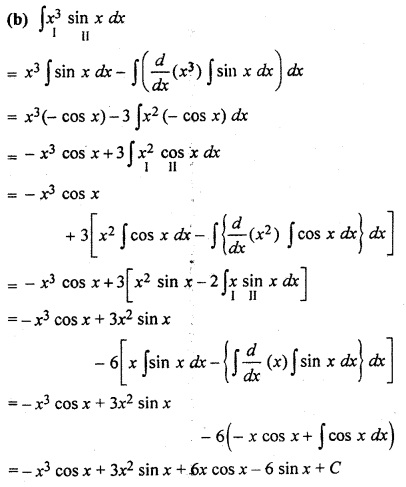
Ex 9.6 Class 12 RBSE Question 3.
(a) ∫ x3 (log x)2 dx
(b) ∫ x3 ex2 dx
Solution:
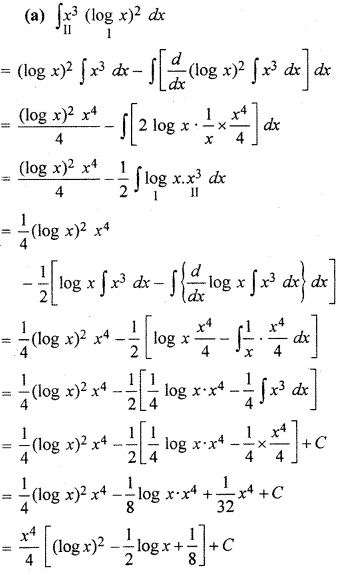
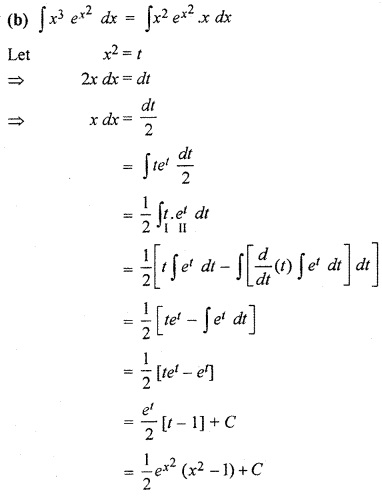
Exercise 9.6 Class 12 Maths RBSE Question 4.
(a) ∫ e2x eex dx
(b) ∫ (log x)2 dx
Solution:
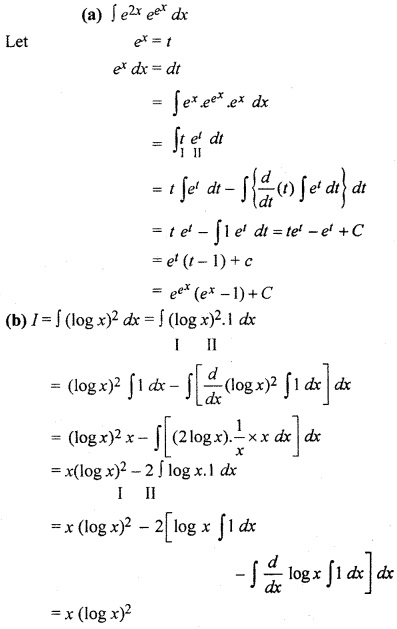
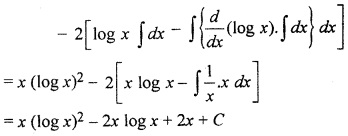
RBSE Solutions For Class 12 Maths Chapter 9 Question 5.
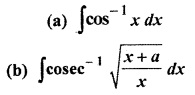
Solution:
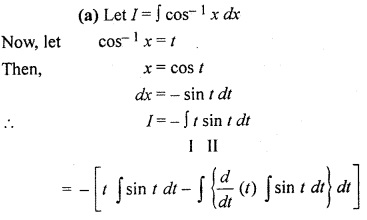
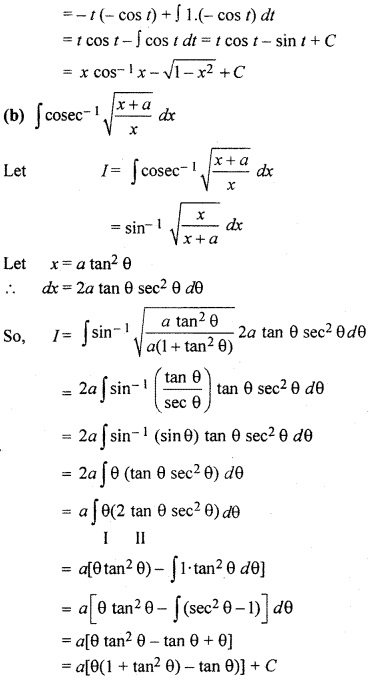
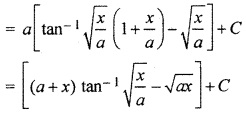
9.6 Class 12 Maths RBSE Question 6.
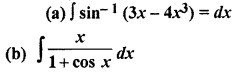
Solution:
(a) Let I = ∫ sin-1 (3x – 4x3) dx
Now, let x = sin t, then dx = cos t dt
∴ I = ∫ sin-1 (3 sin t – 4 sin3 t).cos t dt
= ∫ sin-1 (sin 31) cos t dt
= ∫ 3t cos t dt
= ∫ 3t cos t dt
I II
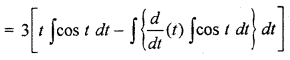
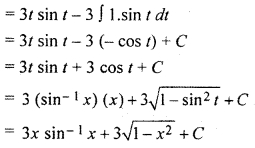
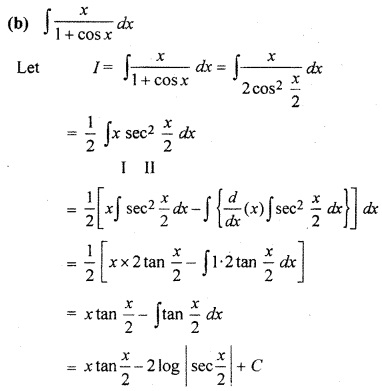
RBSE Class 12 Maths Chapter 9 Solution Question 7.
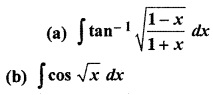
Solution:

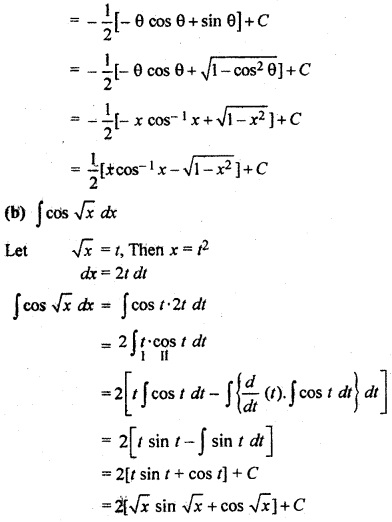
RBSE Solutions For Class 12 Maths Chapter 9.6 Question 8.
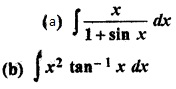
Solution:
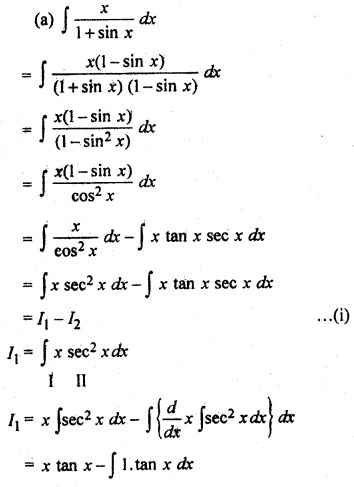
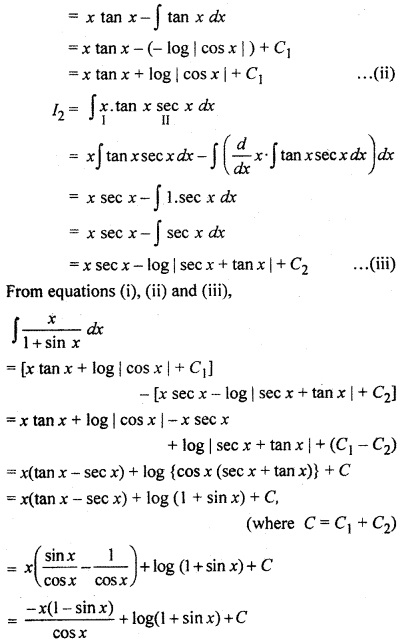
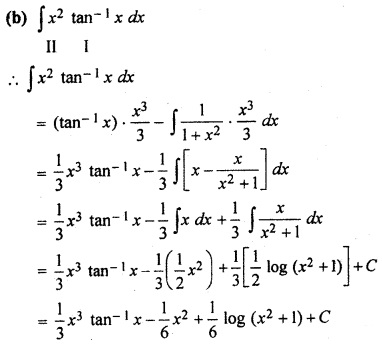
RBSE Class 12 Maths Solutions Question 9.
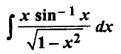
Solution:
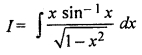
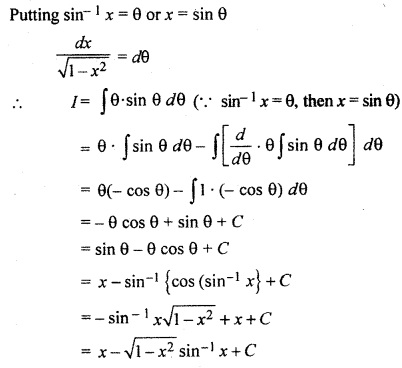
RBSE Class 12th Maths Solution Question 10.
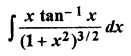
Solution:
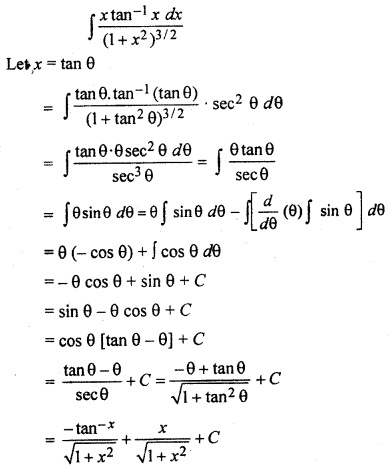
Ex 9.6 Class 12 Question 11.
∫ ex (cot x + log sin x) dx
Solution:
Let I = ∫ ex [log | sin x | + cot x] dx
= ∫ ex log | sin x | dx + ∫ ex cot x dx
= ∫ log | sin x | . ex dx + ∫ ex cot x dx
Now ∫ log | sin x | . ex dx
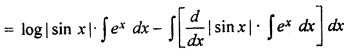
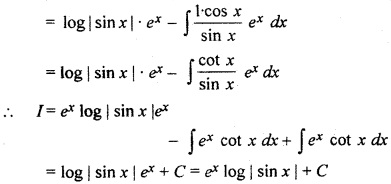
RBSE Solutions For Class 12 Maths Chapter 9.6 Question 12.
![]()
Solution:
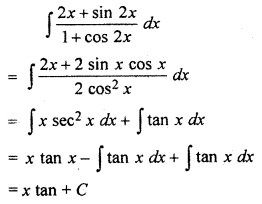
RBSE Solutions For Class 12 Maths Question 13.
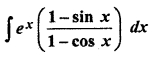
Solution:
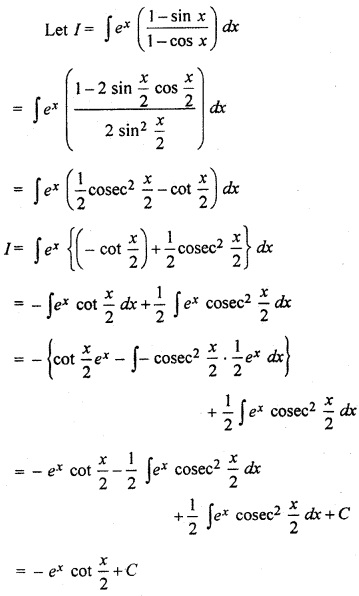
RBSE 12 Maths Solutions Question 14.
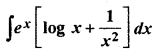
Solution:

RBSE 12th Maths Solution Question 15.
∫ex [log (sec x + tan x) + sec x] dx
Solution:
∫ex [log (sec x + tan x) + sec x] dx
= ∫ex log (sec x + tan x) dx + ∫ex sec x dx
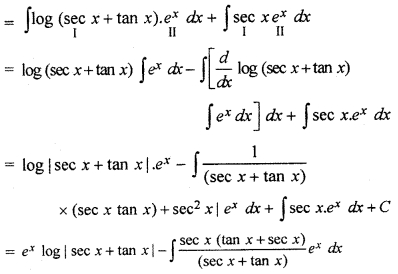
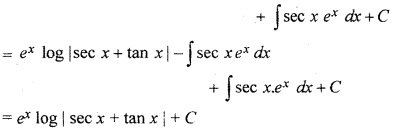
Class 12 Ex 9.6 Question 16.
∫ex (sin x + cos x) sec2 x dx
Solution:
∫ex (sin x + cos x) sec2 x dx
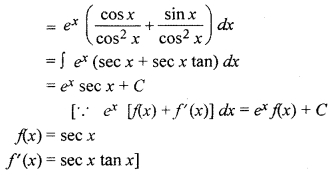
RBSE Maths Solution Class 12 Question 17.
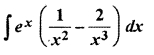
Solution:
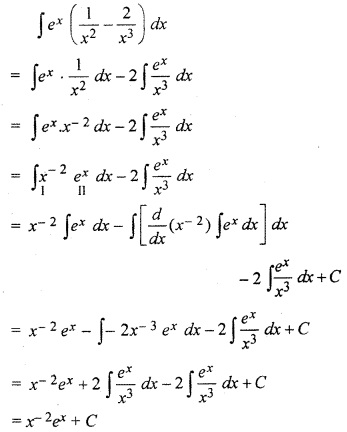
12th RBSE Maths Solution Question 18.
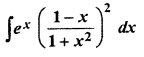
Solution:
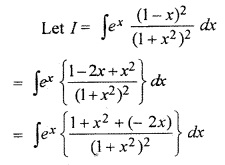
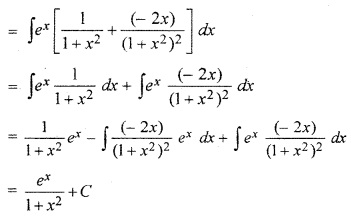
Class 12 Maths RBSE Solutions Question 19.
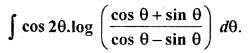
Solution:
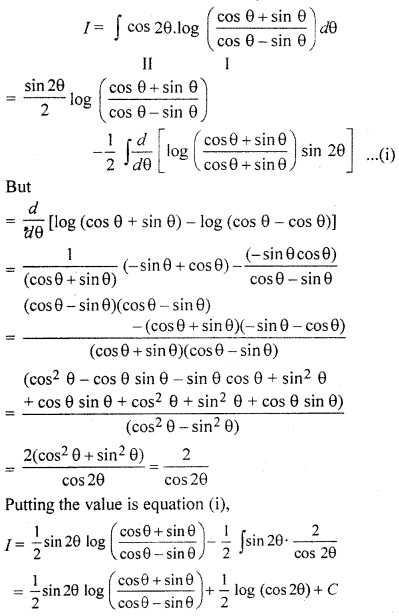
Class 12 RBSE Maths Solutions Question 20.
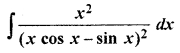
Solution:
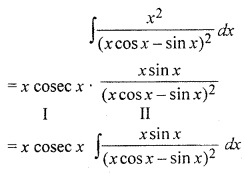
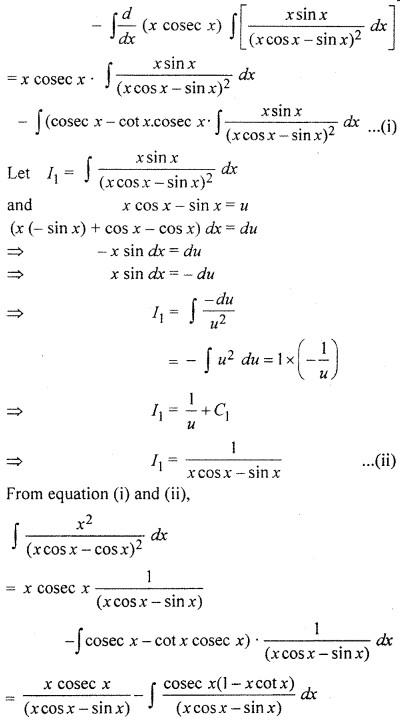
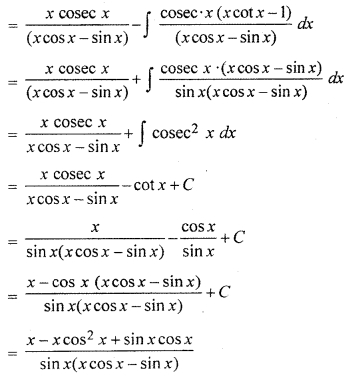
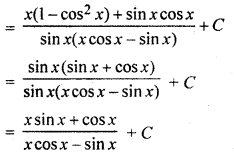
Integration Solution Question 21.
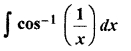
Solution:
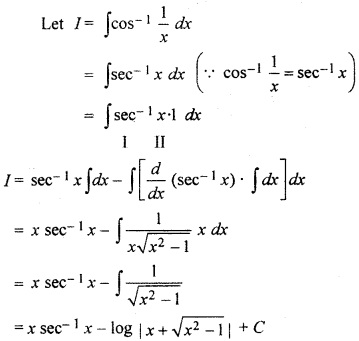
RBSE Solutions Class 12 Maths Question 22.
∫(sin-1 x)2 dx
Solution:
Let I = ∫ (sin-1 x)2 dx
Let sin-1 x = θ
⇒ x = sin θ
∴ dx – cos θ dθ∴
∴ I= ∫θ2 . cos θ dθ
= θ2 sin θ – ∫20 sin θ dθ + C