RBSE Solutions for Class 12 Physics Chapter 5 Electric Current

Rajasthan Board RBSE Class 12 Physics Chapter 5 Electric Current

RBSE Class 12 Physics Chapter 5 Text Book Exercise with Answers

RBSE Class 12 Physics Chapter 5 Multiple Choice Type Questions

RBSE Solutions For Class 12 Physics Chapter 5 Question 1.
The product of resistivity and conductivity of conductor depends upon :
(a) the cross-sectional area
(b) the temperature
(c) the length
(d) none of these
Answer:
(d) none of these

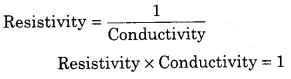
RBSE Solutions For Class 12 Physics Question 2.
Two wires of same shape whose resistivity ρ₁and ρ₂ are connected in series. The equivalent resistivity of the combination will be :
(a) \(\sqrt{p_{1} \rho_{2}}\)
(b) 2 (ρ₁ + ρ₂)
(c) \(\frac{\rho_{1}+\rho_{2}}{2}\)
(d) ρ₁ + ρ₂
Answer:
(c) \(\frac{\rho_{1}+\rho_{2}}{2}\)
Resistance in series

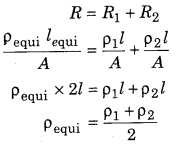
Physics Class 12 RBSE Solutions Question 3.
A conducting resistance is connected to the battery and temperature of conductor decreases by the process of cooling then the value of current will be :
(a) increased
(b) decreased
(c) remain constant
(d) zero
Answer:
(a) increased
The resistance of the conducting wire will decrease according to equation R_t = R₀ (1 ± α Δt) due to which current will increase according to Ohm’s law (I = \(\frac{V}{R}\))

Class 12 Physics RBSE Solutions Question 4.
A cell of e.m.f. 2.1 V gives a current of 0.2 A. This current is passing through the resistance of 10 Ω. The internal resistance of cell is :
(a) 0.2 Ω
(b) 0.5 Ω
(c) 0.8 Ω
(d) 0 Ω
Answer:
(b) 0.5 Ω

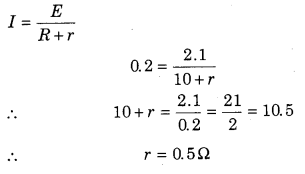
RBSE Solution Physics Class 12 Question 5.
The current I and voltage V curves for a given metallic conductor at two different temperatures T₁ and T₂ are shown in the figure then :

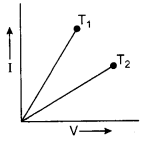
(a) T₁ = T₂
(b) T₁ > T₂
(c) T₁ < T₂
(d) None of these
Answer:
(c) T₁ < T₂
Gradient of graph,
tanθ = \(\frac{1}{R}=\frac{I}{V}\)
But, according to equation R_t = R₀ (1 α Δt)
∴ The resistance R₂ > R₁
∴ T₂ > T₁

RBSE Solution Class 12 Physics Question 6.
The electric power is supplied through the copper wires from a one city to another city which is 150 km apart. If the terminal voltage and average resistance of per kilometer are 8 volt and 0.5 Ω respectively then the power loss in a wire is :
(a) 19.2 W
(b) 19.2 kW
(c) 19.2 J
(d) 12.2 kW
Answer:
(b) 19.2 kW
Total resistance of wire = 0.5 × 150 km = 75 Ω
Potential drop on wire = 8 × 150 = 1200 volt
Power loss m wire (P) = \(\frac{V^{2}}{R}=\frac{1200 \times 1200}{75}\)
= 19200 watts = 19.2 kW

RBSE 12th Physics Solution Question 7.
Five resistances of R Ω were taken. First three resistances are connected in parallel combination and rest two are connected in series combination, then the equivalent resistance is :

Answer:
(b)
Equivalent resistance,

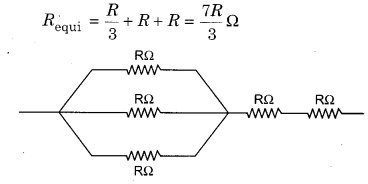
RBSE Solutions Physics Class 12 Question 8.
Drift velocity (v_d) depends upon the electric field, in which the following dependence of drift velocity on the electric field obey the ohm’s law is :
(a) v_d ∝ E²
(b) v_d ∝ E
(c) v_d ∝ E^1/2
(d) v_d = constant
Answer:
(b) v_d ∝ E

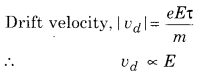
RBSE Solution Class 12th Physics Question 9.
A carbon resistance has a colour sequence of bands as blue, yellow, red and silver. The value of resistance is :
(a) 64 × 10² Ω
(b) (64 × 10² ± 10%) Ω
(c) 642 × 10⁴Ω
(d) (26 × 10³ ± 5%) Ω
Answer:
(b) (64 × 10² ± 10%) Ω

12th Physics Solution RBSE Question 10.
When the wire is connected with a battery is heated up due to electric current which quantity do not vary :
(a) Drift velocity
(b) Resistivity
(c) Resistance
(d) Number of free electrons
Answer:
(d) Number of free electrons
Number of free electrons does not depend on temperature.

RBSE Class 12 Physics Chapter 5 Very Short Answer Type Questions

Class 12 RBSE Physics Solution Question 1.
Calculate the resistance of resistor by V-I curve

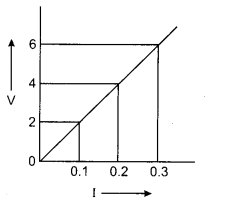
Answer:

Physics Solution Class 12 RBSE Question 2.
Write the S.I. unit of current density?
Answer:
Current density, J =\(\frac{I}{A}\) = Ampere/metre²

RBSE Solution Of Class 12th Physics Question 3.
Write the relation between conductivity and current density?
Answer:
Conductivity \(\vec{J}=\sigma \vec{E}\)

RBSE Solutions 12 Physics Question 4.
Write the two examples of non-ohmic resistance?
Answer:
Diode and electrolytes.

RBSE Solutions Of Class 12 Physics Question 5.
Write the dependency of resistivity of metals on temperature?
Answer:
Resistivity of a conductor depends upon temperature as
ρ = ρ₀(l + α Δt)

12th RBSE Physics Solution Question 6.
Write the name of two substances of which when its temperature increases its resistivity decreases.
Answer:
The resistivity of semiconductor decreases with increase in its temperature. So the examples are Germanium and Silicon.

Question 7.
Find the value of current which is flowing through the bulb of 40 W 220 V.
Answer:

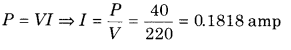
RBSE Class 12 Physics Chapter 5 Short Answer Type Questions

Question 1.
What will be the value of charge when an electric current flows through a conductor?
Answer:
On flowing a electric current in conductor it does not charged. So total charge across it will be zero.

Question 2.
In the given material the resistivity of single metal are ρ₁ and ρ₂ (Ω × m), find the ratio of ρ₁ and ρ₂.
Answer:
Resistivity of a conductor does not depend on length and area of cross section of the material.
∴ ρ₁ : ρ₁ = 1 : 1

Question 3.
Two identical cells having equal emf and negligible internal resistance are combined in parallel combination. Find out the electric current in resistance R:

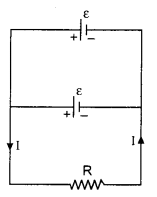
Answer:
In parallel combination the potential difference will be equal.
V = E
∴ Current, I = \(\frac{V}{R}\)
∴ I = \(\frac{E}{R}\)

Question 4.
What is the difference between emf and terminal potential difference?
Answer:
See the article no. 5.10.
Electromotive Force (or e.m.f.) of a Cell
“The energy given by the cell to a unit charge for flowing through the circuit i.e., the work done in flowing the unit charge through the complete circuit by the cell is called the electromotive force or e.m.f. of the cell.”
It is represented by E. Therefore
E = \(\frac{W}{q}\) ……………. (1)
Where W is the work done by the cell in flowing charge q throughout the circuit.
∴ Unit of E = —\(\frac{\mathrm{J}}{\mathrm{C}}\) = JC^-1 or volt.
If q = 1C, W = 1J, then E = 1JC^-1
i. e., “If the work done in flowing unit charge is lJ then the e.m.f. of the cell is 1 JC^-1 or 1 volt.”
The value of e.m.f. for one cell is constant and different for different cells. For example, e.m.f. of voltaic cell is 1.08 volt, for daniell cell it is 1.12 volt and for dry cell it is 1.5 volt.
Important Points
1. Although we call e.m.f. as force but actually it is energy which is given by the cell to unit charge for flowing through the circuit.
2. If external resistance is connected between the terminals of the cell the the potential difference between the terminals is ‘Terminal voltage’ of the cell.

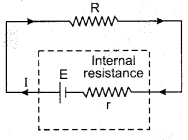
3. When there is no external resistance connected between the terminals the potential difference is equal to the e.m.f. of the cell.

Terminal Potential Difference
“Work done by the cell in flowing a unit positive charge from one terminal to other terminal through external resistance in a circuit is called the terminal potential difference or terminal voltage of the cell.”
Therefore terminal voltage
V = \(\frac{W_{\mathrm{ext}}}{q}\) …………… (2)
Where W_ext is the work done by the cell in flowing q charge through external circuit.
If R be external resistance in the circuit and i the flowing current, then
V = \(\frac{W_{\mathrm{ext}}}{q}\) = iR (according to Ohm’s law)
Similarly if r be the internal resistance of the cell, then the potential drop i.e., the energy consumed due to internal resistance r,
v = ir
According to definition of e.m.f.
E = Work done (external work + internal work) in flowing unit charge.

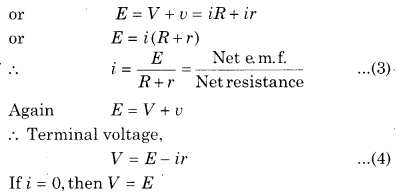
i.e., “in open circuit, the terminal potential difference of the cell is called the e.m.f. of the cell.”
From equation (4),

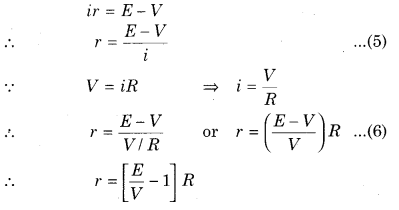
Therefore, internal resistance of a cell can be obtained with the help of equations (5) and (6).

Question 5.
Write the definition of drift velocity.
Answer:
Drift Velocity (v_d)
When a potential difference (V) is applied across the conductor of length (l), then an electric field \(\overrightarrow{(E)}\) develops in the conductor \(\left(E=\frac{V}{l}\right)\) Due to this field each free electron of the conductor experiences an electric force \(\vec{F}=-e \vec{E}\) towards the positive end of the conductor and hence it starts accelerated motion \(\left(\vec{a}=\frac{\vec{F}}{m}\right)\) towards the positive end. During its accelerated motion it collides with the other electrons and positive ions of the conductor. Therefore its velocity always remains changing. This motion of electron is known as ‘Drift motion’ and the average velocity between two successive collisions is known as ‘Drift velocity.’ It is denoted by v_d.

“i.e., the maximum velocity achieved by the electrons due to imposed electric field with which they collide with other ions, is known as drift velocity.” Time taken in two successive collisions is called ‘Relaxation time’. For most of the conductors, the relaxation time is the order of 10^-14s. Just before colliding with a ion, the velocity is maximum and after collision for a moment the velocity becomes zero. Again electron gets accelerated by applied electric field and repeats the previous situation of colliding with ions of the conductor. Thus “the potential difference of battery does not provide accelerated motion to electrons but it can provide a small constant velocity along the length of the conductor, which is imposed upon the random motion of the electrons. This constant velocity of the electron is called drift velocity of electrons.” The order of this drift velocity about 10^-4 m/s.

Reason of small value of drift velocity : In following figure 5.4, the random motion of electron is shown by thick lines and in presence of external electric field by dotted lines. It is obvious from the figure that the electron moves with small drift velocity and due to this reason point X is shifted to X’. Thus due to electric field, the net displacement becomes XX’. Which has very small value. This is why the drift velocity is very small.

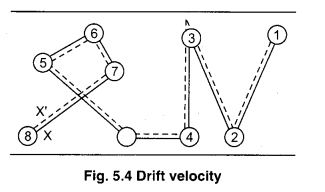
Relaxation time (τ) : The average time taken by electron in two successive collisions is known as ‘Relaxation time’ and it is denoted by τ. It is obtained by

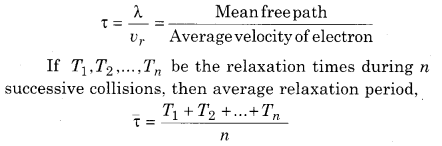
Question 6.
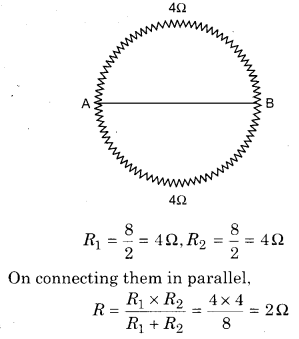
When a wire of 80 resistance is bent in the form of a circle then find out the resistance between any two ends of the diameter.
Answer:
When resistor is folded into the circular form, then across diameter, for equivalent resistance, shape is divided in two parts, therefore resistance becomes half.

Question 7.
What will be the effect on resistance and resistivity on produce the distortion in the size of a matter?
Answer:
Resistance is inversely proportional to area of cross-section of the substance while there is no effect on resistivity.

Question 8.
Can the potential difference between the plates of a cell more than its electromotive force (emf)?
Answer:
Yes, when the cell is in condition of charging.
V_T = E + Ir

RBSE Class 12 Physics Chapter 5 Long Answer Type Questions

Question 1.
What is called drift velocity? Obtain the equation of Ohm’s law (\(\vec{J}=\sigma \vec{E}\)) on the basis of drift velocity where parameters are in their usual meaning.
Answer:
When a potential difference (V) is applied across the conductor of length (l), then an electric field \(\overrightarrow{(E)}\) develops in the conductor \(\left(E=\frac{V}{l}\right)\) Due to this field each free electron of the conductor experiences an electric force [latex]\vec{F}=-e \vec{E}[/latex] towards the positive end of the conductor and hence it starts accelerated motion \(\left(\vec{a}=\frac{\vec{F}}{m}\right)\) towards the positive end. During its accelerated motion it collides with the other electrons and positive ions of the conductor. Therefore its velocity always remains changing. This motion of electron is known as ‘Drift motion’ and the average velocity between two successive collisions is known as ‘Drift velocity.’ It is denoted by v_d.

The relation between drift velocity and potential difference,
v_d = \(\frac{e \tau}{m} \frac{V}{l}\) …………… (1)
and relation between drift velocity and electric current,
v_d = \(\frac{i}{A n e}\) ………….. (2)
On comparing equations (1) and (2) we have

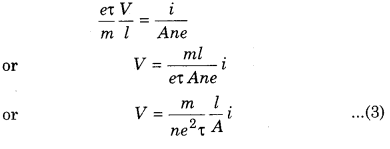
or V = ρ \(\frac{l}{A}\) i ………….. (4)
Here \(\frac{m}{n e^{2} \tau}\) which is characteristic of the substance of the conductor and it is called ‘specific resistance’ or ‘resistivity’ of the substance. It is constant for one substance and different for different substances.

If physical conditions of the conductor do not change at constant temperature, then l and A will also remain constant. Therefore,
ρ\(\frac{l}{A}\) = constant = R (Resistance of the conductor)
∴ From equation (4),
V = Ri …………….. (5)
or V ∝ i
i.e., “the potential difference developed across a conductor is directly proportional to current flowing through the conductor provided the physical conditions of the conductor remain unchanged.” This is Ohm’s law.
Vector form of Ohm’s law :
From equation (3),

Equation (7) is called microscopic form of Ohm’s law.
Specific Resistance. “Ratio of intensity of electric field (E) and current density (J) at any point inside the current carrying conductor, is called the specific resistance of the material of the conductor. It is represented by ρ.”
∴ ρ = \(\frac{E}{J}\)
If the length of the conductor be l and potential difference across it be V, then
E = \(\frac{V}{l}\) and j = \(\frac{i}{A}\)
Where A is the area of cross-section of the conductor

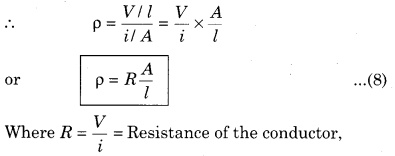
If A = 1 m²; l = 1 m, then ρ = R
i.e., “the specific resistance of a material is equal to the resistance of material when the length and area of cross-section of material take as unity.”

Specific resistance can also be obtained by following formula,
ρ = \(\frac{m}{n e^{2} \tau}\) …………….. (9)
Where m is the mass of electron, n is the free electron density, e is the electronic charge and τ is the relaxation time.

Question 2.
Establish the relation between drift velocity and electric field. What is mobility? Describe the relation between mobility and velocity.
Answer:
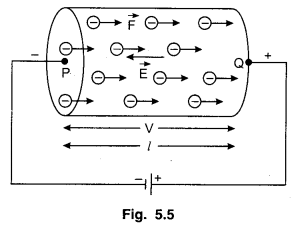
Relation between Drift Velocity and Potential Difference
Suppose PQ is a conductor of length l and a potential difference V is applied across PQ as shown in the figure 5.5. i.e., its P end remains negative and Q end positive. Therefore an electric field is developed directing from Q to P and its intensity is given by
E = \(\frac{V}{l}\) …………. (1)
Each free electron of the conductor experiences a force (\(\vec{F}\)) towards the end Q,
∴ \(\vec{F}=-e \vec{E}\)

If m be the mass of the electron, then its acceleration

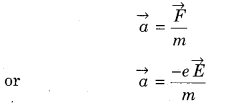
∵ The average thermal velocity of electrons is zero.
∴ u = 0
Therefore using first equation of motion (v = u + αt), we have

This is the relation between drift velocity and potential difference.

Mobility
In the expression of drift velocity (speed), the term \(\left(\frac{e \tau}{m}\right)\) is constant because e and m are constant and τ is the characteristics of specific metal, so for specific metal at constant temperature τ is constant.
Constant term \(\left(\frac{e \tau}{m}\right)\) for a given metal is called mobility (μ).

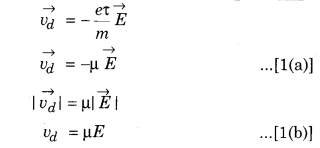
For specific metal, v_d ∝ E
Magnitude of drift velocity is directly proportional to the applied electric field

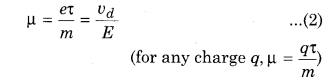
So the mobility of ions are defined as the ratio of drift velocity to the electric field.
Mobility is positive and its unit is \(\frac{\mathrm{m} / \mathrm{s}}{\mathrm{volt} / \mathrm{m}}\) = m²s^-1volt^-1
When electric field is same for given metals
\(\frac{\mu_{1}}{\mu_{2}}=\frac{v_{d_{1}}}{v_{d_{2}}}\)
It means when in any metal drift speed is more than electrons, then its mobility will also high. We will discuss about mobility related to semiconductor in Chapter 16.
Relation between electric current and mobility for semiconductor : Conductivity in semiconductors is due to electrons and holes both.

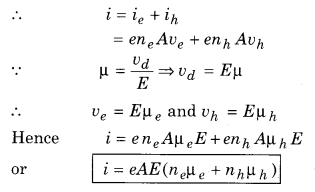
Question 3.
Establish the relation between resistance and resistivity. How does resistivity depend on the temperature? Describe conductors, insulators and semiconductors on the basic of resistivity.
Answer:
Resistivity
On practical basis it is found that the resistance depends upon the length l and area of cross-section A of the resistor as under
R ∝ \(\frac{l}{A}\)
or R = ρ\(\frac{l}{A}\)
where ρ = specific resistance or resistivity of the material of the conductor. It is the characteristic of the conductor.
Special fact : Resistivity does not depend upon the dimensions of the conductor i. e., it does not depend upon the length and area of cross-section of the conductor.

Effect of temperature on resistivity of metallic conductors : Specific resistance is given by,
ρ = \(\frac{m}{n e^{2} \tau}\) ……………. (1)
Where, m = mass of electron
e = charge of electron
n = number of free electrons per unit volume
τ = relaxation time
In equation, there is no effect of increase in temperature on m and e. If temperature rise is not much, then n will also remain unchanged. Now we have to study the effect of rise in temperature on relaxation time τ.
∵ τ = \(\frac{\lambda}{v_{\mathrm{rms}}}\)
Where λ is mean free path and v_rms is the root mean square velocity of electrons.

When the temperature is increased, then the vibrational energy of atoms of the conductor increases and hence their amplitude of vibration increases and as result the value of mean free path λ decreases. Also due to increase in temperature the value of v_rms increases. Hence due to combined effect of decrease in λ and increase in v_rms, the relaxation time x will decrease. Thus it is clear from equation (1) the resistivity ρ will increase. Thus the specific resistance increases with increase in temperature. The change in resistivity (ρ) with rise in temperature is given by following relation,
ρ_t = ρ₀(1 + αt) ………….(2)
Where ρ_t = Specific resistance at t°C
ρ_o = specific resistance at 0°C
α = linear temperature coefficient of resistance The variation in resistivity of metallic conductors with temperature is shown in figure 5.11.

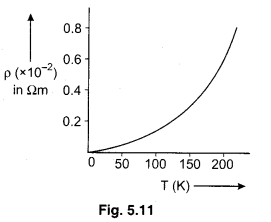
Temperature dependence of resistivity of semiconductor and insulator : Change in resistivity of semiconductor and insulator is different from change in resistivity of metallic conductors. For conductors the change in resistivity with temperature is linear but the change in resistivity of insulator
and semiconductor is represented by exponential curve as shown figure 5.13.

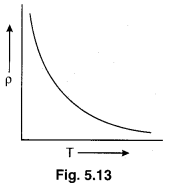
The mathematical variation of specific resistance with temperature
ρ_t = ρ₀(1 – α Δt)
Linear temperature coefficient of resistivity is negative for semiconductor and conductors.
Resistivity of a semiconductor varies with temperature according to following relation :
\(\rho_{t}=\rho_{0} e^{-\left(\frac{E_{g}}{k T}\right)}\) …………. (3)
Where ρ_t = Resistivity at t°C
ρ₀ = Resistivity at 0°C
E_g = Energy gap
k = Boltzmann constant
T = (273 + t°C) K

Question 4.
Two cells of emf E₁ and E₂ and internal resistance r₁ and r₂ respectively are connected in parallel combination. Determine the equivalent emf and equivalent internal resistance of the combination.
If this combination is connected with external resistance R, then obtain the value of current flowing in this external resistance.
Answer:
Parallel Combination of Cells
(a) When e.m.f. and internal resistance is same for all cells : Suppose n cells of same e.m.f. E and internal resistance r are joined in parallel and this combination is connected with external resistance R as shown in the figure 5.19. All the cells are connected between junctions A and B. Any charge flowing in the circuit, passes only one cell. Therefore the equivalent e.m.f. = E = e.m.f. of one cell

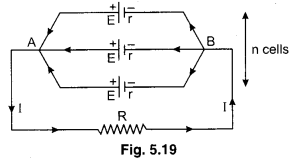
The equivalent internal resistance

then the combination is significant.
(b) When the e.m.f. and internal resistance of the cells are different :
When the positive terminals of all cells are connected to one point and all their negative terminals to another point, the cells are said to be connected in parallel.

As shown in figure 5.20, suppose two cells of emf’s ε₁ and ε₂ and internal resistances r₁ and r₂ are connected in parallel between two points A and B.

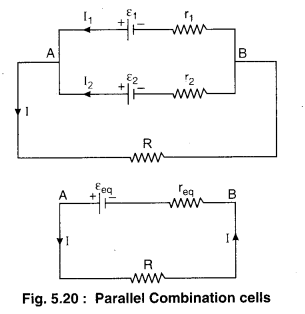
The end points of A and B are connected with external resistance R.
If in each cell current is I₁ and I₂ respectively then total current in external resistance is
I = I₁ + I₂ ……………… (1)
If terminal potential between A and B is V.
For I cell V = ε₁ – I₁r₁ …………… (2)
For II cell V = ε₂ – I₁₂r₂ ………….. (3)
From above equations.

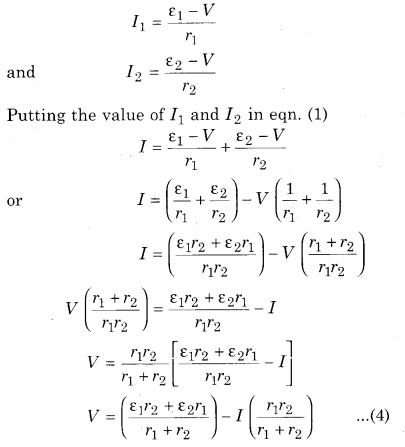
If equivalent e.m.f. is ε_eq and equivalent internal resistance is r_eq of combination then terminal potential difference will be
V = ε_eq – Ir_eq …………… (5)
Comparing equation (4) and (5),

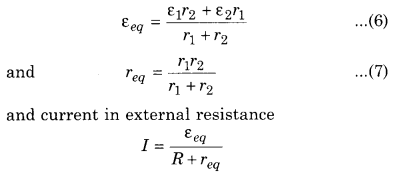
By use of parallel combination it is clear :
(i) When ε₁ = ε₂ = ε and r₁ = r₂ = r means two cells of equal emf and equal internal resistance are connected in parallel then ε_eq = ε and r_eq = \(\frac{r}{2}\)

(ii) When n cells of equal emf and equal internal resistance are connected in parallel combination
than ε_eq = ε and r_eq = \(\frac{r}{n}\) then electric, current in external resistance will be
I = \(\frac{\varepsilon}{R+r / n}\) ………………….. (8)
(iii) We can display equations (6) and (7) in the below form

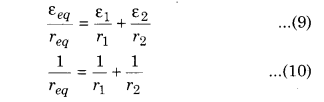
Similarly if n cells are combined in parallel system then,

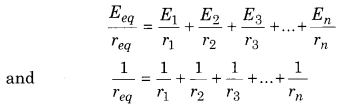
RBSE Class 12 Physics Chapter 5 Numerical Questions

Question 1.
The length of cylindrical metal (copper) is 1 cm and radius is 2.0 mm. If 120 V potential difference is applied across the ends of the rod then find out the electric current flowing through it. (Resistivity of copper is 1.7 × 10^-8 Ω-m)
Solution:
Length (l) = 1 cm = 1 × 10^-2 m
Radius (r) = 2 mm = 2 × 10^-3 m
Area of cross section of wire
(A) = πr² = π ×(2 × 10^-3)² = 4π × 10^-6 m²
Potential across ends (V) = 120 V
Current (I) = ?
According to the Ohm’s law

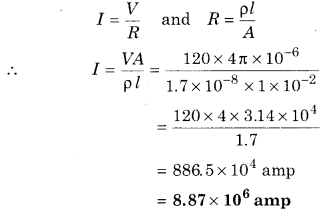
Question 2.
Find out the equivalent resistance between a and b as shown in figure.

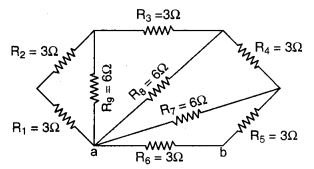
Solution:
Adding R₁ and R₂ in series
R’ = R₁ + R₂ = 6Ω
Adding R’ and R₉ in parallel

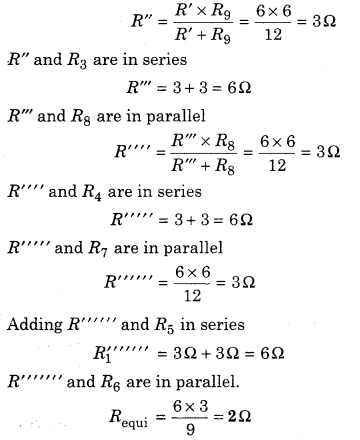
Question 3.
Find out the equivalent resistance between a and b of the circuit in which infinite resistances are connected.

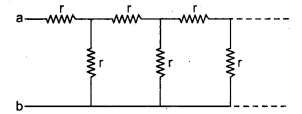
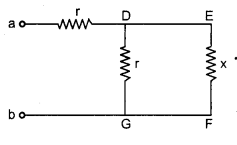
Solution:
Let except first two resistances the equivalent resistance of all be x. Adding DG and EF resistance in parallel.

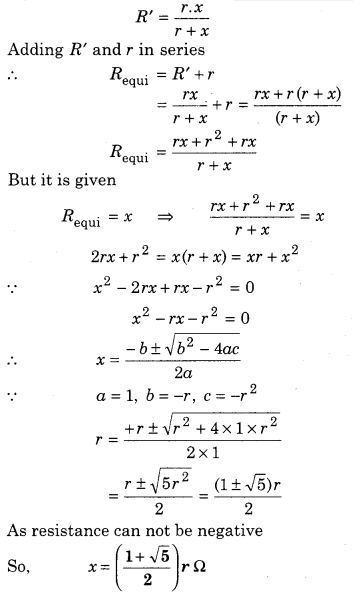
Question 4.
Three resistances of 1 Ω, 2 Ω and 3 Ω are connected in series combination. Find out equivalent resistance of the combination. If this combination is connected by the battery of 12 V e.m.f. and negligible internal resistance then find out the voltage across each ends of resistance.
Solution:
Connecting 1 Ω, 2 Ω and 3 Ω in series
R_equi = R₁ + R₂ + R₃ = 1 + 2 + 3 = 6 Ω
Current flowing in circuit

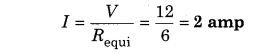
Potential on 1 Ω resistance = V = IR = 2 × 1 = 2V
Potential on 2 Ω resistance V = IR = 2 × 2 = 4V
Potential on 6 Ω resistance (V) = IR = 2 × 3 = 6V

Question 5.
At room temperature (27°C) the resistance of thermal element is 100 Ω. If resistance of thermal element is 117 Ω, then find out the temperature of the element. Temperature coefficient of resistance of resistor is [1.70 × 10^-4 C^-1].
Solution:

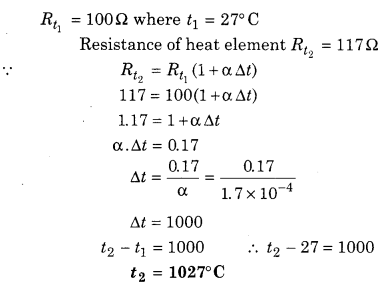
Question 6.
A wire having length 15 m and 6 × 10^-7 m² cross-sectional area in which a negligible current is flowing, its resistance is 5 Ω. What is the resistivity of the substance at experimental temperature?
Solution:
Length of wire (l) = 15 m
Area of cross-section (A) = 6.0 × 10^-7 m²
Resistance (R) = 5.0Ω

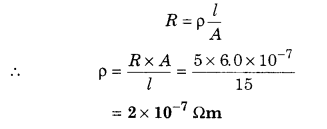
Question 7.
The current of 0.5 Amp is flowing in a copper wire whose cross-sectional area is 1mm². If the number of free electrons is 8.5 × 10²² per cm³ in unit volume then find out the drift velocity of electrons?
Solution:
Area of cross section = 1 mm²
= 1 ×(10³)² = 1 × 10^-6 m²
Number of free electrons (n) = 8.5 × 10²² / cm³
= 8.5 × 10²⁸/m³
Current (I) = 0.5 amp

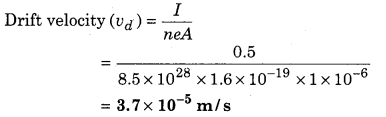
Question 8.
At what temperature the resistance of copper wire becomes doubled than the resistance of the wire at 0°C? Temperature coefficient of resistance is 4.0 × 10^-30°C^-1.
Solution:
Given : R_t = 2R,
R_t = R₀ (1 + α Δt)
2R₀ = R₀ (1 + α Δt)

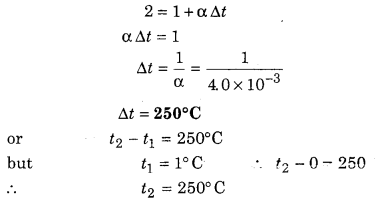
Question 9.
E.m.f. of accumulator battery of car is 12 V and its internal resistance is 0.4 Ω, then find out the maximum current drawn from the battery.
Solution:
Electromotive force (E) = 12 V
Internal resistance (r) = 0.4 Ω

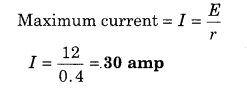
Question 10.
A coil which has a resistance of 4.2 Ω is immersed into water. If 2A current is flowing through it for 10 min then how much heat will produce in calorie?(</ = 4.2 J/cal)
Solution:
Given, R = 4.2 Ω, I = 2 Amp.
t = 10 minute = 10 × 60 = 600 sec
energy E = W = I²Rt
= (2)2 × 4.2 × 600 Joule
But W = JQ

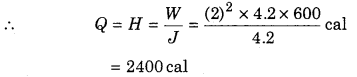
Question 11.
The length of a cylindrical tube is / and its internal and external radius are a and b respectively. If resistivity of matter is ρ then find out the resistance between the ends of the tube.
Solution:
Resistance of cylinder, R = ρ\(\frac{l}{A}\)
Area of cross section for flow of current = External area – Internal area

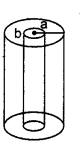
= πa² – πb²
= π (a² – b²)
∴ R = \(\frac{\rho l}{\pi\left(a^{2}-b^{2}\right)}\)

Question 12.
In a house 4 bulbs of 100 W and 4 bulbs of 40 W glows daily for 4 hours and 6 hours respectively.
Two fans of 60 W running daily for 8 hours. Find out the consumption of electricity in one month of 30 days. If rate of consumption of electricity is ? 5 per unit.
Solution:
Energy consumed by 4 bulbs of 100 watt each.

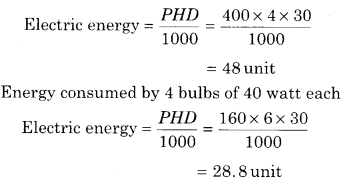
Energy consumed by 2 fans of 60 watt each

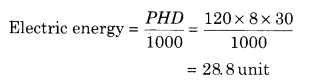
Total consumed electric energy = 48 + 28.8 + 28.8 = 105.6 unit
Energy consumed = Electric energy × rate per unit
= 105.6 × 5 = 528.00 = ₹ 528

RBSE Solutions for Class 12 Physics