RBSE Solutions for Class 7 Maths Chapter 4 परिमेय संख्याएँ Ex 4.1 is part of RBSE Solutions for Class 7 Maths. Here we have given Rajasthan Board RBSE Class 7 Maths Chapter 4 परिमेय संख्याएँ Exercise 4.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 7 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | परिमेय संख्याएँ |
| Exercise | Ex 4.1 |
| Number of Questions | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 7 Maths Chapter 4 परिमेय संख्याएँ Ex 4.1
प्रश्न 1
निम्नलिखित परिमेय संख्याओं के समतुल्य पाँच-पाँच परिमेय संख्याएँ लिखिए।
![]()
हल:
(i) –\(\frac { 2 }{ 3 }\) के समतुल्य पाँच परिमेय संख्याएँ
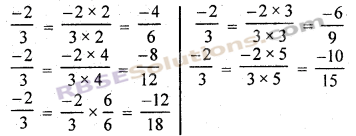
(ii) \(\frac { 1 }{ 5 }\) के समतुल्य पाँच परिमेय संख्याएँ

(iii) \(\frac { -5 }{ 3 }\) के समतुल्य पाँच परिमेय संख्याएँ निम्न हैं

(iv) \(\frac { 4 }{ -9 }\) के समतुल्य पाँच परिमेय संख्याएँ निम्न हैं
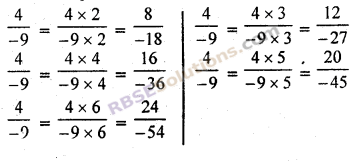
![]()
प्रश्न 2
\(\frac { -5 }{ 12 }\) की तीन(RBSESolutions.com)ऐसी समतुल्य परिमेय संख्याएँ लिखिए जिनका हर क्रमशः 60, – 96 व 108 हो।
हल:
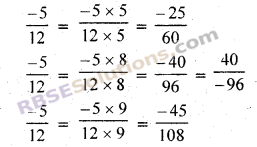
प्रश्न 3
\(\frac { -3 }{ 7 }\) की तीन ऐसी समतुल्य परिमेय संख्याएँ लिखिए जिनका अंश क्रमशः 24, – 60 व 75 हो।
हल:
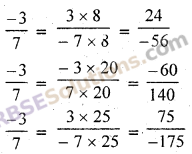
![]()
प्रश्न 4
निम्नलिखित परिमेय संख्याओं को उनके सरलतम रूप (मानक रूप) में लिखिए।
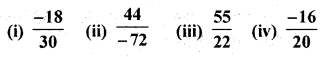
हल:

![]()
प्रश्न 5
निम्नलिखित परिमेय संख्याओं को संख्या रेखा पर निरूपित कीजिए।
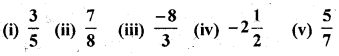
हल:
(i) हम जानते हैं कि \(\frac { 3 }{ 5 }\) शून्य से बड़ा है और 1 से कम है। अत: भिन्न \(\frac { 3 }{ 5 }\) , 0, और 1 के बीच में होगी।
अब हमें \(\frac { 3 }{ 5 }\) ई को दर्शाना है, इसलिए(RBSESolutions.com)हम 0 और 1 के बीच की दूरी को पाँच बराबर भागों में बाँटते हैं। इसके तीसरे भाग पर बिन्दु P अंकित करते हैं।
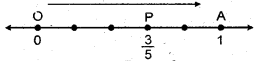
इस प्रकार संख्या रेखा पर बिन्दु P, \(\frac { 3 }{ 5 }\) को दर्शाता है।
(ii) हम जानते हैं कि \(\frac { 7 }{ 8 }\) शून्य से बड़ा है और 1 से कम है।
∴ भिन्न \(\frac { 7 }{ 8 }\),0 व 1 के बीच में होगी।
अब हमें \(\frac { 7 }{ 8 }\) को दर्शाना है इसलिए हम 0 और 1 के बीच की दूरी को आठ बराबर भागों में बाँटते हैं। इसके सातवें भाग पर बिन्दु P अंकित करते हैं।

इस प्रकार संख्या रेखा पर बिन्दु P, \(\frac { 7 }{ 8 }\) को दर्शाता है।
![]()
(iii) हम जानते हैं कि \(\frac { -8 }{ 3 }\) या -2\(\frac { 2 }{ 3 }\),-3 से बड़ी तथा -2 से छेटी है। अत: भिन्न \(\frac { -8 }{ 3 }\), 2व – 3 के बीच में होगी।
अब हमें को दर्शाना है इसलिए हम 0 व 1,-1 व -2 तथा -2 व 3 की दूरी तीन बराबर भागों में बाँटते हैं। इसके शून्य से आठवें भाग पर बिन्दु P अंकित करते हैं।
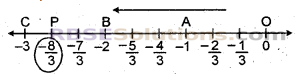
इस प्रकार संख्या रेखा पर बिन्दु P, \(\frac { -8 }{ 3 }\) को दर्शाता है।
(iv) हम जानते हैं कि -2\(\frac { 1 }{ 2 }\) या \(\frac { -5 }{ 2 }\),-3 से बड़ी व -2 से छोटी है।
अतः भिन् -2\(\frac { 1 }{ 2 }\), -2 व -3 को बीच में होगी।
अब हमें -2\(\frac { 1 }{ 2 }\) को दर्शाना(RBSESolutions.com)है, इसलिए हम 0 व – 1,-1 व -2 तथा -2 व -3 की दूरी दो बराबर भागों में बाँटते हैं।
इसके शून्य से पाँचवें भाग पर बिन्दु P अंकित करते हैं।

इस प्रकार, संख्या रेखा पर बिन्दु P, -2\(\frac { 1 }{ 2 }\) ( या –\(\frac { 5 }{ 2 }\)) को दर्शाता है।
![]()
(v) हम जानते हैं कि \(\frac { 5 }{ 7 }\) , शून्य से बड़ा और 1 से छोटा है।
∴ भिन्न \(\frac { 5 }{ 7 }\), 0 व 1 के बीच में होगी।
अब हमें \(\frac { 5 }{ 7 }\) को दर्शाना है, इसलिए हम 0 और 1 के बीच की दूरी को सात बराबर भागों में बाँटते हैं। इसके पाँचवे भाग पर बिन्दु P अंकित करते हैं।
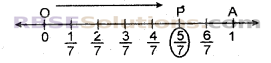
इस प्रकार संख्या रेखा पर बिन्दु P,\(\frac { 5 }{ 7 }\) को दर्शाता है।
![]()
प्रश्न 6
संकेतों >,< और = में से सही संकेत चुनकर रिक्त । स्थान भरिए।

हल:
(i) हम जानते हैं कि ऋणात्मक परिमेय संख्या,
धनात्मक परिमेय संख्या से छोटी होती है।
![]()
(ii) दी गई परिमेय संख्याओं(RBSESolutions.com)का हर 4 व 3 है और उनका ल.स. 12 है।

परिमेय संख्याओं की तुलना करने पर

![]()
(iii) दी गई परिमेय संख्याओं का हर 5 व 3 है और उनका ल.स. 15 है।
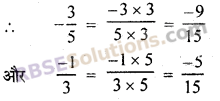
परिमेय संख्याओं की तुलना करने पर

(iv) दी गई परिमेय संख्याओं को हर 7 व 2 है और उनका ल.स. 14 है।

![]()
(v) दी गई परिमेय संख्याएँ
![]()
(vi) हम जानते हैं कि ऋणात्मक परिमेय संख्या, धनात्मक परिमेय संख्या से छोटी होती है। अतः
![]()
प्रश्न 7
निम्नलिखित परिमेय संख्याओं के बीच पाँच परिमेय संख्याएँ लिखिए

हल:
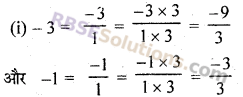
हम जानते हैं कि -9 और -3 के बीच पूर्णांक
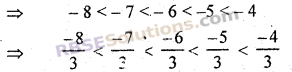
अतः -3 और -1 के बीच पाँच परिमेय संख्याएँ निम्न होगी
![]() आदि।
आदि।

हम जानते हैं कि 0 और 6 के(RBSESolutions.com)बीच पूर्णाक
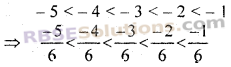
अत: 0 और -1 के बीच पाँच परिमेय संख्याएँ निम्न हैं
![]()

अब – 56 और – 50 के बीच पूर्णाक
– 55 < -54 < – 53 < -52 < -51
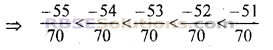
अत: \(\frac { -4 }{ 5 }\) और \(\frac { -5 }{ 7 }\) के बीच पाँच संख्याएँ निम्न हैं।
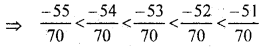 आदि।
आदि।
![]()
हम जानते हैं कि 12 और 6 के बीच पूर्णांक संख्याएँ
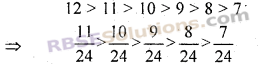
अतः \(\frac { 1 }{ 2 }\) और ,\(\frac { 1 }{ 4 }\) के बीच पाँच परिमेय संख्याएँ
![]()
(v) \(\frac { 2 }{ 5 }\) और \(\frac { -4 }{ 5 }\) के बीच पाँच परिमेय संख्याएँ
![]()
अतः \(\frac { 2 }{ 5 }\) और \(\frac { -4 }{ 5 }\) के बीच पाँच परिमेय संख्याएँ

– 10 और 0 के बीच पूर्णांक संख्याएँ
– 9< – 8 < -7 < – 6 < -5 ……… -1

![]()
प्रश्न 8
निम्नलिखित प्रत्येक प्रतिरूप(RBSESolutions.com)में तीन और परिमेय संख्याएँ लिखिए।

हल:

![]()
प्रश्न 9
निम्नलिखित परिमेय संख्याओं को आरोही क्रम में लिखिए।

![]()
हल:
(i) दी गई परिमेय संख्याओं में हर धनात्मक है।
2, 2, 4, 4 का ल.स. = 4
दी गई परिमेय(RBSESolutions.com)संख्याओं के हरों को 4 बनाने पर

दी गई परिमेय संख्याओं का हर धनात्मक है।

![]()
दी गई परिमेय संख्याओं का हर धनात्मक है।
∴ 11, 15, 1, 1; 15 का ल.स. = 165
दी गई परिमेय संख्याओं के हरों को 165 बनाने पर
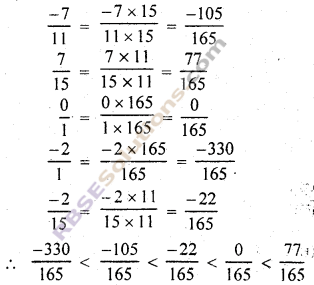
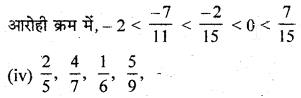
![]()
दी गई परिमेय संख्याओं का हर धनात्मक है।
∴ 5, 7, 6, 9 का ल.स. = 630
दी गई परिमेय(RBSESolutions.com)संख्याओं के हरों को 630 बनाने पर

![]()
प्रश्न 10
निम्नलिखित परिमेय संख्याओं को अवरोही क्रम में लिखिए

हल:
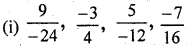
∴ 24, 4, 12, 16 का ल.स. = 48
दी गई परिमेय संख्याओं के हरों को 48 बनाने पर
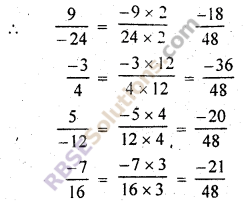

![]()
दी गई परिमेय संख्याओं का हर धनात्मक है।
∴ 6, 6, 9, 12 का ल.स. = 36
दी गई परिमेय(RBSESolutions.com)संख्याओं के हरों को 36 बनाने पर।

दी गई परिमेय संख्याओं के हरों को 6 बनाने पर
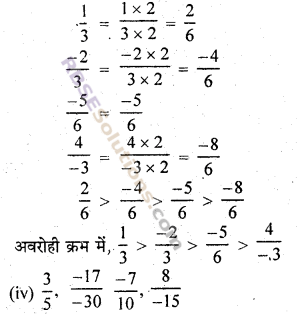
∴ 5, 30, 10, 15 का ल.स. = 30
दी गई परिमेय संख्याओं के हरों को 30 बनाने पर
![]()
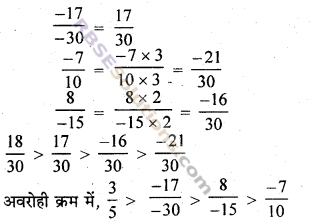
![]()
We hope the RBSE Solutions for Class 7 Maths Chapter 4 परिमेय संख्याएँ Ex 4.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 7 Maths Chapter 4 परिमेय संख्याएँ Exercise 4.1, drop a comment below and we will get back to you at the earliest.