RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ In Text Exercise

RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ In Text Exercise is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 1 परिमेय संख्याएँ In Text Exercise.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 8
Subject	Maths
Chapter	Chapter 1
Chapter Name	परिमेय संख्याएँ
Exercise	In Text Exercise
Number of Questions	27
Category	RBSE Solutions

Rajasthan Board RBSE Class 8 Maths Chapter 1 परिमेय संख्याएँ In Text Exercise

पृष्ठ 2
करो और सीखो

प्रश्न 1
मान ज्ञात कीजिए

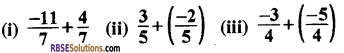
हल:

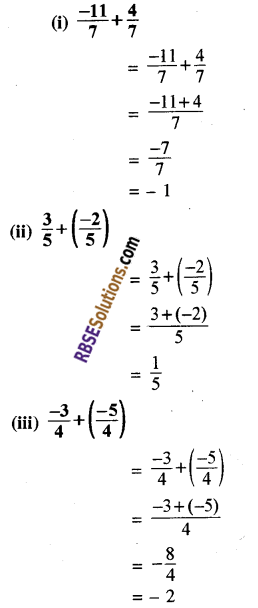
पृष्ठ 4
करो और सीखो

प्रश्न 2
मान ज्ञात कीजिए

हल:

5 और 6 का ल.स. 30 है।
हरों को समान करने पर

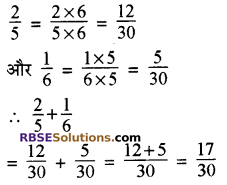
8 और 2 का ल.स. 8 है।
हरों को समान करने पर

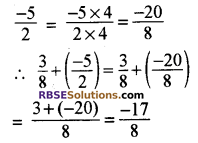
20 और 3 का ल.स. 60 है।
हरों को समान करने पर

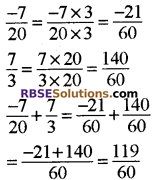
7 और 4 का ल.स. 28 है।
हरों को समान करने पर



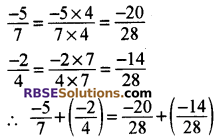
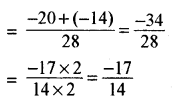
पृष्ठ 5
करो और सीखो

प्रश्न 1
मान ज्ञात कीजिए

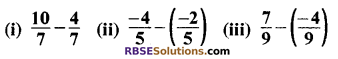
हल:

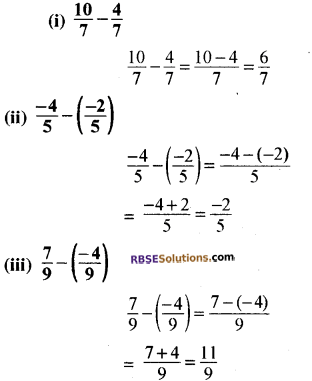
पृष्ठ 6
करो और सीखो

प्रश्न 1
मान ज्ञात कीजिए

हल:

3 और 8 का ल.स. 24 है।
हरों को समान करने पर

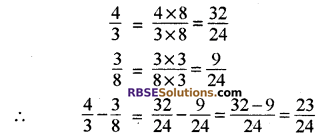
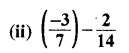
7 और 14 का ल.स. 14 है।
हरों को समान करने पर


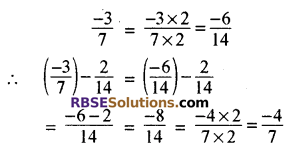
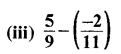
9 और 11 का ल.स. 99 है।
हरों को समान करने पर

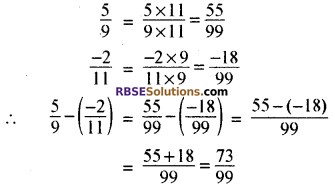
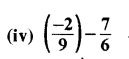
9 और 6 का ल.स. 18 है।
हरों को समान करने पर

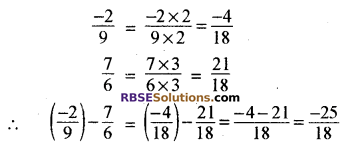
पृष्ठ 7
करो और सीखो
प्रश्न 1
मान ज्ञात कीजिए

हल:

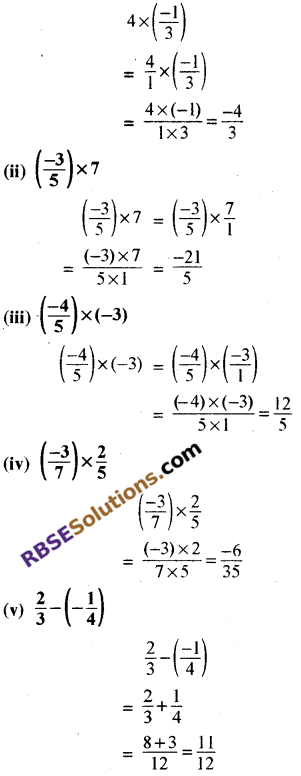
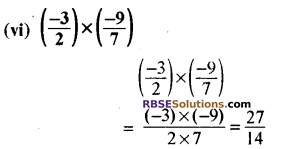
पृष्ठ 8
करो और सीखो

प्रश्न 1
हल कीजिए

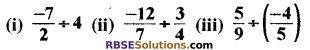
हल:

पृष्ठ 8
परिमेय संख्या में उसी परिमेय का भाग

प्रश्न 1
आप भी कुछ ऐसे ही अन्य उदाहरण देखिए।
हल:
कुछ ऐसे ही उदाहरण निम्न हैं

उदाहरण 1

उदाहरण 2

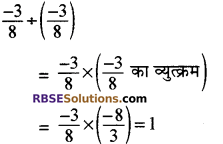
किसी परिमेय संख्या में उसी परिमेय संख्या से भाग करते हैं तो भागफल सदैव 1 प्राप्त होता है।
दूसरे शब्दों में, किसी परिमेय संख्या का(RBSESolutions.com) उसके व्युत्क्रम से गुणनफल सदैव 1 होता है।

पृष्ठ 9
करो और सीखो
प्रश्न 1
हल कीजिए

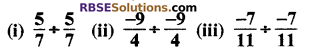
हल:

पृष्ठ 9
परिमेय संख्याओं के गुणधर्म
(i) योग-आइये, दो परिमेय संख्याओं के योग पर विचार करते हैं।
\(\frac { 3 }{ 5 }\) + \(\frac { 5 }{ 3 }\) = \(\frac { 9 }{ 12 }\) + \(\frac { 20 }{ 12 }\) = \(\frac { 9+20 }{ 12 }\) = \(\frac { 29 }{ 12 }\) एक परिमेय संख्या हैं।

प्रश्न 1
ऐसी ही कुछ और संख्याओं के साथ जाँच कीजिए।
हल:

नोट-किन्हीं दो परिमेय संख्याओं ४ तथा y के लिए (x +y) भी एक परिमेय संख्या है।

पृष्ठ 9
(ii) व्यवकलन-आइये, दो परिमेय संख्याओं के व्यवकलन पर विचार करते हैं।
\(\frac { 5 }{ 7 }\) – \(\frac { 3 }{ 8 }\) = \(\frac { 40 }{ 56 }\) – \(\frac { 21 }{ 56 }\) = \(\frac { 40-21 }{ 56 }\) = \(\frac { 19 }{ 56 }\) एक परिमेय संख्या है।
\(\frac { 1 }{ 4 }\) – \(\frac { 1 }{ 4 }\) = \(\frac { 1-1 }{ 4 }\) + \(\frac { 0 }{ 4 }\) = 0 एक परिमेय संख्या है।

प्रश्न 1
ऐसी ही कुछ और संख्याओं के साथ जाँच कीजिए।
हल:

नोट-किन्हीं दो परिमेय संख्याओं ॥ तथा y के लिए (x -y) भी एक परिमेय संख्या है।

पृष्ठ 10
(iii) गुणन – आइये, अब दो परिमेय संख्याओं के गुणनफल का अध्ययन करते हैं

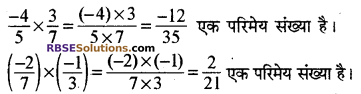
प्रश्न 1
ऐसी ही कुछ और संख्याओं के साथ जाँच कीजिए।
हल:

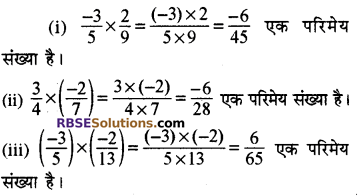
नोट-किन्हीं दो परिमेय संख्याओं x तथा y के लिए (xx y) भी एक परिमेय संख्या है।
(iv) भाग-आइये, अब दो परिमेय संख्याओं के भाग का अध्ययन करते हैं

अतः हम कह सकते हैं कि दो परिमेय संख्याओं का भाग सदैव एक परिमेय संख्या ही हो, यह आवश्यक नहीं है। (RBSESolutions.com) अतः परिमेय संख्यायें भाग के अन्तर्गत संवृत नहीं हैं।

करो और सीखो
सारणी में खाली स्थानों को भरिए

संख्याएँ	संक्रिया के अन्तर्गत संवृत हैं।
	योग	व्यवकलन	गुणन	भाग
प्राकृत संख्या	हाँ	……..	……..	……
पूर्ण संख्या	……	…….	………	नहीं
पूर्णांक	……..	हाँ	…….	…….
परिमेय संख्या	……..	…….	हाँ	…….

हल:

संख्याएँ	संक्रिया के अन्तर्गत संवृत हैं।
	योग	व्यवकलन	गुणन	भाग
प्राकृत संख्या	हाँ	नहीं	हाँ	नहीं
पूर्ण संख्या	हाँ	नहीं	हाँ	नहीं
पूर्णांक	हाँ	हाँ	हाँ	नहीं
परिमेय संख्या	हाँ	हाँ	हाँ	नहीं

पृष्ठ 11
क्रम विनिमेय गुणधर्म
(i) योग-दो परिमेय संख्याओं \(\frac { 3 }{ 7 }\),\(\frac { -1 }{ 7 }\) को जोड़कर देखिये

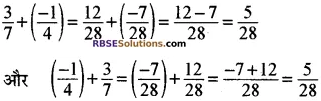
अतः परिमेय संख्याओं के लिए योग क्रम विनिमेय है, (RBSESolutions.com) अर्थात् किन्हीं परिमेय संख्याओं a और B के लिए।
a + b = b + a

प्रश्न 1
आप ऐसी ही कुछ और परिमेय संख्याएँ लेकर योग के लिए क्रम विनिमेय गुणधर्म की जाँच कीजिए।
हल:


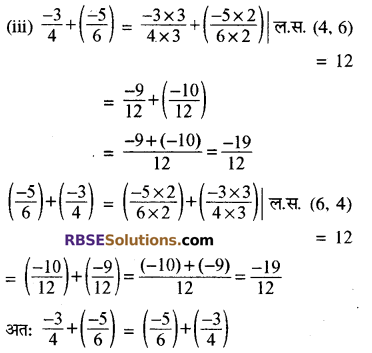
नोट-परिमेय संख्याओं के लिए योग क्रम विनिमेय हैं, अर्थात् किन्हीं परिमेय संख्याओं a और B के लिए
a + b = b + a

पृष्ठ 11
(ii) व्यवकलन-दो परिमेय संख्याओं है और न को घटाकर, देखिये।

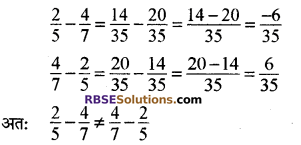
अतः परिमेय संख्याओं के लिए व्यवकलन क्रम विनिमेय नहीं है,(RBSESolutions.com)अर्थात् परिमेय संख्याओं a और B के लिए
a – b + b – a

पृष्ठ 12
(i) गुणन-दो परिमेय संख्याओं में और \(\frac { -4 }{ 5 }\) और \(\frac { 3 }{ 7 }\)का गुणा करके देखिये।

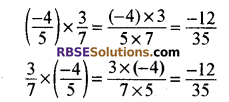
अतः यह आपस में बराबर है। इसलिए कहा जा सकता है। कि परिमेय संख्याओं के लिए गुणन क्रम विनिमेय है। अर्थात् किन्हीं परिमेय संख्याओं a और B के लिए
a x b = b x a

प्रश्न 1
आप ऐसी ही कुछ और परिमेय संख्याएँ लेकर गुणन के लिए क्रम विनिमेय गुणधर्म की जाँच कीजिए।
हल:

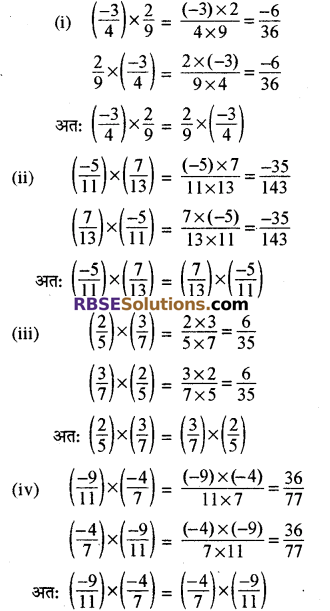
नोट-परिमेय संख्याओं के लिए गुणन क्रम विनिमेय हैं, अर्थात् किन्हीं परिमेय संख्याओं a और b के लिए।
a x b = b x a

(iv) भाग-परिमेय संख्याओं के लिए भाग क्रम विनिमेय नहीं है(RBSESolutions.com) अर्थात् किन्हीं परिमेय संख्याओं a और b के लिए
a ÷ b ≠ b ÷ a

करो और सीखो
सारणी में खाली स्थानों को भरिएसंख्याएँ

संख्याएँ	क्रम विनिमेयता
	योग	व्यवकलन	गुणन	भाग
प्राकृत संख्या	हाँ	नहीं	हाँ	नहीं
पूर्ण संख्या
पूर्णांक
परिमेय संख्या

हल:

संख्याएँ	क्रम विनिमेयता
	योग	व्यवकलन	गुणन	भाग
प्राकृत संख्या	हाँ	नहीं	हाँ	नहीं
पूर्ण संख्या	हाँ	नहीं	हाँ	नहीं
पूर्णांक	हाँ	नहीं	हाँ	नहीं
परिमेय संख्या	हाँ	नहीं	हाँ	नहीं

पृष्ठ 13
करो और सीखो
प्रश्न
क्या दोनों ओर के योग समान हैं?

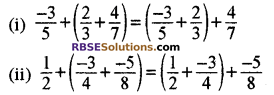
हल:

प्रश्न 1
ऐसे ही अन्य उदाहरण लेकर आप भी जाँच कीजिए कि क्या योगफल समान प्राप्त होता है?
हल:


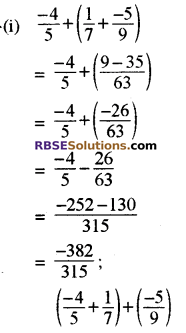
नोट – परिमेय संख्याओं के लिए योग साहचर्य है, अर्थात् किन्हीं तीन परिमेय संख्याओं a, b और c के लिए,
a + (b + c) = (a + b) + c

पृष्ठ 14
प्रश्न 1
कुछ और परिमेय संख्याएँ लेकर स्वयं गुणन साहचर्य नियम की जाँच कीजिए।
हल:



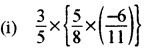
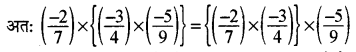
नोट-परिमेय संख्याओं के लिए गुणन साहचर्य है, अर्थात् किन्हीं तीन परिमेय संख्याओं a, b और c के लिए
a x (b x c) = (ax b) x c

पृष्ठ 15
करो और सीखो
सारणी में खाली स्थानों को भरिए

संख्याएँ	साहचर्य
	योग	व्यवकलन	गुणन	भाग
प्राकृत संख्या	हाँ	……	…..	…….
पूर्ण संख्या	……	……	……	नहीं
पूर्णांक	……	……	हाँ	……
परिमेय संख्या	……	……	……	……

हल:

संख्याएँ	साहचर्य
	योग	व्यवकलन	गुणन	भाग
प्राकृत संख्या	हाँ	नहीं	हाँ	नहीं
पूर्ण संख्या	हाँ	नहीं	हाँ	नहीं
पूर्णांक	हाँ	नहीं	हाँ	नहीं
परिमेय संख्या	हाँ	नहीं	हाँ	नहीं

पृष्ठ 16
प्रश्न 1
क्या प्राकृत संख्याओं में योज्य तत्समक है?
हल:
हाँ। योज्य तत्समक = 0

करो और सीखो
प्रश्न 1
रिक्त स्थानों की पूर्ति कीजिए

हल:

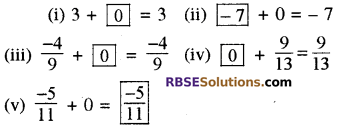
प्रश्न 2
रिक्त स्थानों की पूर्ति कीजिए


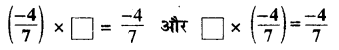
हल:

नोट-किसी भी परिमेय संख्या को 1 से गुणा करते हैं, तो गुणनफल वही परिमेय संख्या प्राप्त होती है। अर्थात् किसी परिमेय संख्या 4 के लिए
a x 1 = 1 x a = a

प्रश्न 3
सोचें! पूर्णाक और पूर्ण संख्याओं के लिए। गुणात्मक तत्समक क्या है?
हल:
पूर्णांक और पूर्ण संख्याओं के (RBSESolutions.com) लिए गुणात्मक तत्समक 1 है।

पृष्ठ 17
प्रश्न 1
रिक्त स्थानों की पूर्ति कीजिए

हल:

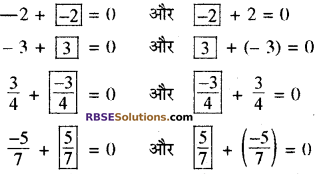
नोट – जब दो संख्याओं का योग शून्य (योज्य तत्समक) हो तो वे दोनों संख्यायें एक दूसरे की योज्य प्रतिलोम होती हैं।

करो और सीखो

प्रश्न 2
निम्न परिमेय संख्याओं के योज्य प्रतिलोम लिखिए

हल:

प्रश्न 3
रिक्त स्थानों की पूर्ति कीजिए

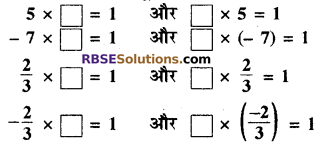
हल:

नोट –\(\frac { a }{ b }\) का गुणात्मक प्रतिलोम \(\frac { b }{ a }\) तथा \(\frac { b }{ a }\) का गुणात्मक प्रतिलोम \(\frac { a }{ b }\) है।

पृष्ठ 18
प्रश्न 1
क्या आप बता सकते हैं कि शून्य का गुणात्मक प्रतिलोम क्या है?
हल:
शून्य का गुणात्मक प्रतिलोम(RBSESolutions.com) अपरिभाषित होता है।

करो और सीखो
प्रश्न 2
परिमेय संख्या 3,\(\frac { 1 }{ 5 }\) ,\(\frac { -3 }{ 7 }\) ,\(\frac { 2 }{ 3 }\),\(\frac { -5 }{ 6 }\) के गुणात्मक प्रतिलोम लिखिए।
हल:
परिमेय संख्या 3 का गुणात्मक प्रतिलोम = \(\frac { 1 }{ 3 }\)
परिमेय संख्या \(\frac { 1 }{ 5 }\) का गुणात्मक प्रतिलोम =5
परिमेय संख्या \(\frac { -3 }{ 7 }\) का गुणात्मक प्रतिलोम = \(\frac { -7 }{ 3 }\)
परिमेय संख्या \(\frac { 2 }{ 3 }\) का गुणात्मक प्रतिलोम = \(\frac { 3 }{ 2 }\)
परिमेय संख्या \(\frac { -5 }{ 6 }\) का गुणात्मक प्रतिलोम = \(\frac { -6 }{ 5 }\)

प्रश्न 3
क्या परिमेय संख्याओं के लिए(RBSESolutions.com) व्यवकलन पर गुणन की वितरकता सत्य है?
हल:
हाँ ! परिमेय संख्याओं के लिए व्यवकलन पर गुणन की वितरकता सत्य है।

पृष्ठ 19
करो और सीखो

प्रश्न:
वितरण नियम (वितरकता) का उपयोग कर निम्नलिखित का मान ज्ञात कीजिए

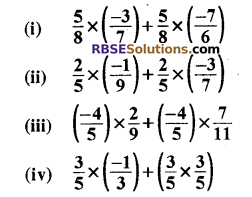
हल:

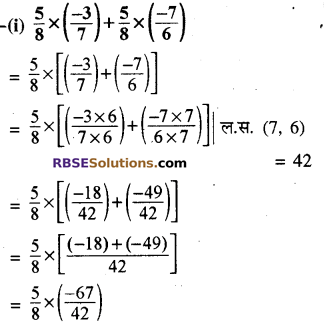
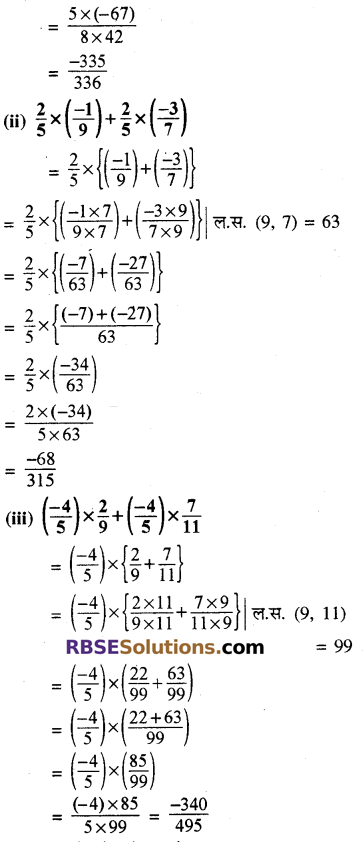
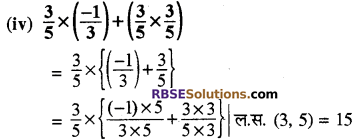
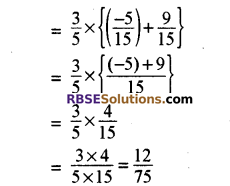
पृष्ठ 20
करो और सीखो

1.-1 और 2 के मध्य की परिमेय संख्या लिखिए।
2. \(\frac { 2 }{ 3 }\) और \(\frac { 3 }{ 4 }\) के मध्य की परिमेय संख्या लिखिए।
3. 2 और 3 के मध्य की तीन परिमेय (RBSESolutions.com) संख्याएँ लिखिए।
हल:

We hope the RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ In Text Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 1 परिमेय संख्याएँ In Text Exercise , drop a comment below and we will get back to you at the earliest.