RBSE Solutions for Class 8 Maths Chapter 11 एक चर राशि वाले रैखिक समीकरण Additional Questions

RBSE Solutions for Class 8 Maths Chapter 11 एक चर राशि वाले रैखिक समीकरण Additional Questions is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 11 एक चर राशि वाले रैखिक समीकरण Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	एक चर राशि वाले रैखिक समीकरण
Exercise	Additional Questions
Number of Questions	35
Category	RBSE Solutions

Rajasthan Board RBSE Class 8 Maths Chapter 11 एक चर राशि वाले रैखिक समीकरण Additional Questions

I. बहुविकल्पात्मक प्रश्न

1. रैखिक समीकरण की आवश्यक शर्त है –
(a) चर की अधिकतम घात 1 होना
(b) चर की अधिकतम घात 2 होना
(c) चर की(RBSESolutions.com)अधिकतम घात 3 होना
(d) इनमें से कोई नहीं

2. पक्षान्तरण करते समय ‘+’ का चिह्न बदलता है –
(a) ‘x’ में
(b) ‘÷’ में
(c) ‘-‘ में
(d) वही रहता है।

3. 3x = 21 में x का मान होगा –
(a) 7
(b) 24
(c) 18
(d) 63

4. रैखिक समीकरण का हल हो सकती है –
(a) कोई भी प्राकृत संख्या
(b) कोई भी परिमेय संख्या
(c) कोई भी(RBSESolutions.com)वास्तविक संख्या
(d) कोई भी पूर्ण संख्या

5. 3 – 4 = 5 का हल होगा –
(a) 4 x 5
(b) 5 x 4
(c) 5 – 4
(d) 5 + 4

6. निम्नलिखित में से रैखिक समीकरण है –

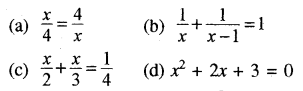
7. समीकरण (x – 1)² = x² – 3 की घात है –
(a) 1
(b) 2
(c) 0
(d) 3

8. समीकरण = \(\frac { 5 }{ x }\) 2 का हल है –
(a) 10
(b) \(\frac { 2 }{ 5 }\)
(c) \(\frac { 5 }{ 2 }\)
(d) \(\frac { 1 }{ 10 }\)

उत्तरमाला:
1. (a) 2. (c) 3. (a) 4. (c) 5. (d) 6. (c) 7. (a) 8. (c).

II. रिक्त स्थानों की पूर्ति कीजिए

1. समीकरणों में सदैव …………… का चिह्न प्रयुक्त होता है।
2. संख्याओं की भाँति चरों को भी एक पक्ष से दूसरे पक्ष में ……………… किया जा सकता है।
3. समीकरण के दोनों(RBSESolutions.com)पक्षों पर एक जैसी ही गणितीय संक्रियाएँ करते हैं जिससे समीकरण का ……………. बना रहता है।
4. रैखिक समीकरणों की उपयोगिता उनके विविध ……………. में है।
5. यदि x एक विषम संख्या है तो इससे पूर्व की सबसे बड़ी विषम संख्या ……………. होगी।

उत्तरमाला:
1. ‘=’ 2. पक्षान्तरित 3. सन्तुलन 4. अनुप्रयोगों 5. x – 2

III. सत्य/असत्य

1. z ÷ 4 = – 8 का मूल 32 है।
2. 3x = \(\frac { 20 }{ 7 }\) – x का मूल \(\frac { 5 }{ 7 }\) है।
3. समीकरण 2x + 3 = 2(x – 4) का मूल विद्यमान नहीं है।
4. तीन क्रमागत संख्याओं में सबसे(RBSESolutions.com)बड़ी संख्या x + 1 है। सबसे छोटी संख्या x होगी।

उत्तरमाला:
1. असत्य 2. सत्य 3. सत्य 4. असत्य।

IV. मिलान/सुमेलन वाले प्रश्न

उत्तरमाला:
1. ↔ (c)
2. ↔ (d)
3. ↔ (a)
4. ↔ (b)

V. अतिलघूत्तरात्मक प्रश्न

प्रश्न 1
बीजीय समीकरणों में LHS से क्या आशय है?
उत्तर:
बीजीय समीकरणों में LHS से आशय समता के बाईं ओर वाले व्यंजक से है।

प्रश्न 2
रैखिक समीकरणों के उपयोग से कौनसी समस्याएँ हल की जा सकती हैं?
उत्तर:
रैखिक समीकरणों के उपयोग(RBSESolutions.com)से संख्याओं, आयु, परिमापों तथा मुद्रा के रूप में प्रयोग होने वाले सिक्कों व नोटों पर आधारित अनेक प्रकार की समस्याएँ हल की जा सकती हैं।

प्रश्न 3
2 – 3 = 7 का हल ज्ञात कीजिए।
हल:
2x – 3 = 7
⇒ 2x= 7 + 3
⇒ 2x = 10
⇒ x = \(\frac { 10 }{ 2 }\) = 5

प्रश्न 4
हल कीजिए – 2x – 3 = x + 2
हल:
2x – 3 = x + 2
2x – x = 2 + 3
= 5

VI. लघूत्तरात्मक प्रश्न

प्रश्न 1
समीकरण 4r -[2 + {x – (3 – x)}] = 3x +6 को हल कीजिए।
हल:
4 – [2 + {x – (3 – x)}] = 3x + 6
⇒ 4x – 12 + (x – 3+ x] = 3x+6
⇒ 4x – [2 + 2x – 3] = 3x+6
⇒ 4x – (2 – 1) = 3x+6
⇒ 4x – 2x +1 = 3x +6
⇒ 2x +1 = 3x +6
⇒ 2x – 3x = 6 – 1
⇒ -x = 5
⇒ x = -5

प्रश्न 2
समीकरण √3x – 2 = 2√3 + 4 का हल ज्ञात कीजिए।
हल:
√3x – 2 = 2√3 + 4
⇒ √3x = 2 + 2√3 + 4
⇒ √3x = 2√3 + 6
⇒ √3x = 2√3(1+√3)
⇒ x = \(\frac { 2\sqrt { 3 } (1+\sqrt { 3 } ) }{ \sqrt { 3 } }\)
⇒ x= 2(1+√3)

प्रश्न 3.
समीकरण \(\frac { 8x + 3 }{ 2x – 4 }\) = \(\frac { 4x}{ x – 5 }\) +9 को हल कीजिए।
हल:
⇒ (8x + 3) (x – 5) = 4x (2x – x)
⇒ 8x – 40x + 3x – 15 = 8x² – 16x
⇒ – 40x + 3x + 16x = 15
⇒ – 21x = 15
⇒ x = \(\frac { -15 }{ 21 }\)
⇒ x = \(\frac { -5 }{ 7 }\)

प्रश्न 4
एक थैली में 2 रुपये व 5 रुपये के कुल 15 सिक्के रखे हुए हैं। सिक्कों का कुल मूल्य 45 रुपये हो तो प्रत्येक प्रकार के सिक्कों की संख्या ज्ञात कीजिए।
हल:
माना 2 रुपये के सिक्कों की संख्या x है।
तब 5 रुपये के सिक्कों की संख्या = 15 – x
2 रुपये के(RBSESolutions.com)सिक्कों का मूल्य = 2 रुपये
5 रुपये के सिक्कों का मूल्य = 5 (15 – x) रुपये
प्रश्न की शर्त के अनुसार
⇒ 2x + 5 (15 – x) = 45
⇒ 2x + 75 – 5x = 45
⇒ 2x – 5x + 75 = 45
⇒ -3x + 75 = 45
⇒ -3x = 45 – 75
⇒ -3x = -30
⇒ x = \(\frac { -30 }{ -3 }\)
⇒ x = 10
अतः 2 रुपये के सिक्कों की संख्या = 10
तथा 5 रुपये के सिक्कों की संख्या = 15 – 10 = 5

प्रश्न 5. तीन क्रमागत संख्याएँ ज्ञात कीजिए जहाँ पहली संख्या का दुगुना, दूसरी संख्या का तिगुना तथा तीसरी संख्या का चौगुना मिलकर 182 के बराबर होते हैं।
हल:
माना तीन क्रमागत संख्याएँ x,x+1 और x + 2 हैं।
तब प्रश्न की शर्त के अनुसार
2x + 3(x + 1) + 4 (x + 2) = 182
⇒ 2x + 3x + 3 + 4x + 8 = 182
⇒ 9x + 11 = 182
⇒ 9x = 182 – 11
⇒ 9x = 171
⇒ x = \(\frac { 171 }{ 9 }\) = 19
अतः पहली संख्या = 19
दूसरी(RBSESolutions.com)संख्या = 19 + 1 = 20
तथा तीसरी संख्या = 19 + 2 = 21

प्रश्न 6
रमेश के पिता की आयु रमेश से 27 वर्ष अधिक है। 5 वर्ष बाद रमेश की आयु और उसके पिता की आयु का अनुपात 2 : 3 हो जायेगा। दोनों की। वर्तमान आयु बताओ।
हल:
माना कि रमेश की आयु = x वर्ष
तो पिता की आयु = (x + 27) वर्ष
5 वर्ष बाद रमेश की आयु = (x + 5) वर्ष
5 वर्ष बाद पिता की आयु = x + 27 + 5
= (x + 32) वर्ष
प्रश्नानुसार, \(\frac { x+5 }{ x+32 }\) = \(\frac { 2 }{ 3 }\)
या 3(x + 5) = 2(x + 32)
या 3x + 15 = 2x + 64
या 3x – 2x = 64 – 15
या x = 49
रमेश की आयु = 49 वर्ष
पिता की(RBSESolutions.com)आयु x + 27 = 49 + 27 = 76 वर्ष

प्रश्न 7
हल कीजिए

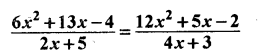
हल:

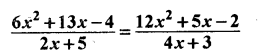
(6x² + 13 – 4) (4x + 3) = (12x² + 5x – 2) (2x + 5) (वज्र गुणन से)
⇒ (6x² + 13x – 4) x 4x + (6x² + 13x -4) x 3
⇒ (12x² +5x – 2) x 2x + (12x² + 5x – 2) x 5
⇒ 24x³ + 52x² – 16x + 18x² + 39x – 12 = 24x³ + 10x² – 4x + 60x² + 25x – 10
⇒ 24x³ + 70x² + 23x – 12 = 24x³ + 70x² + 21x – 10
⇒ 24x³ + 70x² + 23x – 24x³ – 70² – 21x = – 10 + 12
⇒ 2x = 12
⇒ x = 1
अतः x = 1, दिए गए समीकरण का अभीष्ट हल है।

प्रश्न 8
एक परिमेय संख्या का हर उसके अंश से 5 अधिक है। यदि अंश तथा हर में 2 जोड़ दिया जाए तो \(\frac { 1 }{ 2 }\) हमें प्राप्त होता है। परिमेय संख्या ज्ञात कीजिए।
हल:
माना परिमेय संख्या का अंश x है। प्रश्नानुसार हर का मान उसके अंश से 5 अधिक है। अतः परिमेय संख्या होगी = \(\frac { x }{ x+5 }\)
अब अंश और हर में दो, दो जोड़ने पर
\(\frac { x+2 }{ x+5+2 }\) = \(\frac { 1 }{ 2 }\)
⇒ 2(x + 2) = x +7
⇒ 2x + 4 = x + 7
⇒ 2x – x = 7 – 4
⇒ x = 3
अतः अंश = 3
हर = 3 + 5 = 8
अभीष्ट(RBSESolutions.com)’परिमेय संख्या = \(\frac { 3 }{ 8 }\)

प्रश्न 9
एक आयत की लम्बाई, चौड़ाई से 3 मीटर अधिक है। यदि उसका परिमाप 54 मीटर है तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल:
माना आयत की चौड़ाई = x मीटर
अतः आयत की लम्बाई = 3 + x मीटर
∵ परिमाप = 2 (ल. + चौ.)
अतः परिमाप = 2{(3 + x) + x}
= 2(2x + 3) मीटर
प्रश्नानुसार 2(2x + 3) = 54
अतः 2x + 3 = \(\frac { 54 }{ 2 }\)
2x + 3 = 27
2x = 27 – 3 = 24
x = \(\frac { 24 }{ 2 }\) = 12
अतः आयत की चौड़ाई = 12 मीटर
तथा आयत(RBSESolutions.com)की लम्बाई = 12 + 3 = 15 मीटर

प्रश्न 10
यदि 11 के तीन लगातार गुणजों का योग 363 है, तो उन्हें ज्ञात कीजिए।
हल:
माना 11 के तीन लगातार गुणज संख्याएँ 11x, 11(x + 1), 11(x + 2) हैं।
प्रश्नानुसार
11x + 11(x + 1) + 11(x + 2) = 363
⇒ 11x + 11x + 11 + 1lx + 22 = 363
⇒ 33x = 363 – 33
⇒ 33x = 330
⇒ x = \(\frac { 330 }{ 30 }\)
⇒ x = 10
तीन लगातार गुणज संख्याएँ
11x = 11 x 10 = 110
11(x + 1) = 11(10 + 1) = 11 X 11 = 121
11(x + 2) = 11(10 + 2) = 11 x 12 = 132
अतः तीन लगातार(RBSESolutions.com)गुणज संख्याएँ 110, 121, 132 हैं।

We hope the RBSE Solutions for Class 8 Maths Chapter 11 एक चर राशि वाले रैखिक समीकरण Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 11 एक चर राशि वाले रैखिक समीकरण Additional Questions, drop a comment below and we will get back to you at the earliest.