RBSE Solutions for Class 8 Maths Chapter 14 क्षेत्रफल Additional Questions is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 14 क्षेत्रफल Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | क्षेत्रफल |
| Exercise | Additional Questions |
| Number of Questions | 34 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 14 क्षेत्रफल Additional Questions
I. बहुविकल्पात्मक प्रश्न
प्रश्न 1
एक समकोण त्रिभुज का क्षेत्रफल 36 वर्ग सेमी. है। एवं आधार 9 सेमी. है तो लम्ब की लम्बाई होगी
(a) 8 सेमी.
(b) 4 सेमी.
(c) 16 सेमी.
(d) 32 सेमी.
प्रश्न 2
किसी समलम्ब चतुर्भुज(RBSESolutions.com) की समान्तर भुजाएँ 32 मी. और 20 मी. हैं तथा इनके मध्य दूरी 15 मी. है तो समलम्ब चतुर्भुज का क्षेत्रफल होगा
(a) 290 वर्ग मीटर
(b) 390 वर्ग मीटर
(c) 390 वर्ग मीटर
(d) 400 वर्ग मीटर
प्रश्न 3
एक समचतुर्भुज के विकर्ण 10 सेमी. एवं 8 सेमी. हों तो इसका क्षेत्रफल होगा
(a) 80 वर्ग सेमी.
(b) 40 वर्ग सेमी.
(c) 9 वर्ग सेमी.
(d) 36 वर्ग सेमी.
![]()
प्रश्न 4
किसी समलम्ब चतुर्भुज(RBSESolutions.com) का क्षेत्रफल 143 सेमी. है। उसकी समान्तर भुजाएँ क्रमशः 15 सेमी. व 11 सेमी. हैं। समान्तर भुजाओं के मध्य लम्बवत् दूरी है
(a) 11 सेमी.
(b) 15 सेमी.
(c) 13 सेमी.
(d) 14 सेमी.
प्रश्न 5
एक त्रिभुजाकार भूखण्ड का क्षेत्रफल 2.5 एअर है। यदि भूखण्ड का आधार 100 मीटर हो तो उसकी ऊँचाई है
(a) 10 सेमी.
(b) 5 सेमी.
(c) 10 मीटर
(d) 5 मीटर
प्रश्न 6
एक त्रिभुज और आयत एक(RBSESolutions.com) ही आधार व एक ही समान्तर रेखाओं के मध्य स्थित हैं। त्रिभुज का आधार 9 सेमी. व ऊँचाई 6 सेमी. है। आयत का क्षेत्रफल है
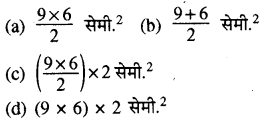
उत्तरमाला:
1. (a) 2. (b) 3. (b) 4. (a) 5. (d) 6. (c)
![]()
II. रिक्त स्थानों की पूर्ति कीजिए
1. त्रिभुज का क्षेत्रफल = ……… x आधार x ऊँचाई
2. समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x समान्तर भुजाओं का योग x ………
3. समचतुर्भुज(RBSESolutions.com) के विकर्ण परस्पर ………. होते हैं।
4. समचतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 4 }\) x …………… होता है। |
5. आयत का क्षेत्रफल = लम्बाई x ……….
उत्तरमाला:
1. \(\frac { 1 }{ 2 }\),
2. ऊँचाई,
3. लम्बवत्,
4. विकर्णो का गुणनफल,
5. चौड़ाई।
![]()
III. सत्य/असत्य
1, समान्तर चतुर्भुज, जिसका आधार 6.5 सेमी. और ऊँचाई 4 सेमी. है, 26 सेमी.2 होता है।
2. 1 आर = 100 वर्गमीटर होता है।
3. 1 हैक्टेयर = 10000 वर्गमीटर(RBSESolutions.com) होता है।
4. किसी समचतुर्भुज के विकर्ण 24 सेमी. व 7 सेमी. हैं, तो समचतुर्भुज का क्षेत्रफल 168 सेमी.2 होगा।
उत्तरमाला:
1, सत्य
2. सत्य
3. सत्य
4. असत्य
IV. मिलान/सुमेलन वाले प्रश्नखण्ड

उत्तरमाला:
1. ↔ (b)
2. ↔ (a)
3. ↔ (d)
4. ↔ (c)
![]()
V. अतिलघूत्तरात्मक प्रश्न
प्रश्न 1
समान्तर चतुर्भुज ABCD में AB = 35 सेमी. तथा इससे सम्बन्धित ऊँचाई 12 सेमी. है। समान्तर चतुर्भुज की भुजा BC = 25 सेमी. है, तो इस भुजा से सम्बन्धित ऊँचाई ज्ञात कीजिए।
हल:
समान्तर चतुर्भुज ABCD का क्षेत्रफल 35 x 12 = 25 x भुजा BC से सम्बन्धित ऊँचाई
⇒ भुजा BC से सम्बन्धित(RBSESolutions.com) ऊँचाई = \(\frac { 35\times 12 }{ 25 }\)
= 16.8 सेमी.
प्रश्न 2
निम्न चित्र में एक खेत ABCD समलम्ब चतुर्भुज के आकार का है। AB ॥ DC, DC = 25 सेमी., CE = 12 सेमी. तथा EB = 10 सेमी. है। चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
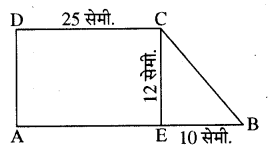
हल:
समलम्ब चतुर्भुज ABCD का क्षेत्रफल = आयत AECD का क्षेत्रफल + समकोण त्रिभुज CEB का क्षेत्रफल
= 25 x 12 + \(\frac { 10\times 12 }{ 2 }\)
= 300 + 60
= 360 वर्ग सेमी.
![]()
प्रश्न 3
एक समचतुर्भुज का(RBSESolutions.com) परिमाप 52 सेमी. है। उसकी दो समान्तर भुजाओं के मध्य लम्बवत् दूरी 12 सेमी. है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल:
समचतुर्भुज का परिमाप = 52 सेमी.
∴ समचतुर्भुज की एक भुजा = \(\frac { 52 }{ 4 }\) सेमी. = 13 सेमी.
समचतुर्भुज की ऊँचाई = 12 सेमी.
∴ समचतुर्भुज का क्षेत्रफल
= आधार x ऊँचाई
= 13 x 12
= 156 वर्ग सेमी.
![]()
VI. लघूत्तरात्मक प्रश्न
प्रश्न 1
समलम्ब चतुर्भुज का क्षेत्रफल 140 सेमी.2 है। इसकी ऊँचाई 10 सेमी. है। समान्तर भुजाओं का अन्तर 4 सेमी. है। दोनों समान्तर भुजाओं की लम्बाइयाँ ज्ञात कीजिए।
हल:
माना समान्तर(RBSESolutions.com) भुजाओं की लम्बाइयाँ a सेमी. और b सेमी. हैं जहाँ a> b.
समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x (समान्तर भुजाओं का योग) x ऊँचाई
⇒ 140 = \(\frac { 1 }{ 2 }\) (a + b) 10
⇒ 140 x 2 = (a + b) 10
⇒ 280 = (a + b) 10
⇒ a + b = \(\frac { 280 }{ 10 }\)
⇒ a + b = 28 ……….(1)
साथ ही a – b = 4 ………… (2)
(1) व (2) को जोड़ने पर
2a = 32
⇒ a = \(\frac { 32 }{ 2 }\) = = 16 सेमी.
(1) में a = 16 रखने पर
16 + b = 28
⇒ b = 28 – 16
⇒ b = 12 सेमी.
अतः समान्तर(RBSESolutions.com) भुजाओं की लम्बाइयाँ 16 सेमी. और 12 सेमी. हैं।
![]()
प्रश्न 2
एक समलम्ब चतुर्भुज की दो समान्तर भुजाएँ क्रमशः 12 सेमी. और 8 सेमी. हैं। यदि उसका क्षेत्रफल 60 वर्ग सेमी. हो तो समलम्ब चतुर्भुज की ऊँचाई ज्ञात कीजिए।
हल:
माना समलम्ब चतुर्भुज की ऊँचाई = h सेमी.
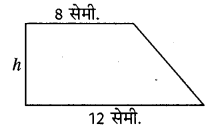
सूत्रानुसार,
समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\)(समान्तर भुजाओं का योग) x ऊँचाई
या 60 = \(\frac { 1 }{ 2 }\) x (12 + 8) x h
या h = \(\frac { 60\times 2 }{ 20 }\) = 6 सेमी.
अतः ऊँचाई = 6 सेमी.
प्रश्न 3
दिये गये(RBSESolutions.com) चित्र में ABCD एक समलम्ब चतुर्भुज है जिसमें AB | DC तथा DA 1 AB है। यदि AB = 13 cm., AD = 8 cm. तथा CD = 7 cm. है, तो समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
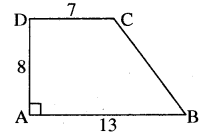
हल:
समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x (समान्तर भुजाओं का योग) x समान्तर भुजाओं के बीच की दूरी
= \(\frac { 1 }{ 2 }\) x (7 + 13) x 8
= \(\frac { 1 }{ 2 }\) x 20 x 8 = 80 वर्ग सेमी.
![]()
प्रश्न 4
बहुभुज ABCDE को विभिन्न भागों में बाँटा गया है जैसा कि आकृति में दर्शाया गया है। यदि AD = 8 सेमी., AH = 6 सेमी., AG = 4 सेमी., AF =3 सेमी. और BF = 2 सेमी., CH = 3 सेमी., EG = 2.5 सेमी. तो इसका क्षेत्रफल ज्ञात कीजिए।
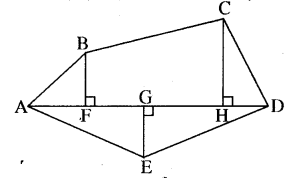
हल:
बहुभुज ABCDE का क्षेत्रफल = समकोण ∆AFB का क्षेत्रफल + समलम्ब चतुर्भुज BFHC का क्षेत्रफल + समकोण ∆CHD का क्षेत्रफल + समकोण ∆EGD का(RBSESolutions.com) क्षेत्रफल + समकोण ∆AGE का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x AF x BF + \(\frac { 1 }{ 2 }\) x (BF + CH) x FH + \(\frac { 1 }{ 2 }\) x HD x CH+ \(\frac { 1 }{ 2 }\) x GD x GE+ \(\frac { 1 }{ 2 }\) x AG x GE
=\(\frac { 1 }{ 2 }\) x 3 x 2 + \(\frac { 1 }{ 2 }\) x (2 + 3) x (6 – 3) + \(\frac { 1 }{ 2 }\) x (8 – 6) x 3 + \(\frac { 1 }{ 2 }\) x (8 – 4) x 2.5 +
FH = AH – AF = 6 – 3 = 3 सेमी.
HD = AD – AH = 8 – 6 = 2 सेमी.
GD = AD – AG = 8 – 4 = 4 सेमी.
= 3 + 7.5 + 3 + 5 +5
= 23.5 सेमी.2
![]()
प्रश्न 5
MP = 9 सेमी., MD = 7 सेमी., MC = 6 सेमी., MB = 4 सेमी., MA = 2 सेमी. तो बहुभुज MNOPQR का क्षेत्रफल ज्ञात कीजिए। NA, 0C, QD एवं RB विकर्ण MP(RBSESolutions.com) पर खींचे गये लम्ब हैं।
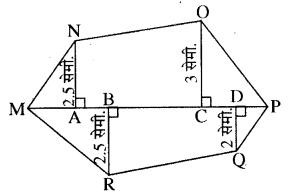
हल:
बहुभुज MNOPQR का क्षेत्रफल = ∆MAN का क्षेत्रफल + समलम्ब चतुर्भुज A∆CON का क्षेत्रफल + ∆OCP का क्षेत्रफल + ∆QDP को क्षेत्रफल + समलम्ब चतुर्भुज DBRQ का क्षेत्रफल + ∆RBM का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x AM x NA + \(\frac { 1 }{ 2 }\) x (NA + OC) x AC + \(\frac { 1 }{ 2 }\) x CP x OC + \(\frac { 1 }{ 2 }\) x DP X QD + \(\frac { 1 }{ 2 }\) x (BR + DQ) BD + \(\frac { 1 }{ 2 }\) x MB x BR
= \(\frac { 1 }{ 2 }\) x 2 x 2.5 + \(\frac { 1 }{ 2 }\) x (2.5 + 3) x 4 + \(\frac { 1 }{ 2 }\) x 3x 3 + \(\frac { 1 }{ 2 }\) x 2 x 2 + \(\frac { 1 }{ 2 }\) x (2.5 + 2) x 3 + 1 x 4 x 2.5
AC = MC – MA = 6 – 2 = 4 सेमी.
CP = MP – MC = 9 – 6 = 3 सेमी.
PD = MP – MD = 9 – 7 = 2 सेमी.
BD = MD – MB = 7 – 4 = 3 सेमी.
= 2.5 + 11 + 4.5 + 2 + 6.75 + 5
= 31.75 सेमी.
![]()
प्रश्न 6
एक नहर का अनुप्रस्थ काट समलम्ब चतुर्भुजाकार है। नहर ऊपर से 10 मीटर चौड़ी हो एवं पैंदे से 6 मीटर चौड़ी हो एवं अनुप्रस्थ काट को क्षेत्रफल 72 वर्ग मीटर(RBSESolutions.com) हो, तो इसकी गहराई ज्ञात कीजिए।
हल:
समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x (समान्तर भुजाओं का योग) x ऊँचाई = 72
⇒ \(\frac { 1 }{ 2 }\) x (10 + 6) x ऊँचाई
⇒ 72 = 8 x ऊँचाई
⇒ ऊँचाई = 72 = 9 मीटर
अतः गहराई 9 मीटर है।
प्रश्न 7
एक समचतुर्भुज के विकर्ण 15 सेमी. एवं 36 सेमी. हैं। इसका परिमाप एवं क्षेत्रफल ज्ञात कीजिए।
हल:
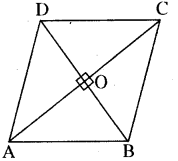
समचतुर्भुज का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x विकर्णो का गुणनफल
= \(\frac { 1 }{ 2 }\) x 15 x 36
= 270 वर्ग सेमी.
हम जानते हैं कि समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं।

= 19.5 सेमी.
∴ समचतुर्भुज का परिमाप = 4 x AB
= 4 x 19.5
= 78 सेमी.
![]()
प्रश्न 8
एक खेत जिसका आकार चित्र में दर्शाये गये बहुभुज ABCDEF के समान है। चित्र में दी गई सभी माप मीटर में हैं। बहुभुज ABCDEF का क्षेत्रफल ज्ञात कीजिए।
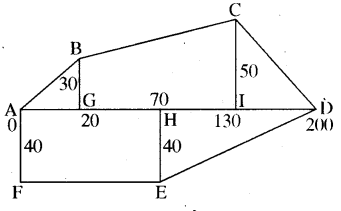
हल:
बहुभुज ABCDEF का क्षेत्रफल = आकृति ① का क्षेत्रफल + आकृति ② का क्षेत्रफल + आकृति ③ का क्षेत्रफल + आकृति ④ का क्षेत्रफल + आकृति ⑤ का क्षेत्रफल
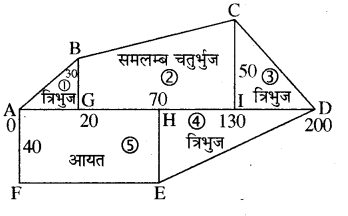
= \(\frac { 1 }{ 2 }\) x 20 x 30 + \(\frac { 1 }{ 2 }\) x (30 + 50) x (130 – 20) + \(\frac { 1 }{ 2 }\) x (200 – 130) x 50 + \(\frac { 1 }{ 2 }\) x (200 – 70) x 40 + 70 x 40
= 300 + 4400 + 1750 + 2600 + 2800
= 11850 वर्ग मीटर
![]()
प्रश्न 9
दिए गए खेत का क्षेत्रफल ज्ञात कीजिए। सभी माप मीटर में हैं।
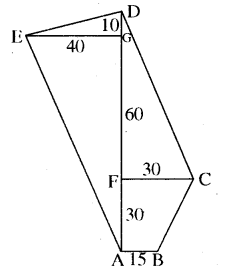
हल:
बहुभुज ABCDEA का क्षेत्रफल = ∆ADE का क्षेत्रफल + ∆DEC का क्षेत्रफल + समलम्ब चतुर्भुज ABCF का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x AD x EG + \(\frac { 1 }{ 2 }\) x DF x FC + \(\frac { 1 }{ 2 }\) x (AB + FC) x AF
= \(\frac { 1 }{ 2 }\) x 90 x 40 + \(\frac { 1 }{ 2 }\) x 60 x 30 + \(\frac { 1 }{ 2 }\) x (15 + 30) x 30
= 45 x 40 + 30 X 30 + 45 x 15
= 1800 + 900 + 675 = 3375 मीटर
![]()
प्रश्न 10
एक समचतुर्भुज ABCD का क्षेत्रफल 264 वर्ग सेमी. है। यदि इसका एक विकर्ण AC = 24 सेमी. है तो विकर्ण BD की माप बताइए।
हल:
हम जानते हैं कि
समचतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x विकर्णो का गुणनफल दिया है – समचतुर्भुज का क्षेत्रफल = 264 वर्ग सेमी, विकर्ण AC = 24 सेमी
ज्ञात करना है-विकर्ण BD
264 = \(\frac { 1 }{ 2 }\) x 24 x BD
BD = \(\frac { 264\times 2 }{ 24 }\) = 22 सेमी.
प्रश्न 11
एक समचतुर्भुज का क्षेत्रफल 360 वर्ग सेमी. है एवं विकर्षों में से एक विकर्ण की लम्बाई 20 सेमी. है, तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हल:
समचतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x विकर्णो का गुणनफल
⇒ 360 वर्ग सेमी. = \(\frac { 1 }{ 2 }\) x 20 सेमी. x दूसरा विकर्ण
⇒ दूसरा विकर्ण = \(\frac { 360\times 2 }{ 20 }\) सेमी. = 18 x 2 सेमी.
⇒ दूसरा विकर्ण = 36 सेमी.
![]()
प्रश्न 12
दी गई आकृति का(RBSESolutions.com) क्षेत्रफल ज्ञात कीजिए। (सभी माप मीटर में हैं।)
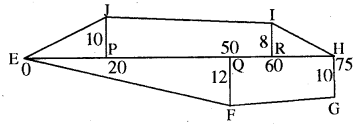
हल:
आकृति का कुल क्षेत्रफल = ∆PEJ का क्षेत्रफल + समलम्ब चतुर्भुज PRIJ का क्षेत्रफल + ∆IRH का क्षेत्रफल + समलम्ब चतुर्भुज HGFQ का क्षेत्रफल + ∆QFE का क्षेत्रफल
∆PEJ का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x ऊँचाई
= \(\frac { 1 }{ 2 }\) x 10 x 20
= 100 मीटर2
समलम्ब चतुर्भुज JPRI का क्षेत्रफल,
= \(\frac { 1 }{ 2 }\) (समान्तर भुजाओं का योग) x बीच की दूरी
= \(\frac { 1 }{ 2 }\) (10 + 8) x (60 – 20)
= \(\frac { 1 }{ 2 }\) x 18 x 40 = 360 मीटर2
∆IRH का(RBSESolutions.com) क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x ऊँचाई
= \(\frac { 1 }{ 2 }\) x 8 x (75 – 60)
= \(\frac { 1 }{ 2 }\) x 8 x 15 = 60 मीटर2
समलम्ब चतुर्भुज FGHQ का क्षेत्रफल = \(\frac { 1 }{ 2 }\) (समान्तर भुजाओं का योग) x बीच की दूरी
= \(\frac { 1 }{ 2 }\) x (10 + 12) x (75 – 50)
= \(\frac { 1 }{ 2 }\) x 22 x 25 = 275 मीटर2
∆EQF का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x ऊँचाई
= \(\frac { 1 }{ 2 }\) x 12 x 50
= 300 मीटर2
आकृति का कुल क्षेत्रफल = (100 + 360 + 60 + 275 + 300) मीटर
= 1095 वर्ग मीटर।
![]()
We hope the RBSE Solutions for Class 8 Maths Chapter 14 क्षेत्रफल Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 14 क्षेत्रफल Additional Questions, drop a comment below and we will get back to you at the earliest.