RBSE Solutions for Class 8 Maths Chapter 14 Area Ex 14.1 is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 14 Area Exercise 14.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | Area |
| Exercise | Exercise 14.1 |
| Number of Questions | 8 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 14 Area Ex 14.1
Question 1.
The length of two perpendicular sides of a trapezium are 10 cm and 16 cm perpendicular distance between them is 8 cm. find the area of the trapezium.
Solution
Area of trapezium
= \(\frac { 1 }{ 2 }\) x (Sum of parallel sides) x height
= \(\frac { 1 }{ 2 }\) x (10 + 16) x 8
= 104 square cm.
Question 2.
The roof of the building is in particular shap(RBSESolutions.com)as shown in the below figure if all the dimension is of equal length then find the area of the whole design.
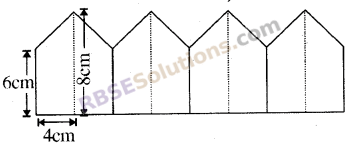
Solution
Every design is a trapezium.
No. of designs = 4
Area of one design
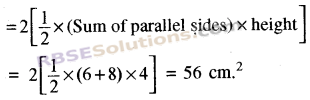
∴ Area of whole design
= 4 x Area of one design
= 4 x 56
= 224 cm²
![]()
Question 3.
The area and height of the trapezium are 34 cm² and 4 cm. One of its parallel side is 10 cm. Find the length of other parallel side.
Solution
Let b cm. be the required length of(RBSESolutions.com)parallel side.
Area of trapezium
= \(\frac { 1 }{ 2 }\) x (Sum of parallel sides) x height
⇒ 34 = \(\frac { 1 }{ 2 }\) x (10 + b) x 4
⇒ 34 x 2 = (10 + b) x 4
⇒ 68 = (10 + b) x 4
⇒ 10 + b = \(\frac { 68 }{ 4 }\)
⇒ 10 + b = 17
⇒ b = 17 – 10
⇒ b = 7
Hence, the length of another parallel side is 7 cm.
![]()
Question 4.
Top surface of a platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
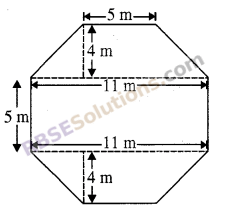
Solution
Required Area
= Area of above trapezium + Area of rectangle + Area of lower trapezium
= \(\frac { 1 }{ 2 }\) x (5 + 11) x 4 + 11 x 5 + \(\frac { 1 }{ 2 }\) x (11 + 5) x 4
Area of trapezium
= \(\frac { 1 }{ 2 }\) x (Sum of parallel sides) x height
Area of rectangle = Length x breadth
= 32 + 55 + 32
= 119 m²
![]()
Question 5.
Length between the opposite vertex of the rhombus shaped plot are 12.5 m and 10.4 m. Find the total cost of making this plot as a flat surface if the cost of(RBSESolutions.com)making a flat surface per square meter is Rs. 180.
Solution
Area of rhombus shaped plot
= \(\frac { 1 }{ 2 }\) x Product of diagonals
= \(\frac { 1 }{ 2 }\) x 12.5 x 10.4
= 65 meter²
Cost of making plane this plot
= 65 x 180
= Rs 11,700
Question 6.
Find the area of the combined rhombus shaped tiles as given in the figure.
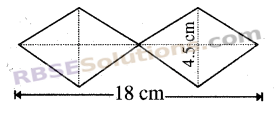
Solution
Area of rhombus shaped tiles
= 2[\(\frac { 1 }{ 2 }\)x(4.5×9)]
Area of rhombus = \(\frac { 1 }{ 2 }\) x Product of diagonals
= 40.5 cm²
![]()
Question 7.
The field of the kalyan is in the form of quadrilateral. The diagonal of this field is 220 m and the perpendiculars dropped on it from the remaining opposite(RBSESolutions.com)vertices are 80 m and 130 m respectively. Find the area of the field.
Solution
Area of quadrilateral shaped farm
= \(\frac { 1 }{ 2 }\) x diagonal x (Sum of perpendiculars drawn from opposite vertices)
= \(\frac { 1 }{ 2 }\) x 220 x (80 + 130)
= \(\frac { 1 }{ 2 }\) x 220 x 210
= 23100 m²
Question 8.
Fill in the blanks
(i) Area of the rhombus is___product of the diagonals.
(ii) Both the diagonals of the scalene quadrilateral is always ___
(iii) Area of the__quadrilateral can be found through the formula height x (sum of parallel sides)/2.
(iv) The quadrilateral(RBSESolutions.com)whose unequal diagonal bisect each other is called___
Solution
(i) half
(ii) unequal
(iii) trapezium
(iv) rhombus.
![]()
We hope the given RBSE Solutions for Class 8 Maths Chapter 14 Area Ex 14.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 14 Area Exercise 14.1, drop a comment below and we will get back to you at the earliest.