RBSE Solutions for Class 8 Maths Chapter 15 Surface Area and Volume Ex 15.1 is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 15 Surface Area and Volume Exercise 15.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 15 |
| Chapter Name | Surface Area and Volume |
| Exercise | Exercise 15.1 |
| Number of Questions | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 15 Surface Area and Volume Ex 15.1
Question 1.
On the basis of given measure determine surface area of cuboidal wooden log, cuboidal brick and box.
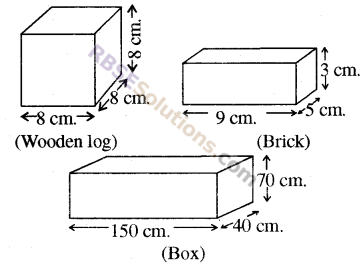
Solution:
(i) Surface area of(RBSESolutions.com)cubical wooden log
= 6 a²
= 6 x (8)²
= 6 x 64
= 384 cm.²
(ii) Surface area of brick
= 2 (lb + bh + hl)
= 2(9 x 5 + 5 x 3 + 3 x 9)
= 2 (45 + 15 + 27)
= 2 (87)
= 174 cm.²
(iii) Surface area of box
= 2 (lb + bh + hl)
= 2 (150 x 40 + 40 x 70 + 70 x 150)
= 2 (6000 + 2800 + 10500)
= 2 (19300)
= 38600 cm.²
![]()
Question 2.
Determine side of a cube whose total surface area is 600 square cm.
Solution:
Let a be the length of side of cube.
Then, total surface area of cube = 6a² cm.²
According to question,
6 a² = 600
a² = \(\frac { 600 }{ 6 }\) = 100
a = √100 = 10 cm
Hence, required(RBSESolutions.com)length of side of cube is 10 cm.
Question 3.
In the given figure whose surface area is more ?
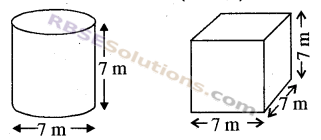
Solution:
For first figure (cylinder)
r = \(\frac { 7 }{ 2 }\) meter
h = 7 meter
∴ Surface Area = 2πr (h + r)
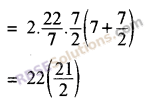
= 231 m²
For second figure (cube) –
a = 7 meter
∴Surface Area = 6 a²
= 6 (7)²
= 6 x 49
= 294 m²
Hence, Surface area of cube is greater than surface area of cylinder..
![]()
Question 4.
Find the area of curved surface if area of base of cylindrical tank is 176 cm.² and height is 30 cm.
Solution
Let r cm be the radius of base.
Then, circumference(RBSESolutions.com)of base = 2πr cm.
According to question,
2πr = 176
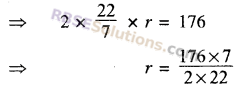
r = 28 cm
h = 30 cm.
Area of curved surface = 2πrh ,
= 2. \(\frac { 22 }{ 7 }\). 28.30
= 5280 cm.²
![]()
Question 5.
Form a sheet of 8 square meter, a closed cylindrical tank is formed which has one meter height and 140 cm diameter.How much sheet will be left after making tank?
Solution
For cylindrical tank diameter = 140 cm.
∴Radius (R) = \(\frac { 140 }{ 2 }\) cm. = 70 cm.
Height (H) = 1 meter = 100 cm.
∴ Surface area of cylindrical tank = 2 πR (H + R)
= 2 . \(\frac { 22 }{ 7 }\) . 70 (100 + 70)
= 74800 cm.²
= \(\frac { 74800 }{ 1000 }\) m²
= 7.48 m²
Surface area(RBSESolutions.com)of metal sheet = 8 m²
∴ Surface area of remaining sheet = 8 – 7.48
= 0.52 m²
![]()
Question 6.
How many paint tins having spread capacity of 100 cm.² will be required to paint external surface of box having dimensions 80 cm x 50 cm x 25 cm.
Solution
Area of outer surface of box
= 2 (lb + bh + hl)
= 2 (80 x 50 + 50 x 25 + 25 x 80)
= 2 (4000 + 1250 + 2000)
= 2 (7250)
= 14500 cm.²
Expansion capacity of 1 paint box = 100 cm.²
∴Required number of boxes
![]()
= \(\frac { 14500 }{ 100 }\)
= 145
![]()
Question 7.
There are 25 cylindrical pillars in a building. Each pillar has radius of 28 cm and height of 4 m. find expenditure of painting curved surface area of all(RBSESolutions.com)pillars at the rate of Rs. 8 per meter square.
Solution
For one cylindrical pillar,
Radius (r) = 28 cm.
Height (h) = 4 m = 4 x 100 cm.
= 400 cm.
∴ Curved surface area of 1 pillar = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 28 x 400
= 70,400 cm.²
∴ Curves surface area of 25 cylindrical pillars = 70400 x 25
= 1760000 cm.²
= \(\frac { 1760000 }{ 1000 }\) m²
= 176 m²
∴ Cost of 25 cylindrical pillars painting = 176 x 8
= Rs 1408
![]()
Question 8.
Curved surface area of a hollow cylinder is 4224 cm². A rectangular sheet having width 33 cm is formed cutting it along its height Find perimeter of sheet
Solution
Let r meter be the radius of base of cylinder and height be the h m. Then,
Surface Area = 2πrh cm²
According(RBSESolutions.com)to question,
⇒ 2πrh = 4224
⇒ 2πr (33) = 4224 | ∵ h = 33cm
⇒ 2πr = \(\frac { 4224 }{ 33 }\)
⇒ 2πr = 128
Perimeter of base = 128cm
Length of sheet (l) = 128 cm
Breadth of sheet (b) = 33 cm
Perimeter of rectangular sheet = 2 (l + b)
= 2 (128 + 33)
= 2 (161)
= 322 cm
![]()
Question 9.
To make a road plain a roller has to complete 750 rounds. If the diameter of roller is 84 cm and length 1 meter then find the area of road.
Solution
For Rollar
Diameter = 84 cm.
Radius (r) = \(\frac { 84 }{ 2 }\) cm. = 42 cm.
Length (h) = 1 meter = 100 cm.
∴ Curved(RBSESolutions.com)surface area = 2πrh
= 2 . \(\frac { 22 }{ 7 }\) . 42 . 100
= 26400 cm.²
∴ Area of road made plane in one round = 26400 cm.²
∴ Area of road = 26400 x 750
= 19800000 cm.²
= \(\frac { 19800000 }{ 10000 }\) m²
= 1980 m²
![]()
Question 10.
A cube is made by arranging 64 cubes having side of 1 cm, find total surface area of cube so formed.
Solution
Side of one cube = 1 cm.
∴Volume of one cube = a³ = (1)³
= 1 cm³
∴ Volume of 64 cubes = 64 x 1 = 64 cm.³
Let the side of new cube = x cm.
∴ Volume(RBSESolutions.com)of new cube = Volume of 64 cubes
∴ x³ = 64
=> x = (64)1/3 = 4 cm.
On comparing
x = 4
∴ Total surface area of new cube
= 6a2 = 6 x (4)2
= 6 x 16 = 96 cm.2
![]()
We hope the given RBSE Solutions for Class 8 Maths Chapter 15 Surface Area and Volume Ex 15.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 15 Surface Area and Volume Exercise 15.1, drop a comment below and we will get back to you at the earliest.