RBSE Solutions for Class 8 Maths Chapter 16 Data Handling Ex 16.2 is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 16 Data Handling Exercise 16.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 16 |
| Chapter Name | Data Handling |
| Exercise | Exercise 16.2 |
| Number of Questions | 6 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 16 Data Handling Ex 16.2
Question 1.
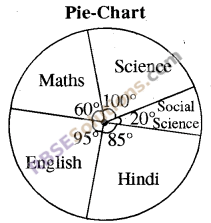
Number of text books of any school is given below. Represent this data through pie chart
| Subject | Science | Maths | English | Hindi | Social Science | Total |
| No of Books | 200 | 120 | 190 | 170 | 40 | 720 |
Solution:
| Subject | Number of Books | Part of Total | Part of 360° |
| Science | 200 | \(\frac { 200 }{ 720 } =\frac { 5 }{ 18 } \) | \({ 360 }^{ o }\times \frac { 5 }{ 18 } ={ 100 }^{ o }\) |
| Maths | 120 | \(\frac { 120 }{ 720 } =\frac { 1 }{ 6 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 6 } ={ 60 }^{ o }\) |
| English | 190 | \(\frac { 190 }{ 720 } =\frac { 19 }{ 72 } \) | \({ 360 }^{ o }\times \frac { 19 }{ 72 } ={ 95 }^{ o }\) |
| Hindi | 170 | \(\frac { 170 }{ 720 } =\frac { 17 }{ 72 } \) | \({ 360 }^{ o }\times \frac { 17 }{ 72 } ={ 85 }^{ o }\) |
| Social Science | 40 | \(\frac { 40 }{ 720 } =\frac { 1 }{ 18 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 18 } ={ 20 }^{ o }\) |
| Total | 720 | 1 | 360° |
![]()
Question 2.
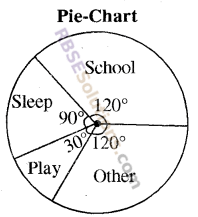
Description of daily activities of a child is as follows. Represent this data in the form of pie chart
| Time spent | School | Sleep | Play | Other |
| Hours | 8 Hours | 6 Hours | 2 Hours | 8 Hours |
Solution:
| Time Spent | Hours | Part of Whole | Part of 360° |
| School | 8 | \(\frac { 8 }{ 24 } =\frac { 1 }{ 3 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 3 } ={ 120 }^{ o }\) |
| Sleep | 6 | \(\frac { 6 }{ 24 } =\frac { 1 }{ 4 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 4 } ={ 90 }^{ o }\) |
| Play | 2 | \(\frac { 2 }{ 24 } =\frac { 1 }{ 12 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 12 } ={ 30 }^{ o }\) |
| Other | 8 | \(\frac { 8 }{ 24 } =\frac { 1 }{ 3 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 3 } ={ 120 }^{ o }\) |
| Total | 24 | 1 | 360° |
![]()
Question 3.
Pie chart shows marks obtained by student in various subjects Hindi, English,Mathematics, Social Science and Science.
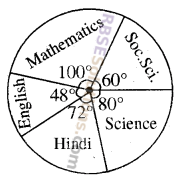
If total marks obtained by these students are 900 then answer the following questions
(i) In which subject did student have 250 marks?
(ii) That student(RBSESolutions.com)obtained how many marks more in mathematics as compared to Hindi?
(iii) Check whether total marks obtained in Social Science and Mathematics is more than total of marks obtained in English and Hindi?
Solution:
(i) Part of whole = \(\frac { 250 }{ 900 }\)
∴Part of 360° = \(\frac { 250 }{ 900 }\) x 360°
= 100°
Hence, student has obtained 250 marks in Maths.
(ii) Marks obtained in Maths = 250
Marks obtained in Hindi
= \(\frac { 72 }{ 360 }\) x 900
= 180
∴Difference of marks between Maths and Hindi = 250 – 180 = 70
(iii) Marks obtained in Social Science
= \(\frac { 60 }{ 360 }\) x 900
= 150
Marks obtained in Maths = 250
∴The sum of marks obtained in Social Science and Maths : 150 + 250 = 400
Marks obtained in English
= \(\frac { 48 }{ 360 }\) x 900 = 120
Marks obtained in Hindi = 180
∴Sum of(RBSESolutions.com)marks obtained in English and Hindi = 120 + 180 = 300
Hence, the sum of marks obtained in Social Science and Maths is more than the sum of marks obtained in English and Hindi.
![]()
Question 4.
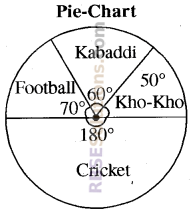
Draw a pie chart showing following information. This table shows games liked by student of a class.
| Game | Kho-Kho | Kabaddi | Football | Cricket |
| No of Students | 5 | 6 | 7 | 18 |
Solution:
| Sport | No of Students | Part of Whole | Part of 360° |
| Kho-Kho | 5 | \(\frac { 5 }{ 36 }\) | \({ 360 }^{ o }\times \frac { 5 }{ 36 } ={ 50 }^{ o }\) |
| Kabaddi | 6 | \(\frac { 6 }{ 36 } =\frac { 1 }{ 6 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 6 } ={ 60 }^{ o }\) |
| Football | 7 | \(\frac { 7 }{ 36 }\) | \({ 360 }^{ o }\times \frac { 7 }{ 36 } ={ 70 }^{ o }\) |
| Cricket | 18 | \(\frac { 18 }{ 36 } =\frac { 1 }{ 2 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 2 } ={ 180 }^{ o }\) |
| Total | 36 | 1 | 360° |
![]()
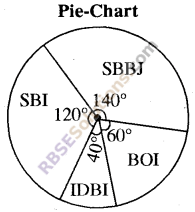
Question 5.
In accordance to ‘Jan Dhan Yojna of Indian government number of accounts opened(RBSESolutions.com)by following banks in one month in Kota city is as follows. Draw a pie-chart
| Name of Bank | SBBJ | SBI | IDBI | BOI |
| Number of Accounts opened | 21000 | 18000 | 6000 | 9000 |
Solution:
| Name of Bank | Number of Accounts opened | Part of Whole | Part of 360° |
| SBBJ | 21000 | \(\frac { 21000 }{ 54000 } =\frac { 7 }{ 18 } \) | \({ 360 }^{ o }\times \frac { 7 }{ 18 } ={ 140 }^{ o }\) |
| SBI | 18000 | \(\frac { 18000 }{ 54000 } =\frac { 1 }{ 3 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 3 } ={ 120 }^{ o }\) |
| IDBI | 6000 | \(\frac { 6000 }{ 54000 } =\frac { 1 }{ 9 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 9 } ={ 40 }^{ o }\) |
| BOI | 9000 | \(\frac { 9000 }{ 54000 } =\frac { 1 }{ 6 } \) | \({ 360 }^{ o }\times \frac { 1 }{ 6 } ={ 60 }^{ o }\) |
| Total | 54000 | 1 | 360° |
![]()
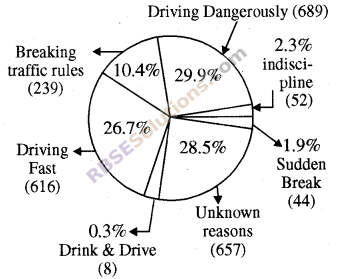
Question 6
Various mistakes of automobile drivers are shown in pie chart With the help of pie chart answer the following questions
(i) Percentage of accidents by driving vehicle with fast speed?
(ii) Due to which mistake of(RBSESolutions.com)automobile driver maximum accidents take place?
(iii) How many accidents occur due to driving of automobile in drunken state?
(iv) How many people underwent accident due to disobedience of traffic rules?
Solution:
(i) 26.7%
(ii) Driving dangerously (29.9%)
(iii) 0.3%
(iv) 10.4%
![]()
We hope the given RBSE Solutions for Class 8 Maths Chapter 16 Data Handling Ex 16.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 16 Data Handling Exercise 16.2, drop a comment below and we will get back to you at the earliest.