RBSE Solutions for Class 8 Maths Chapter 2 घन एवं घनमूल Ex 2.1

RBSE Solutions for Class 8 Maths Chapter 2 घन एवं घनमूल Ex 2.1 is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 2 घन एवं घनमूल Exercise 2.1.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 8
Subject	Maths
Chapter	Chapter 2
Chapter Name	घन एवं घनमूल
Exercise	Exercise 2.1
Number of Questions	4
Category	RBSE Solutions

Rajasthan Board RBSE Class 8 Maths Chapter 2 घन एवं घनमूल Ex 2.1

प्रश्न 1
निम्नलिखित में से कौनसी संख्याएँ पूर्ण घन नहीं हैं
(i) 512
(ii) 243
(iii) 1000
(iv) 100
(v) 2700
हल:
(i) 512
अभाज्य गुणनखण्ड करने पर

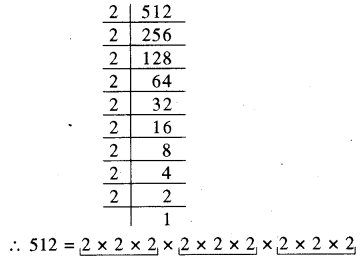
अभाज्य गुणनखण्ड में तीन-तीन संख्याओं का समूह बनाया जा सकता है। (RBSESolutions.com)अतः 512 एक पूर्ण घन संख्या है।

(ii) 243 अभाज्य गुणनखण्डे करने पर

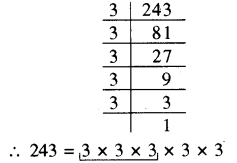
अभाज्य गुणनखण्ड में तीन-तीन संख्याओं का(RBSESolutions.com) समूह नहीं बनाया जा सकता है। अत: 243 एक पूर्ण घन संख्या नहीं।

(iii) 1000
अभाज्य गुणनखण्ड करने पर

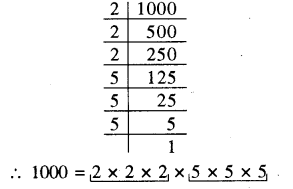
अभाज्य गुणनखण्ड में तीन-तीन संख्याओं का(RBSESolutions.com) समूह बनाया जा सकता है। अतः 1000 एक पूर्ण घन संख्या है।

(iv) 100
अभाज्य गुणनखण्ड करने पर

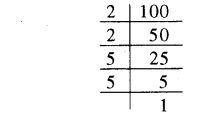
∴100 = 2 x 2 x 5 x 5
अभाज्य गुणनखण्ड में 2 और 5 के तीन-तीन के समूह पूरे नहीं हो पा रहे हैं। अतः 100 एक पूर्ण घन संख्या नहीं है।

(v) 2700
अभाज्य गुणनखण्ड करने पर

अभाज्य गुणनखण्ड में 3 का तो तीन-तीन का समूह है।
परन्तु 2 और 5 के तीन-तीन के समूह पूरे नहीं हो पा रहे हैं।(RBSESolutions.com) अतः 2700 एक पूर्ण घन संख्या नहीं है।

प्रश्न 2
वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्याओं को गुणा करने पर पूर्ण घन प्राप्त हो जाए
(i) 108
(ii) 500
(iii) 5400
(iv) 10584
हल:
(i) 108 अभाज्य गुणनखण्ड करने पर

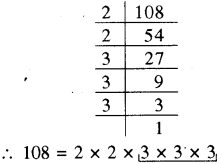
अभाज्य गुणनखण्ड में 3 का तो तीन-तीन का समूह है। परन्तु 2 का तीन-तीन का समूह पूरा नहीं हो पा रहा है। अतः 108 एक पूर्ण घन संख्या नहीं है। इसे पूर्ण घन संख्या बनाने के लिए 2 से गुणा(RBSESolutions.com) करना होगा, जिससे 2 का तीन-तीन का समूह पूरा हो जाएगा। अतः अभीष्ट सबसे छोटी संख्या 2 है।

(ii) 500
अभाज्य गुणनखण्ड करने पर

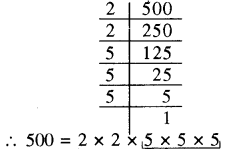
अभाज्य गुणनखण्ड में 5 का तो तीन-तीन का समूह है। परन्तु 2 का तीन-तीन का समूह पूरा नहीं हो पा रहा है। अतः 500 एक पूर्ण घन संख्या नहीं है। इसे पूर्ण घन संख्या बनाने के लिए 2 से गुणा करना होगा(RBSESolutions.com) जिससे 2 का तीन-तीन का समूह पूरा हो जाएगा। अतः अभीष्ट सबसे छोटी संख्या 2 है।

(iii) 5400
अभाज्य गुणनखण्ड करने पर

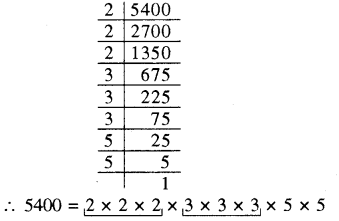
अभाज्य गुणनखण्ड में 2 और 3 के तो तीन-तीन के समूह हैं परन्तु 5 का तीन-तीन का समूह पूरा नहीं हो पा रहा है। अतः 5400 एक पूर्ण घन संख्या नहीं है। इसे पूर्ण घन संख्या बनाने के लिए 5 (RBSESolutions.com)से गुणा करना होगा जिससे 5 का तीन-तीन का समूह पूरा हो जाये। अतः अभीष्ट सबसे छोटी संख्या 5 है।

(iv) 10584
अभाज्य गुणनखण्ड करने पर


अभाज्य गुणनखण्ड में 2 तथा 3 के तीन-तीन के समूह हैं। परन्तु 7 का तीन-तीन का समूह पूरा नहीं हो पा रहा है।
अतः 10584 एक पूर्ण घन संख्या नहीं है। इसे पूर्ण घन(RBSESolutions.com) संख्या बनाने के लिए 7 से गुणा करना होगा जिससे 7 का तीन-तीन का समूह पूरा हो जाए।
अतः अभीष्ट सबसे छोटी संख्या 7 है।

प्रश्न 3
वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्याओं को भाग देने पर एक पूर्ण घन प्राप्त होगा।
(i) 24
(ii) 250
(iii) 192
(iv) 135
हल:
(i) 24
अभाज्य गुणनखण्ड करने पर

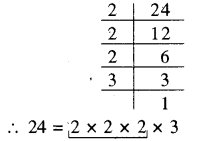
अभाज्य गुणनखण्ड में 2 तीन-तीन के समूह में है परन्तु 3 का तीन-तीन का समूह पूरा नहीं हो पा रहा है। अतः 24 एक पूर्ण घन संख्या नहीं है।

24 के अभाज्य गुणनखण्ड में अभाज्य गुणनखण्ड 3 केवल एक बार आ रहा है। अतः यदि हम 24 को 3 से भाग दें तो भागफल के अभाज्य गुणनखण्ड में 3 नहीं आयेगा। अतः वह सबसे छोटी संख्या 3 होगी जिससे 24 का भाग(RBSESolutions.com) देने पर भागफल एक पूर्ण घन संख्या प्राप्त होगी।
साथ ही परिणामी पूर्ण घन संख्या = 243 = 8 = 23

(ii) 250
अभाज्य गुणनखण्ड करने पर

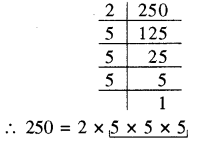
अभाज्य गुणनखण्ड 5 तीन-तीन के समूह में है परन्तु 2 का तीन-तीन का समूह पूरा नहीं हो पा रहा है। अतः 250 एक पूर्ण घन संख्या नहीं है।
250 के अभाज्य गुणनखण्ड में अभाज्य गुणनखण्ड 2 केवल एक बार आ रहा है। अतः यदि हम 250 को 2 से भाग दें तो भागफल के अभाज्य गुणनखण्ड में 2 नहीं आयेगा। अतः वह सबसे छोटी संख्या 2 होगी जिससे 250 को भाग देने पर भागफल एक पूर्ण घन संख्या प्राप्त होगा।
साथ ही परिणामी पूर्ण घन संख्या = 250 + 2 = 125 = 5³

(iii) 192
अभाज्य गुणनखण्ड करने पर

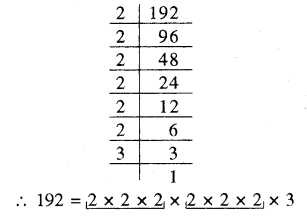
अभाज्य गुणनखण्ड में 2 और 2 तीन-तीन के समूह में हैं। परन्तु 3 का तीन-तीन का समूह पूरा नहीं हो पा रहा है।
अतः 192 एक पूर्ण घन संख्या नहीं है।
192 के अभाज्य गुणनखण्ड में 3 केवल एक बार आ रहा है। (RBSESolutions.com) अतः यदि हम 192 को 3 से भाग दें तो भागफल के अभाज्य गुणनखण्ड में 3 नहीं आयेगा। अतः वह सबसे छोटी संख्या 3 होगी जिससे 192 को भाग देने पर भागफल एक पूर्ण घन संख्या प्राप्त होगा।
साथ ही परिणामी पूर्ण घन संख्या = 192 ÷ 3 = 64 = (2 x 2)³ = 4³

(iv) 135
अभाज्य गुणनखण्ड करने पर

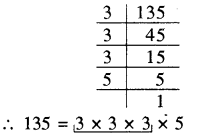
अभाज्य गुणनखण्ड में 3 तीन-तीन के समूह में है परन्तु 5 का तीन-तीन का समूह पूरा नहीं हो पा रहा है। अतः 135 एक पूर्ण घन संख्या नहीं है।
135 के अभाज्य गुणनखण्ड में अभाज्य गुणनखण्ड 5 केवल एक बार आ रहा है। अतः यदि हम 135 को 5 से भाग दें तो भागफल के अभाज्य गुणनखण्ड में 5 नहीं आयेगा। अतः वह सबसे छोटी संख्या 5 होगी जिससे 135 को भाग देने पर भागफल एक पूर्ण घन संख्या प्राप्त होगा।
साथ ही परिणामी पूर्ण घन संख्या = 135 ÷ 5 = 27 = 3³

प्रश्न 4
रेहान एक साबुन फैक्ट्री में काम करता है, वह घनाकार साबुन को जमाकर घन बनाकर खेल रहा है। बताइए यदि 216 साबुन जमाने हों तो बनने वाले घन की पहली पंक्ति में कितने साबुन होंगे?
हल:
कुल साबुन = 216
अभाज्य गुणनखण्ड करने पर

अतः घन की पहली पंक्ति में 6 साबुन होंगे।

We hope the RBSE Solutions for Class 8 Maths Chapter 2 घन एवं घनमूल Ex 2.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 2 घन एवं घनमूल Exercise 2.1 , drop a comment below and we will get back to you at the earliest.