RBSE Solutions for Class 8 Maths Chapter 8 ठोस आकारों का चित्रण Additional Questions is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 8 ठोस आकारों का चित्रण Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 8 |
| Chapter Name | ठोस आकारों का चित्रण |
| Exercise | Additional Questions |
| Number of Questions | 37 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 8 ठोस आकारों का चित्रण Additional Questions
I. बहुविकल्पात्मक प्रश्न
प्रश्न 1
समतल आकृतियाँ कहलाती हैं –
(a) बहुआयामी
(b) त्रि-विमीय
(c) द्वि-विमीय
(d) उपर्युक्त में से कोई नहीं
प्रश्न 2
घनाभ में शीर्षों(RBSESolutions.com)की संख्या होती है –
(a) 12
(b) 8
(c) 6
(d) 4
प्रश्न 3
प्रत्येक ठोस बहुभुजीय(RBSESolutions.com)क्षेत्रों से मिलकर बनता है। ये क्षेत्र कहलाते हैं –
(a) किनारे
(b) शीर्ष
(c) फलक
(d) घनाभ
प्रश्न 4
ऑयलर सूत्र होता है –
(a) F + V = E + 2
(b) F – V = E – 2
(c) V + E = F + 2
(d) V – E = F – 2
![]()
प्रश्न 5
किसी आकृति के किनारे या कोर जिन बिन्दुओं पर मिलते हैं, वे कहलाते हैं –
(a) फलक
(b) सतहे
(c) शीर्ष
(d) पिरामिड
प्रश्न 6
त्रि-विमीय(RBSESolutions.com)आकृति का उदाहरण है –
(a) त्रिभुज
(b) समचतुर्भुज
(c) आयत
(d) गोला
प्रश्न 7
एक पासे में फलकों की संख्या है –
(a) 2
(b) 4
(c) 6
(d) 3
प्रश्न 8
एक शंकु में शीर्षों की संख्या है –
(a) 1
(b) 2
(c) 3
(d) इनमें से कोई नहीं
![]()
प्रश्न 9
घन के किनारों की संख्या होती है –
(a) 8
(b) 12
(c) 6
(d) 14
प्रश्न 10
घन में फलकों की संख्या होती है –
(a) 12
(b) 8
(c) 6
(d) 10
उत्तरमाला:
1. (c) 2. (b) 3. (c) 4. (a) 5. (c) 6. (d) 7. (c) 8. (a) 9. (b) 10. (c)
II. रिक्त स्थानों की पूर्ति कीजिए
1. घनाभ एक ………. आकृति होती है।
2. भिन्न-भिन्न स्थानों से त्रिविमीय वस्तुओं के ……………….. दृश्य मिलते हैं।
3. किसी भी बहुफलक(RBSESolutions.com)के लिए F + V =…….. सत्य होता है।
4. ………… पिरामिड चतुष्फलक कहलाता है।
5. ……………….. प्रिज्म घन कहलाता है।
उत्तरमाला:
1. त्रि-विमीय 2. भिन्न-भिन्न 3. E + 2 4. त्रिभुजाकार 5. वर्गाकार।
![]()
III. सत्य/असत्य
1. पंचभुजाकार पिरामिड में 6 शीर्ष होते हैं।
2. आयताकार पिरामिड में 5 शीर्ष होते हैं।
3. एक शंकु में दो(RBSESolutions.com)फलक होते हैं।
4. वह ठोस जिसमें कोई शीर्ष और कोई किनारा नहीं होता है, गोला कहलाता है।
5. बिना शीर्ष और आधार के एक बेलन का जाल वृत्त होता है।
उत्तरमाला:
1, सत्य 2. सत्य 3. सत्य 4. सत्य 5. असत्य।
IV. अतिलघूत्तरात्मक प्रश्न
प्रश्न 1
एक त्रिभुजाकार प्रिज्म में किनारों तथा फलकों की संख्या लिखिए।
उत्तर:
एक त्रिभुजाकार प्रिज्म में किनारों की संख्या = 9
एवं फलकों की संख्या = 5
प्रश्न 2
क्या एक वर्ग प्रिज्म और एक घन एक ही होते हैं? स्पष्ट कीजिए।
हल:
नहीं। एक वर्ग प्रिज्म और एक घन एक नहीं होते। हैं। एक वर्ग प्रिज्म एक घनाभ भी हो सकता है।
![]()
प्रश्न 3
त्रि-विमीय आकार किसे कहते हैं ?
हल:
ठोसों के ऐसे आकार जिनमें(RBSESolutions.com)लम्बाई, चौड़ाई व ऊँचाई (या गहराई) तीनों माप पाए जाते हैं, त्रि-विमीय आकार कहलाते हैं।
प्रश्न 4
द्वि-विमीय आकार को परिभाषित कीजिए।
हल:
वह समतलीय आकार जिसमें लम्बाई और चौड़ाई जैसे दो माप(RBSESolutions.com)होते हैं, द्वि-विमीय आकार कहलाता है।
प्रश्न 5
द्वि-विमीय आकारों के तीन उदाहरण लिखिए।
हल:
त्रिभुज, आयत, वृत्त।
![]()
प्रश्न 6
त्रि-विमीय आकारों के तीन उदाहरण लिखिए।
हल:
घन, गोला, बेलनं।
प्रश्न 7
समबहुफलक को परिभाषित कीजिए।
हल:
वह बहुफलक जिसके सभी सर्वांगसम बहुभुजों से बने हों(RBSESolutions.com)तथा प्रत्येक शीर्ष पर मिलने वाले फलकों की संख्या समान हो, समबहुफलक कहलाता है।
![]()
V. लघूत्तरात्मक प्रश्न
प्रश्न 1
प्रिज्म और बेलन किस प्रकार एक जैसे हैं?
हल:
एक प्रिज्म एक बेलन तब हो जाता है जब उसके आधार की भुजाओं की संख्या अपरिमित रूप से अधिक हो जाती है।
प्रश्न 2
पिरामिड और शंकु किस प्रकार एक जैसे हैं?
हल:
एक पिरामिड एक शंकु तब हो जाता है जब(RBSESolutions.com)उसके आधार की भुजाओं की संख्या अपरिमित रूप से अधिक हो जाती है।
प्रश्न 3
निम्न ठोसों के लिए ऑयलर सूत्र का सत्यापन कीजिए
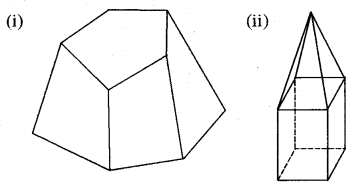
हल:
(i) इस आकृति में
F = 7
V = 10
E = 15
∴ F+ V = 7 + 10 = 17
और E + 2 = 15 + 2 = 17
अतः, F+ V = E + 2
अतः ऑयलर का सूत्र(RBSESolutions.com)सत्यापित होता है।
![]()
(ii) इस आकृति में।
F = 9
V = 9
E = 16
∴ F + V = 9+ 9 = 18
और E + 2 = 16 + 2 = 18
अतः, F + V = E + 2
अतः ऑयलर का सूत्र सत्यापित होता है।
प्रश्न 4
क्या किसी बहुफलक(RBSESolutions.com)के 10 फलकें, 20 किनारे तथा 15 शीर्ष हो सकते हैं?
हल:
F = 10
E = 20
V = 15
∴ F + V = 10 + 15 = 25
E + 2 = 20 + 2 = 22
∴ F+ V ≠ E + 2
∴ ऐसा बहुफलक नहीं हो सकता है।
प्रश्न 5
ऑयलर सूत्र का प्रयोग करते हुए, अज्ञात संख्या को ज्ञात कीजिए
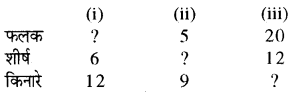
हल:
(i) F + V = E + 2
⇒ F + 6 = 12 + 2
⇒ F + 6 = 14
⇒ F = 14 – 6 = 8
(ii) F+ V = E + 2
⇒ 5 + V = 9+ 2
⇒ 5 + V= 11
⇒ V = 11 – 5 = 6
(iii) F + V = E + 2
⇒ 20 + 12 = E + 2
⇒ 32 = E + 2
⇒ E = 32 – 2 = 30
![]()
प्रश्न 6
एक घन के एक शीर्ष को उसकी तीनों भुजाओं से बराबर दूरी से चित्र में दिखाए अनुसार काटा जाता है। नई बनने वाली आकृति में कितने शीर्ष, कितने फलक व(RBSESolutions.com)कितने कोरें होंगी?
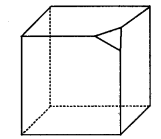
हल:
शीर्षों की संख्या = 10
फलकों की संख्या = 7
किनारों की संख्या = 15
![]()
प्रश्न 7
आप कैसा प्रतिच्छेद प्राप्त करते हैं यदि निम्न ठोसों को (i) ऊर्ध्वाधरतः (ii) क्षैतिजतः काटा जाता है ?
(1) एक पासा
(2) एक वृत्ताकार पाइप
(3) एक गोल सेबे
(4) एक(RBSESolutions.com)आइसक्रीम शंकु।
हल:

प्रश्न 8
किसी बहुफलक में शीर्षों की संख्या 10 एवं किनारों की संख्या 16 है तो उसके फलकों की संख्या ज्ञात कीजिए।
हल:
शीर्षों की संख्या (V) = 10
किनारों की(RBSESolutions.com)संख्या (E) = 16
फलकों की संख्या (F) ज्ञात करनी है।
आयलर सूत्र : V+ F = E + 2
तब, 10 + F = 16 + 2
या, F = 16 + 2 – 10
या, F = 8
![]()
प्रश्न 9
किसी बहुफलक में शीर्षों की संख्या 9 तथा फलकों की संख्या 9 है तो उसके किनारों की संख्या ज्ञात कीजिए।
हल:
शीर्षों की संख्या (V) = 9
फलकों की संख्या (F) = 9
किनारों (E) की संख्या ज्ञात करनी है।
आयलर सूत्र : V + F = E + 2
तब 9 + 9 = E + 2
या 9 +9 – 2 = E
अतः E = 16
प्रश्न 10
किसी बहुफलक में फलकों (Faces) की संख्या(RBSESolutions.com)5 एवं किनारों (Edges) की संख्या 9 है, तो शीर्षों (Vertices) की संख्या ज्ञात कीजिए।
हल:
फलकों की संख्या (F) = 5
किनारों की संख्या (E) = 9
शीर्षों की संख्या (V) = ?
हम जानते हैं
ऑयलर सूत्र से, F + V = E + 2
5 + V = 9 + 2
5 + y = 11
V = 11 – 5
V = 6
अतः शीर्षों (V) की संख्या = 6
![]()
We hope the RBSE Solutions for Class 8 Maths Chapter 8 ठोस आकारों का चित्रण Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 8 ठोस आकारों का चित्रण Additional Questions, drop a comment below and we will get back to you at the earliest.