RBSE Solutions for Class 9 Maths Chapter 10 Area of Triangles and Quadrilaterals Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 10 Area of Triangles and Quadrilaterals Additional Questions.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 10 |
| Chapter Name | Area of Triangles and Quadrilaterals |
| Exercise | Additional Questions |
| Number of Questions Solved | 28 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 10 Area of Triangles and Quadrilaterals Additional Questions
Multiple Choice Questions
Question 1.
The area of a parallelogram and a triangle are equal. If their base (RBSESolutions.com) is common and altitude of parallelogram is 2 cm, then altitude of the triangle is:
(A) 4 cm
(B) 2 cm
(C) 1 cm
(D) 3 cm
Solution
(A) 4 cm
Question 2.
Let ABCD be a parallelogram and ABEF be a rectangle with EF lying along the line CD. If AB = 7 cm and BE = 6.5 cm, then area of the parallelogram is:
(A) 22.75 cm²
(B) 11.375 cm²
(C) 45.5 cm²
(D) 45 cm²
Solution
(C) 45.5 cm²
![]()
Question 3.
Two parallelograms are on the same (RBSESolutions.com) base and between the same parallels. Then ratio between their areas is:
(A) 2 : 1
(B) 1 : 1
(C) 1 : 2
(D) 3 : 1
Solution
(B) 1 : 1
Question 4.
In the adjoining figure, ABCD is a rectangle with AE = EF = FB then the ratio of the area of the triangle CEF and that of the rectangle ABCD is:
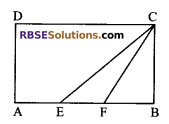
(A) 1 : 4
(B) 1 : 6
(C) 2 : 5
(D) 2 : 3
Solution
(B) 1 : 6
Question 5.
In the given figure, if area (RBSESolutions.com) of the parallelogram ABCD is 30 cm², then ar (∆ADE) + ar (∆BCE) is equal to:
(A) 20 cm²
(B) 30 cm²
(C) 15 cm²
(D) 25 cm²
Solution
(C) 15 cm²
Question 6.
In figure, ABCD is a parallelogram if (RBSESolutions.com) area of ∆AEB is 16 cm², then area of ∆BFC is:
(A) 32 cm²
(B) 24 cm²
(C) 8 cm²
(D) 16 cm²
Solution
(D) 16 cm²
Question 7.
In the figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, then AD is equal to:
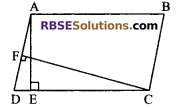
(A) 1.28 cm
(B) 12.8 cm
(C) 6.4 cm
(D) 14.4 cm
Solution
(B) 12.8 cm
![]()
Question 8.
In the given figure, ABCD is a parallelogram (RBSESolutions.com) whose area is 20 cm² then area of ∆AOD is:
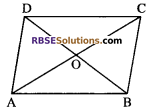
(A) 10 cm²
(B) 15 cm²
(C) 5 cm²
(D) 12 cm²
Solution
(C) 5 cm²
Question 9.
AD is a median of ∆ABC. If area (RBSESolutions.com) of ∆ABD is 25 cm² then area of ∆ABC would be:
(A) 100 cm²
(B) 25 cm²
(C) 75 cm²
(D) 50 cm²
Solution
(D) 50 cm²
Question 10.
In an ∆ABC, E is the mid-point of median AD, then ar (∆BED) is:
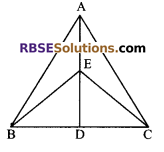
Solution
(C) \(\frac { 1 }{ 4 }\) ar(∆ABC)
Very Short Answer Type Questions
Question 1.
In parallelogram ABCD, AB = 12 cm. The altitudes (RBSESolutions.com) corresponding to the two sides AB and AD are 8 cm and 10 cm respectively. Compute BC.
Solution.
Area of parallelogram ABCD = base x corresponding altitude = AB x CM = 12 cm x 8 cm = 96 cm2
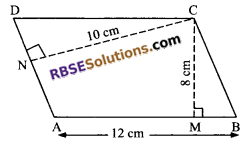
Again area of parallelogram ABCD = BC x CN
⇒ 96 = BC x 10
⇒ BC = 9.6 cm.
Question 2.
If the ratio of the altitude and the area of the (RBSESolutions.com) parallelogram is 2 : 11, then find the length of the base of the parallelogram.
Solution.
Here we are given that
altitude : area = 2 : 11
altitude = 2x and area = 11x (say)
Then, area = base x altitude
11x = base x 2x
⇒ base = \(\frac { 11x }{ 2x }\) = 5.5 units
![]()
Question 3.
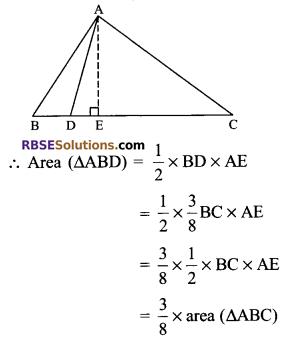
In figure, D divides the side BC of ∆ABC in (RBSESolutions.com) the ratio 3 : 5. Show that ar (∆ABD) = \(\frac { 3 }{ 8 }\) ar (∆ABC)
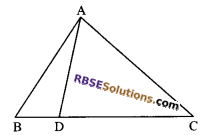
Solution.
We are given that D divides BC in the ratio 3 : 5
i.e. BD : CD = 3 : 5
⇒ BD = \(\frac { 3 }{ 8 }\) DC …(i)
Draw AE ⊥ BC
Question 4.
In ∆ABC (see figure), E is the mid-point of the (RBSESolutions.com) median AD. If area of the triangle ABC is 184 sq. units, find area of ∆DEC.
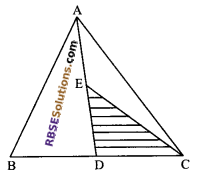
Solution.
Since AD is the median of ∆ABC
ar (∆ADC) = \(\frac { 1 }{ 2 }\) ar (∆ABC) = \(\frac { 1 }{ 2 }\) x 184 = 92 sq. unit.
Again E is the mid-point of side AD.
CE divides AADC into two parts equal in area.
area ∆DEC = \(\frac { 1 }{ 2 }\) (ar ∆ADC) = \(\frac { 1 }{ 2 }\) x 92 = 46 sq. unit.
Question 5.
In figure, area (∆BCE) = 75.2 m2. Find the area (RBSESolutions.com) of parallelogram ABCD.
Solution.
If a triangle and a parallelogram are on the same base and between the same parallels, then the area of triangle is equal to half the area of parallelogram.
i.e Area of ∆BCE = \(\frac { 1 }{ 2 }\) ar (||gm ABCD)
⇒ 75.2 m2 = \(\frac { 1 }{ 2 }\) ar(||gm ABCD)
⇒ ar (||gm ABCD) = 75.2 x 2 m2 = 150.4 m2.
Question 6.
Prove that a median of a triangle divides it (RBSESolutions.com) into two triangles of equal area.
Solution.
Given: A triangle PQR in which RS is a median
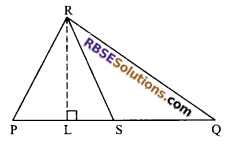
To prove: ar (∆RPS) = ar (∆RSQ)
Construction: Draw RL ⊥ PQ
Proof: RS is median
⇒ PS = SQ
⇒ \(\frac { 1 }{ 2 }\) x PS x RL = \(\frac { 1 }{ 2 }\) x SQ x RL
⇒ ar (∆RPS) = ar (∆RSQ)
Question 7.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect (RBSESolutions.com) each other at O. Prove that ar (∆AOD) = ar (∆BOC).
Solution.
Since ∆ACD and ∆BDC are on the same base CD and between the same parallels AB and CD.

Therefore, ar (∆ACD) = ar (∆BDC)
Subtracting ar (∆ACD) from both side, we get
ar (∆ACD) – ar (∆COD) = ar (∆BDC) – ar (∆COD)
⇒ ar (∆AOD) = ar (∆BOC)
![]()
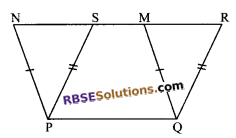
Question 8.
Two parallelograms PQRS and PQMN have (RBSESolutions.com) common base PQ as shown in figure. PQ = 9 cm, SM = 3 cm, and ST = 5 cm. Find the area of PQRN.
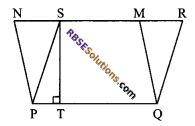
Solution.
Since parallelograms PQRS and PQMN are on the same base PQ and between the same parallels PQ and NR.
ar (PQRS) = ar (PQMN) = 9 x 5 = 45 cm2
Also, area of trapezium PQMS
= \(\frac { 1 }{ 2 }\) x (PQ + MS) x ST
= \(\frac { 1 }{ 2 }\) x (9 + 3) x 5
= \(\frac { 1 }{ 2 }\) x 12 x 5 =30 cm2
ar (PQRN) = ar (PQRS) + ar (PQMN) – ar (PQMS) = (45 + 45 – 30) cm2 = 60 cm2
Question 9.
In figure, ABCD is a quadrilateral in which (RBSESolutions.com) diagonal BD =14 cm. If AL ⊥ BD and CM ⊥ BD such that AL = 8 cm and CM = 6 cm, find the area of quadrilateral ABCD.
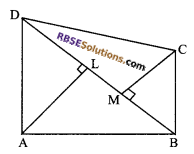
Solution.
Here we are given that BD = 14 cm
AL ⊥ BD and CM ⊥ BD and AL = 8 cm, CM = 6 cm
Area of quadrilateral ABCD = ar (∆ABD) + ar (∆BDC)
= \(\frac { 1 }{ 2 }\) x BD x AL + \(\frac { 1 }{ 2 }\) x BD x CM
= \(\frac { 1 }{ 2 }\) x BD x (AL + CM)
= \(\frac { 1 }{ 2 }\) x 14 x (8 + 6)
= \(\frac { 1 }{ 2 }\) x 14 x 14 = 98 cm2
Question 10.
In figure, ABCD is a quadrilateral. BP is drawn (RBSESolutions.com) parallel to AC and BP meets DC produced at P. Prove that ar (∆ADP) = ar (quad. ABCD).
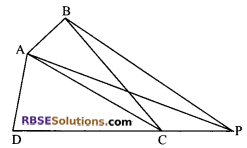
Solution.
Here ∆ABC and ∆ACP are on the same base AC and between the same parallels AC and BP.
Therefore,
ar (∆ABC) = ar (∆ACP)
⇒ ar (∆ADC) + ar (∆ABC) = ar (∆ADC) + ar (∆ACP)
⇒ ar (quad. ABCD) = ar (∆ADP)
Hence, ar (∆ADP) = ar (quad. ABCD)
Short Answer Type Questions
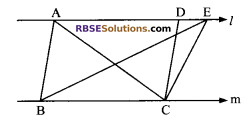
Question 1.
XY is a line parallel to side BC of (RBSESolutions.com) a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively. Show that ar (∆ABE) = ar (∆ACF).
Solution.
Since ∆ABE and parallelogram BCYE are on the same base BE and between the same parallels EB and AC. Therefore
ar (∆ABE) = \(\frac { 1 }{ 2 }\) ar (||gm BCYE) …(i)
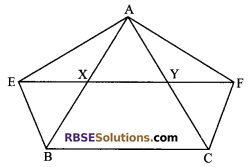
Similarly, ∆ACF and parallelogram BCFX are on the same (RBSESolutions.com) base CF and between the same parallels FC and AB. Therefore
ar (∆ACF) = \(\frac { 1 }{ 2 }\) ar (||gm BCFX) …(ii)
But parallelogram BCYE and BCFX are on the same base BC and between the same parallels BC and EF.
ar (||gm BCYE) = ar (||gm BCFX) …….. (iii)
Using relations (i), (ii) and (iii), we have
ar (∆ABE) = ar (∆ACF).
![]()
Question 2.
Diagonals AC and BD of trapezium ABCD with AB || DC intersect (RBSESolutions.com) each other at O. Prove that ar (∆AOD) = ar (∆BOC).
Solution.
Given: ABCD is a trapezium in which AB || DC and diagonals AC and BD intersect each other at O.
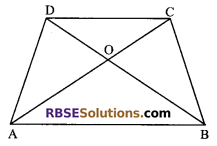
To prove: ar (∆AOD) = ar (∆BOC)
Proof: Since ∆’s ABC and ABD lie on the same base AB and between the same parallels AB and DC.
Therefore ar (∆ABC) = ar (∆ABD) …(i)
Subtracting ar (∆AOB) from both sides of (i), we get
ar (∆ABC) – ar (∆AOB) = ar (∆ABD) – ar (∆AOB)
⇒ ar (∆BOC) = ar (∆AOD)
i.e. ar (∆AOD) = ar (∆BOC)
Question 3.
Diagonals AC and BD of a quadrilateral ABCD intersect at O in (RBSESolutions.com) such a way that ar (∆AOD) = ar (∆BOC). Prove that ABCD is a trapezium.
Solution.
Given: ABCD is a quadrilateral in which AC and BD are diagonals which intersect at O, such that ar (∆AOD) = ar (∆BOC)
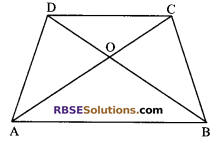
To prove: ABCD is a trapezium.
Proof: We are given that
ar (∆AOD) = ar (∆BOC) …(i)
Adding ar (∆AOB), we get on both sides
ar (∆AOD) + ar (∆AOB) = ar (∆BOC)+ ar (∆AOB)
⇒ ar (∆ABD) = ar (∆ABC)
But triangles ABD and ABC are on the same base AB and have equal in areas.
Therefore they must lie in between the same parallels, i.e. AB || DC
Hence, ABCD is a trapezium.
Question 4.
Prove that “Parallelograms on the (RBSESolutions.com) same base and between the same parallels are equal in area”.
Solution.
Given: Two parallelograms PQRS and PQMN, which have the same base PQ and which are between the same parallels lines PQ and NR.
To prove: ar (||gm PQRS) = ar (||gm PQMN)
Proof: ar (||gm PQRS) = ar (quad. PQMS) + ar (AQRM) ….(i)
Also ar (||gm PQMN) = ar (quad. PQMS) + ar (APSN) …(ii)
Now, in triangles RQM and SPN
RQ = SP (opposite sides of a ||gm)
QM = NP (opposite sides of a ||gm)
∠RQM = ∠SPN (∵ QR || SP and QM || PN)
∆RQM = ∆SPN (by SAS congruency property)
⇒ ar (∆RQM) = ar (∆SPN) …(iii)
Using relations (i), (ii) and (iii), we get
ar (||gm PQRS) = ar (||gm PQMN).
Question 5.
The side AB of a parallelogram ABCD is produced to (RBSESolutions.com) any point P. A line through A, parallel to CP meets CB produced at Q and the parallelogram PBQR is completed. Prove that ar (||gm ABCD) = ar (||gm PBQR).
Solution.
Given: The side AB of a parallelogram ABCD is produced to P. AQ || CP where Q is on CB produced. PBQR is a parallelogram.
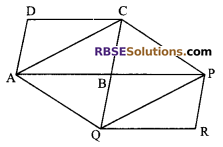
To prove: ar(||gm ABCD) = ar(||gm PBQR)
Construction: Join AC and QP
Proof: In parallelogram ABCD, AC is a diagonal
ar (||gm ABCD) = 2 ar (∆ABC) …(i)
Similarly, in (RBSESolutions.com) parallelogram PBQR, QP is a diagonal
ar (||gm PBQR) = 2 ar (∆BPQ) …(ii)
Now ∆AQC and ∆AQP are on the same base AQ and between the same parallels AQ and CP.
ar (∆AQC) = ar (∆AQP)
ar (∆AQC) – ar (AAQB) = ar (∆AQP) – ar (∆AQB)
⇒ ar (∆ABC) = ar (∆BPQ) …(iii)
From (i), (ii) and (iii), we get
ar (||gm ABCD) = ar (||gm PBQR).
![]()
Long Answer Type Questions
Question 1.
D, E and F are respectively the mid-points (RBSESolutions.com) of the sides BC, CA and AB of a ∆ABC. Show that:
(i) BDEF is a parallelogram
(ii) ar (∆DEF) = \(\frac { 1 }{ 4 }\) ar (∆ABC)
(iii) ar (BDEF) = \(\frac { 1 }{ 2 }\) ar (∆ABC)
Solution.
Given: In ∆ABC, D, E and F are mid-points
of sides BC, CA and AB respectively.
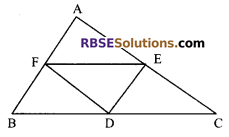
To prove:
(i) BDEF is a parallelogram
(ii) ar (∆DEF) = \(\frac { 1 }{ 4 }\) ar (∆ABC)
(iii) ar (BDEF) = \(\frac { 1 }{ 2 }\) ar (∆ABC)
Proof: (i) In ∆ABC, F is the (RBSESolutions.com) mid-point of AB and E is the mid-point of AC.
Therefore from mid-point theorem
EF || BC and EF = \(\frac { 1 }{ 2 }\) AB = BD …(i)
Similarly, DE || AB and DE = \(\frac { 1 }{ 2 }\) AB = BF … (ii)
EF || BD and EF = BD
⇒ BDEF is a parallelogram.
(ii) Here DF is diagonal of ||gm BDEF
ar (∆BDF) = ar (∆DEF) …(iii)
Similarly, ar (ADEF) = ar (∆AEF) …(iv)
and ar (∆CDE) = ar (∆DEF) …(v)
From (iii), (iv) and (v), we have
ar (∆BDF) = ar (∆AFE)
ar (∆DEF) = ar (∆CDE)
But ar (∆BDF) + ar (∆AFE) + ar (∆DEF) + ar (∆CDE) = ar (∆ABC)
⇒ 4 ar (∆DEF) = ar (∆ABC)
⇒ ar (∆DEF) = \(\frac { 1 }{ 4 }\) ar (∆ABC) …(vi)
(iii) Now, area (RBSESolutions.com) of parallelogram BDEF = ar (∆BDF) + ar (∆DEF) [∵ ar (∆BDF) ar (∆DEF)]
⇒ ar (||gm BDEF) = 2 ar(∆DEF) = 2x \(\frac { 1 }{ 4 }\) ar (∆ABC) [using relation (vi)]
= \(\frac { 1 }{ 2 }\) ar (∆ABC)
Hence, ar (||gm BDEF) = \(\frac { 1 }{ 2 }\) ar (∆ABC)
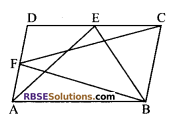
Question 2.
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
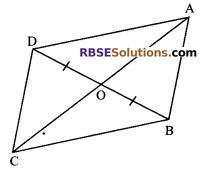
(i) ar (∆DOC) = ar (∆AOB)
(ii) ar (∆DCB) = ar (∆ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC]
Solution.
Given: ABCD is (RBSESolutions.com) a quadrilateral in which AC and BD are diagonals and they intersect each other at O such that OB = OD.
To prove:
(i) ar (∆DOC) = ar (∆AOB)
(ii) ar (∆DCB) = ar (∆ACB)
(iii) DA || CB or ABCD is a parallelogram.
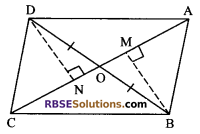
Construction: Draw DN ⊥ AC and BM ⊥ AC
Proof: (i) O is the mid-point of diagonal BD.
Therefore AO and CO will (RBSESolutions.com) be the medians of ∆ABD and ∆BCD respectively.
ar (∆AOD) = ar (∆AOB) …(i)
and ar (∆COD) = ar (∆BOC) …(ii)
Reason: Median of a triangle divides it into two triangles equal in areas.
ar (∆AOD) + ar (∆COD) = ar (∆AOB) + ar (∆BOC)
⇒ ar (∆ACD) = ar (∆ABC)
⇒ \(\frac { 1 }{ 2 }\) AC x DN = \(\frac { 1 }{ 2 }\) AC x BM
⇒ DN = BM
Now in ∆CND and ∆ABM
AB = CD (given)
DN = BM
and ∠DNC = ∠BMA = 90°
⇒ ∆CND = ∆ABM (by R.H.S. congruence rule)
⇒ ar (∆CND) = ar (∆ABM) …(iii)
Similarly, in ∆DON and ∆BOM
DN = BM
DO = OB (given)
and ∠DNO = ∠BOM = 90° (each)
∆DON = ∆BOM (by R.H.S. congruence rule)
⇒ ar (∆DON) = ar (∆BOM) …(iv)
On adding (iii) and (iv), we get
ar (∆CND) + ar (∆DON) = ar (∆ABM) + ar (∆BOM)
⇒ ar (∆DOC) = ar (∆AOB)
(ii) ar (∆DOC) = ar (∆AOB)
On Adding ar (∆BOC) to both side, we get
ar (∆DOC) + ar (∆BOC) = ar (∆AOB) + ar (∆BOC)
⇒ ar (∆DCB) = ar (∆ACB)
(iii) Since A’s DCB and ACB are on the (RBSESolutions.com) same base BC and equal areas, therefore they must lie between the same parallels
i.e. DA || CB …(v)
∆CDN = ∆ABM and ∆DNO = ∆BMO [by using relations (iii) and (iv)]
∠CDN = ∠ABM and ∠NDO = ∠MBO
On adding, we get
∠CDN + ∠NDO = ∠ABM + ∠MBO
⇒ ∠CDO = ∠ABO
But these are alternate angles. Therefore CD || BA and DA || CB.
Hence, ABCD is a parallelogram.
![]()
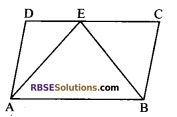
Question 3.
ABCD is a parallelogram, E and F are (RBSESolutions.com) the mid-points of BC and CD respectively.
Prove that: ar (∆AEF) = \(\frac { 3 }{ 8 }\) ar (||gm ABCD)
Solution.
Given: ABCD is a parallelogram in which E and F are the mid-points of sides BC and CD respectively.
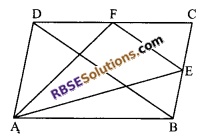
To prove: ar (∆AEF) = \(\frac { 3 }{ 8 }\) ar (||gm ABCD)
Construction: Join BD and EF.
Proof: In ∆BCD, E is the mid-point of BC and F is the mid-point of CD


![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 10 Area of Triangles and Quadrilaterals Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 10 Area of Triangles and Quadrilaterals Additional Questions, drop a comment below and we will get back to you at the earliest.