RBSE Solutions for Class 9 Maths Chapter 10 त्रिभुजों तथा चतुर्भुजों के क्षेत्रफल Ex 10.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 10 त्रिभुजों तथा चतुर्भुजों के क्षेत्रफल Exercise 10.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 10 |
| Chapter Name | त्रिभुजों तथा चतुर्भुजों के क्षेत्रफल |
| Exercise | Exercise 10.1 |
| Number of Questions Solved | 3 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 10 त्रिभुजों तथा चतुर्भुजों के क्षेत्रफल Ex 10.1
प्रश्न 1.
निम्नलिखित आकृतियों में कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के मध्य स्थित है? ऐसी स्थिति में उभयनिष्ठ आधार और समान्तर रेखायुग्म लिखिए।
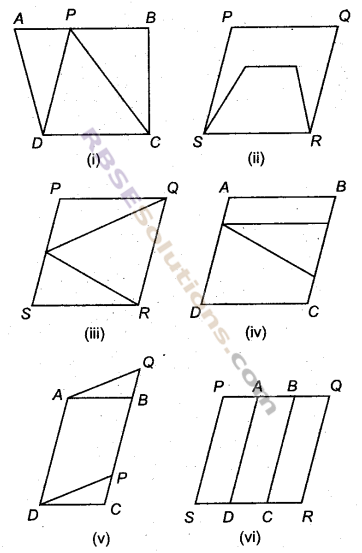
हल:
(i) त्रिभुज PCD तथा समलम्ब ABCD एक ही आधार तथा एक ही समान्तर रेखाओं के मध्य स्थित है।
उभयनिष्ठ आधार = CD, तथा समान्तर रेखायुग्म = CD तथा AB
(ii) समान्तर चतुर्भुज PQRS तथा समलम्ब चतुर्भुज का एक ही आधार SR है। परन्तु वे एक ही समान्तर रेखायुग्म के मध्य स्थित नहीं हैं।
(iii) त्रिभुज तथा समान्तर चतुर्भुज PQRS एक ही आधार(RBSESolutions.com)पर तथा एक ही समान्तर रेखाओं के मध्य स्थित हैं।
उभयनिष्ठ आधार = QR,
तथा समान्तर रेखायुग्म = QR तथा PS
(iv) त्रिभुज तथा समान्तर चतुर्भुज ABCD एक ही समान्तर रेखाओं के बीच में स्थित है परन्तु दोनों का आधार एक नहीं है।
(v) समान्तर चतुर्भुज ABCD तथा ADPQ एक ही आधार AD तथा एक ही(RBSESolutions.com)समान्तर रेखाओं के मध्य स्थित हैं।
अत: उभयनिष्ठ आधार = AD,
तथा समान्तर रेखायुग्म = AD तथा QC
(vi) समान्तर चतुर्भुज ADSP, ABCD तथा BQRC का आधार एक नहीं है तथा एक ही समान्तर रेखाओं के मध्ये स्थित है।
![]()
प्रश्न 2.
एक ही आधार एवं एक ही समान्तर रेखा युग्म के मध्य निम्न आकृतियाँ अपनी अभ्यास पुस्तिका में बनाइए-
(i) एक अधिककोण त्रिभुज और एक समलम्ब चतुर्भुज
(ii) एक समान्तर चतुर्भुज(RBSESolutions.com)और एक समद्विबाहु त्रिभुज
(iii) एक वर्ग और एक समान्तर चतुर्भुज
(iv) एक आयत और एक समचतुर्भुज ।
(v) एक समचतुर्भुज और एक समान्तर चतुर्भुज
हल:
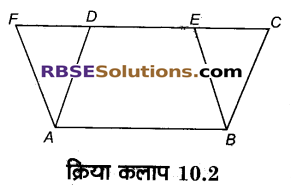
(i) अधिककोण त्रिभुज ABD तथा समलम्ब ABCD एक ही आधार AB पर तथा एक ही समान्तर रेखाओं AB तथा CD के मध्य स्थित हैं।

(ii) समद्विबाहु त्रिभुज DP PAB तथा समन्तर चतुर्भुज ABCD एक ही आधार AB पर तथा एक ही समान्तर रेखाओं AB और CD के मध्य स्थित है।
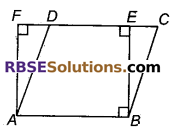
(iii) वर्ग ABEF तथा F D समान्तर चतुर्भुज ABCD एक ही आधार AB पर तथा एक ही समान्तर रेखाओं AB तथा FC के मध्य स्थित हैं।
![]()
(iv) आयत ABEF तथा समचतुर्भुज ABCD एक ही A आधार AB पर तथा एक ही समान्तर रेखाओं AB तथा CF के मध्य स्थित हैं।
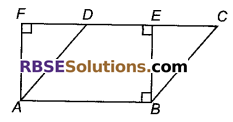
(v) समान्तर चतुर्भुज ABCD तथा समचतुर्भुज ABEF एक ही आधार AB पर तथा एक ही समान्तर रेखाओं AB और CF के मध्य स्थित हैं।
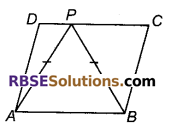
चरण 1: तीन सफेद कागजों के मध्य कार्बन रखकर कार्बन प्रति सहित एक ही समान्तर चतुर्भुज की दो प्रतियाँ बनाइए और ABCD द्वारा चारों शीर्षों को नामांकित भी कीजिए, जिसकी भुजा CD पर एक बिन्दु P इतने दबाव के(RBSESolutions.com)साथ लगाइए कि वह कार्बन प्रति पर भी आ जाए।
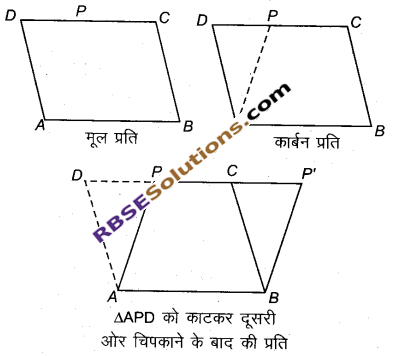
चरण 2 : (i) मूल प्रति को काटकर अपनी अभ्यास पुस्तिका के एक पृष्ठ पर चिपकाइए।
(ii) कार्बन प्रति पर अंकित P को A से मिलाने के(RBSESolutions.com)बाद बने APD को काटिए। ∆APD को कार्बन प्रति के दूसरी ओर इस प्रकार चिपकाएँ कि कटे हुए त्रिभुज की भुजा AD कटने के बाद प्राप्त समलम्ब ABCP की भुजा BC को सम्पाती करे। ध्यान रहे बिन्दु A, B पर व D,C पर रहना चाहिए।
इस प्रकार हमें दो नये समान्तर चतुर्भुज ABCD एवं ABPP प्राप्त हो रहे हैं। दोनों प्राप्त नये चतुर्भुजों को अभ्यास पुस्तिका के पृष्ठ पर चिपका दीजिए।
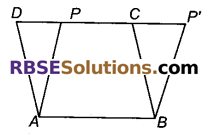
चरण 3 : दूसरे नये समान्तर ABPP को मूल प्रति पर इस प्रकार चिपकाएं कि दोनों समान्तर चतुर्भुजों की भुजा AB सम्पाती हो जाए। इस प्रकार एक नई आकृति में दो समान्तर चतुर्भुज ABCD एवं ABPP एक ही आधार व एक ही(RBSESolutions.com)समान्तर रेखाओं के मध्य बने है।
![]()
प्रश्न 3.
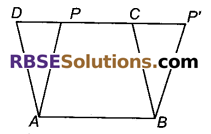
क्या आप कह सकते हैं कि समान्तर चतुर्भुज ABCD एवं ABP’P क्षेत्रफल में बराबर हैं?
हल:
चूंकि ∆APD = ∆BPC (∆APD को ही काटकर चिपकाया है)
अतः ar (APD) = ar (BP’C)
दोनों ओर ar (ABCP) जोड़ने पर
ar (APD) + ar (ABCP) = ar (ABCP)+ ar (BP’C)
या ar (ABCD) = ar (ABP’P)
अर्थात् दोनों समान्तर चतुर्भुज, जो एक(RBSESolutions.com)ही उभयनिष्ठ भुजा AB
तथा AB || DP’ (समान्तर युग्म) के मध्य बने हैं, क्षेत्रफल में बराबर हैं।
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 10 त्रिभुजों तथा चतुर्भुजों के क्षेत्रफल Ex 10.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 10 त्रिभुजों तथा चतुर्भुजों के क्षेत्रफल Exercise 10.1, drop a comment below and we will get back to you at the earliest.