RBSE Solutions for Class 9 Maths Chapter 10 Area of Triangles and Quadrilaterals Ex 10.3 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 10 Area of Triangles and Quadrilaterals Ex 10.3.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 10 |
| Chapter Name | Area of Triangles and Quadrilaterals |
| Exercise | Ex 10.3 |
| Number of Questions Solved | 15 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 10 Area of Triangles and Quadrilaterals Ex 10.3
Question 1.
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm², then ar (∆ABC) = 24 cm². Is this statement true or false. Give reason for your answer.
Solution.
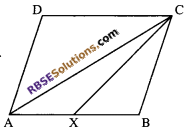
ABCD is a parallelogram and X is the mid-point of AB. Draw the diagonal AC.
We know that diagonal of (RBSESolutions.com) a parallelogram divides it into two triangles of equal areas.
So, ar (||gm ABCD) = ar (∆ADC) x 2
= 2 x 24 = 48 cm²
Since, CX is the median of ∆ABC
∴ ar (∆BCX) = \(\frac { 1 }{ 2 }\) ar (∆ABC)
= \(\frac { 1 }{ 2 }\) x 24 = 12 cm²
Now,
ar (∆XCD) = ar(||gm ABCD) – ar (∆BXC)
= 48 – 12 = 36 cm²
Hence, the given statement is false.
![]()
Question 2.
PQRS is a rectangle inscribed in a quadrant (RBSESolutions.com) of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (∆PAS) = 30 cm².
Solution.
In ∆PQR,
PR² = PQ² + RQ²
(by Pythagoras theorem)
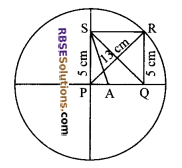
=> PQ² = PR² – RQ² = (13)² – (5)²
(given PS = 5 cm, PR = 13 cm)
=> PQ = √169-25 = √144 = 12 cm
Now, area of rectangle PQRS
= 12 x 5 = 60 cm²
Area of ∆PSQ = \(\frac { 1 }{ 2 }\) x 60 = 30 cm²
(Since, diagonal of a rectangle bisects it into two triangles of equal areas)
Now, A is any point on PQ. So, area of ∆APS depends on position of A. If A is at point Q, then area will be 30 cm².
∴ ar (∆PAS) ≤ 30 cm².
Hence proved.
Question 3.
PQRS is a parallelogram, whose area is 180 cm² and A is any point (RBSESolutions.com) on the diagonal QS. Then, the area of ∆ASR = 90 cm². This statement is true or false. Why?
Solution.
This statement is False.
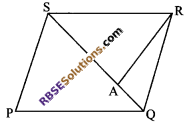
Given, area of parallelogram PQRS is 180 cm² and QS is its diagonal which divides it into two triangles of equal areas.
∴ Area of ∆PQS = 90 cm²
Now, A is any point on QS.
∴ Area of ∆ASR < Area of ∆SRQ.
Question 4.
∆ABC and ∆BDE are two equilateral triangles such (RBSESolutions.com) that D is the mid-point of BC, then
ar (∆BDE) = \(\frac { 1 }{ 4 }\) ar (∆ABC).
Solution.
Given: In a ∆ABC, AD is the median and E is mid-point of AD.
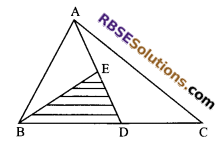
To prove: ar (∆BDE) = \(\frac { 1 }{ 4 }\) ar (∆ABC).
Proof: ∵ AD is the median of ∆ABC
∴ ar (∆ABD) = \(\frac { 1 }{ 2 }\) ar (∆ABC) …(i)
Reason: Median divides the (RBSESolutions.com) triangle into two triangles equal in area.
Also in ∆BAD, BE is median.
∴ ar (∆BED) = \(\frac { 1 }{ 2 }\) ar (∆ABD) …(ii)
Using (i) and (ii), we get
area (∆BED) = \(\frac { 1 }{ 2 }\) X \(\frac { 1 }{ 2 }\) ar (∆ABC)
Yes, the given statement is true.
Question 5.
In figure, ABCD and EFGD are (RBSESolutions.com) two parallelograms and G is the mid-point of CD, then
ar (∆DPC) = \(\frac { 1 }{ 2 }\) ar (EFGD)
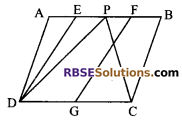
Solution.
Given: ABCD and EFGD are ||gm and G is mid-point of CD.
To prove: ar (∆DPC) = \(\frac { 1 }{ 2 }\) ar (EFGD)
Proof: ar (∆DPC) = \(\frac { 1 }{ 2 }\) ar (||gm ABCD)
(∵ ∆PDC and parallelogram ABCD are on the the same base DC and between the same parallels AB and CD)
∵ G is mid-point of DC.
∴DG = \(\frac { 1 }{ 2 }\)DC
∴ar (EFGD) = \(\frac { 1 }{ 2 }\) ar (ABCD) …(ii)
=> ar (∆DPC) = ar (EFGD)
The given statement is false.
![]()
Question 6.
In a trapezium ABCD, AB || DC and L is the (RBSESolutions.com) mid-point of BC. Through L a line PQ is drawn parallel to AD which meets DC produced at Q.
Prove that ar (ABCD) = ar (APQD).
Solution.
In ∆LPB and ∆CLQ
∠1 = ∠2
(Vertically opposite angles)
∠3 = ∠4 (alternate angles)
and BL = LC
(as L is mid-point of BC)
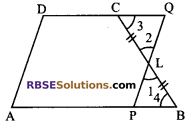
∴∆LPB ≅ ∆LQC
(by ASA congruency rule)
⇒ ar (∆LPB) + ar (∆DCLP)
⇒ ar (∆CLQ) + ar (∆DCLP)
⇒ ar (∆BCD) = ar (∆PQD)
Hence proved.
Question 7.
If the mid-point of the sides of (RBSESolutions.com) a quadrilateral are joined in order, then prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (see figure).
[Hint: Join BD and draw perpendicular from A on BD]
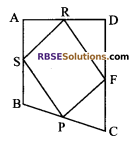
Solution.
Given: ABCD is (RBSESolutions.com) a quadrilateral and P, F, R and S are mid-points of the sides BC, CD, AD and AB respectively and PFRS is a parallelogram.
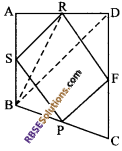
To prove:
ar (||gm PFRS) = \(\frac { 1 }{ 2 }\)ar (quad. ABCD)
Construction: Join BD and BR.
Proof: Median BR divides ∆BDA into two triangles of equal areas.
ar (∆BRA) = \(\frac { 1 }{ 2 }\) ar (∆BDA) ..(i)
Similarly, median RS divides ∆BRA into (RBSESolutions.com) two triangles of equal areas.
ar (∆ASR) = \(\frac { 1 }{ 2 }\) ar (∆BRA) …(ii)
From equation (i) and (ii), we get
ar (∆ASR) = \(\frac { 1 }{ 4 }\) ar (∆BDA) …(iii)
Similarly,
ar (∆CFP) = \(\frac { 1 }{ 4 }\) ar (∆BCD) …(iv)
On adding equations (iii) and (iv), we get
ar (∆ASR) + ar (∆CFP) = \(\frac { 1 }{ 4 }\) [ar (∆BDA) + ar (∆BCD)
ar (∆ASR) + ar (∆CFP) = \(\frac { 1 }{ 4 }\) ar (quadrilateral ABCD) …(v)
Similarly, ar (∆DRF) + ar (∆BSP) = \(\frac { 1 }{ 2 }\) ar (quadrilateral ABCD) …(vi)
On adding (v) and (vi), we get
ar (∆ASR) + ar (∆CFP) + ar (∆DRF) + ar (ABSP)
= \(\frac { 1 }{ 2 }\) ar (quadrilateral ABCD) …..(vii)
But
ar (∆ASR) + ar (∆CFP) + ar (∆DRF) + ar (∆BSP) + ar (||gm PFRS)
= ar (quadrilateral ABCD) …(viii)
On subtracting equation (vii) from equation (viii), we get
ar (||gm PFRS) = \(\frac { 1 }{ 2 }\) ar
(quadrilateral ABCD)
Hence proved.
Question 8.
A man walks 10 m towards (RBSESolutions.com) East and then he walks 30 m towards North. Find his distance from the starting point.
Solution.
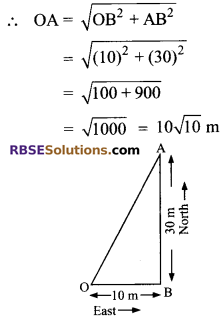
Question 9.
A ladder is placed in such a way that its foot is (RBSESolutions.com) at a distance of 7 m from the wall. If its other end reaches a window, a height of 24 m, then find the length of the ladder.
Solution.
In ∆ABC,
AC² = AB² + BC²
(Using Baudhayan theorem)
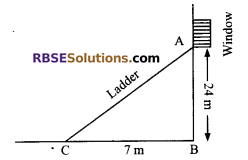
AC² = (24)² + (7)²
= 576 + 49 = 625
=> AC = √625 = 25 m
Hence, length of the ladder = 25 m.
Question 10.
Two poles stand vertically on (RBSESolutions.com) a level ground. Their height are 7 m and 12 m respectively. If the distance between their feets is 12 m. Find the distance between their tops.
Solution.
Here AB = 7 m and CD = 12 m
CP = (12 – 7) m = 5 m
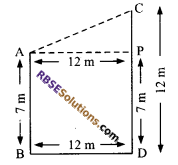
∴In right angled ∆APC
AC² = AP² + PC²
=> AC² = (12 m)² + (5 m)²
=> AC² = 144 m² + 25 m²
=> AC = √169 m
=> AC = 13 m
Hence, distance between their tops is 13 m.
![]()
Question 11.
Find the length of the altitude and area of (RBSESolutions.com) an equilateral triangle of side ‘a’
Solution.
∵ ABC is an equilateral triangle.
∴ AB = BC = CA = a
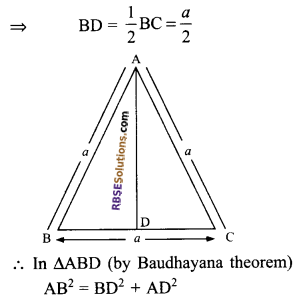

Question 12.
Find the length of the diagonal of (RBSESolutions.com) a square whose each side is of 4 m.
Solution.
Length of diagonal of a square = √2a
= √2×4
= 4√2 m
Question 13.
In an equilateral triangle ABC, AD is perpendicular to BC, prove that 3AB² = 4AD².
Solution.
∵ AD ⊥ BC(given)
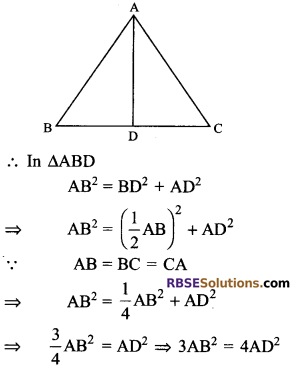
Hence proved.
Question 14.
O is a point inside (RBSESolutions.com) the rectangle ABCD. Prove that OB² + OD² = OA² + OC².
Solution.
Given: O is a point inside the rectangle ABCD.
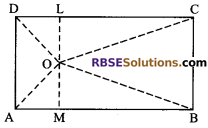
To prove: OB² + OD² = OA² + OC².
Construction: Join O, with the vertices A, B, C and D of rectangle ABCD. Now draw (RBSESolutions.com) a parallel line LM through O which meets AB and DC at M and L respectively.
Proof: In ∆OMB
OB² = OM² + MB² = OM² + CL²
(by Baudhayan theorem)
Since, ABCD is a rectangle and ML ⊥ AB
MB = CL and in ∆ODL
OD² = OL² + DL²
= OL² + AM² (∵ DL = AM)
∴ OB² + OD² = OM² + CL² + OL² + AM²
= (OM² + AM²) + (CL² + OL²)
= OA² + OC²
Hence, OB² + OD² = OA² + OC²
Hence proved.
Question 15.
In an obtuse angled triangle ABC, ∠C is an obtuse angle and AD ⊥ BC which (RBSESolutions.com) meets BC produced at D. Then prove that AB² = AC² + BC² + 2BC • CD.
Solution.
In right angled ∆ADB
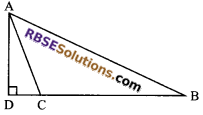
Using Baudhayan theorem
AB² = AD² + DB²
or AB² = AD² + (DC + CB)²
or AB² = AD² + DC² + BC² + 2BC • DC
or AB² = (AD² + DC²) + BC² + 2BC • CD
=> AB² = AC² + BC² + 2BC • CD
(In ∆ADC, AC² = AD² + DC²)
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 10 Area of Triangles and Quadrilaterals Ex 10.3 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 10 Area of Triangles and Quadrilaterals Ex 10.3, drop a comment below and we will get back to you at the earliest.