RBSE Solutions for Class 9 Maths Chapter 11 Area of Plane Figures Additional Questions

RBSE Solutions for Class 9 Maths Chapter 11 Area of Plane Figures Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 11 Area of Plane Figures Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 9
Subject	Maths
Chapter	Chapter 11
Chapter Name	Area of Plane Figures
Exercise	Additional Questions
Number of Questions Solved	11
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 11 Area of Plane Figures Additional Questions

Multiple Choice Questions

Question 1.
If the area of an equilateral triangle is 16√3 cm², then the (RBSESolutions.com) perimeter of the triangle is:
(A) 48 cm
(B) 24 cm
(C) 12 cm
(D) 306 cm
Solution
(B) 24 cm

Question 2.
If two sides of a right-angled triangle are 5 cm then the third side is:
(A) 13 cm
(B) 17 cm
(C) 7 cm
(D) 4 cm
Solution
(A) 13 cm

Question 3.
The area of the triangle (RBSESolutions.com) having sides 1 m, 2 m and 2 m respectively is:

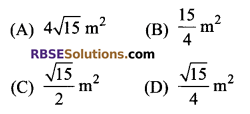
Solution
(D) \(\frac { \surd 15 }{ 4 }\) m²

Question 4.
1 Hectare is equal to:
(A) 10 arc
(B) 100 arc
(C) 1000 arc
(D) None of these
Solution
(B) 100 arc

Question 5.
Area of an equilateral triangle (RBSESolutions.com) of side 10 cm is:
(A) 100√3 cm²
(B) 50√3 cm²
(C) 25√3 cm²
(D) 10√3 cm²
Solution
(C) 25√3 cm²

Question 6.
The base and hypotenuse of a right triangle are respectively 12 cm and 13 cm long. Its area is:
(A) 25 cm²
(B) 65 cm ²
(C) 30 cm²
(D) 40 cm²
Solution
(C) 30 cm²

Question 7.
The perimeter of a triangle is 30 m. If its (RBSESolutions.com) sides are in the ratio 1 : 3 : 2, then its smallest side is:
(A) 1 cm
(B) 5 cm
(C) 10 cm
(D) 15 cm
Solution
(B) 5 cm

Question 8.
The area of an isosceles triangle is 12 sq. cm. If one of the equal sides is 5 cm, then the length of the base is:
(A) 4 cm
(B) 5 cm
(C) 6 cm
(D) 12 cm
Solution
(C) 6 cm

Question 9.
The height of an equilateral (RBSESolutions.com) triangle is 10 cm, its area is:

Solution
(D) \(\frac { 100 }{ \surd 3 }\) cm²

Question 10.
The area of a right-angled triangle is 40 times its base, then its height is:
(A) 45 cm
(B) 80 cm
(C) 60 cm
(D) None of these
Solution
(B) 80 cm

Very Short Answer Type Questions

Question 1.
The area of an equilateral triangle is 16√3 cm². Find the (RBSESolutions.com) length of each side of the triangle.
Solution.
Area of an equilateral triangle = \(\frac { \surd 3 }{ 4 }\) (side)²
⇒ 16√3 = \(\frac { \surd 3 }{ 4 }\) (side)²
⇒ (side)² = 64
⇒ side = √64 = 8 cm

Question 2.
Find the altitude of a triangular region whose base is 40 m and area is 560 m².
Solution.
Area of triangular region = \(\frac { 1 }{ 2 }\) x base x altitude
560 m² = \(\frac { 1 }{ 2 }\) x 40 m x altitude
⇒ 560 m² = 20 m x altitude
⇒ altitude = 28 m

Question 3.
The edges of a triangular board are 6 cm, 8 cm and 10 cm respectively. Find the (RBSESolutions.com) cost of painting at the rate of ₹ 9 per m².
Solution.
Semi-perimeter of a triangular board = \(\frac { 6+8+10 }{ 2 }\) = 12 cm
Area of triangular board = \(\sqrt { 12(12-6)(12-8)(12-10) } \)
= \(\sqrt { 12\times 6\times 4\times 2 } \)
= 24 cm²
Cost of painting 1 cm² is ₹ 9
Cost of painting 24 cm² is 24 x 9 = ₹ 216.

Question 4.
Find the percentage increase in the area (RBSESolutions.com) of an equilateral triangle if its every side is doubled.
Solution.
Let each side of an equilateral triangle be x, then its area = \(\frac { \surd 3 }{ 4 }\) x²
Now, when the side is doubled i.e. 2x.

Question 5.
Two sides of a triangular field are 85 m and 154 m and (RBSESolutions.com) its perimeter is 324 m. Find the area of the field.
Solution.
Perimeter = 324 m
⇒ Semi-perimeter (s) = 162 m
85 + 154 + third side = 324 m
⇒ third side = 324 m – 239 m = 85 m
Area of triangular field

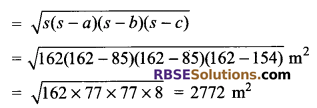
Question 6.
Find the area of (RBSESolutions.com) an equilateral triangle of side 4√3 cm.
Solution.
The side of an equilateral triangle = 4√3 cm
Area of an equilateral triangle

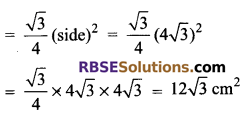
Question 7.
If the area of a square with side a is equal to the area (RBSESolutions.com) of a triangle with base a, then find the altitude of the triangle.
Solution.
Area of a square with side a = a² sq. units
Area of a triangle with base a = \(\frac { 1 }{ 2 }\) x a x h sq. units
According to question,
Area of square = Area of triangle
a² = \(\frac { 1 }{ 2 }\) x a x h
⇒ 2a² = ah
⇒ h = 2a
Hence, altitude of the triangle is 2a.

Question 8.
The perimeter of a right-angled triangle is 60 cm. Its (RBSESolutions.com) hypotenuse is 26 cm. Find the area of the triangle.
Solution.
Let base and height of a right angled triangle be b and h cm respectively
b + h + 26 = 60
⇒ b + h = 34
⇒ (b + h)² = (34)²
Also b² + h² = (26)² …(ii)
Subtracting (ii) from (i), we get
(b + h)² – (b² + h²) = (34)² – (26)²
⇒ b² + h² + 2bh – b² – h² = (34 – 26)(34 + 26)
⇒ 2bh = 8 x 60
⇒ bh = 240
⇒ Area = \(\frac { 1 }{ 2 }\) x b x h = \(\frac { 1 }{ 2 }\) x 240 = 120
Hence, area =120 cm².

Question 9.
Using Heron’s formula, find the area of (RBSESolutions.com) an equilateral triangle the length of whose one side is ‘x’.
Solution.
The semi perimeter (s) = \(\frac { x+x+x }{ 2 }\) = \(\frac { 3x }{ 2 }\)
Area of the triangle

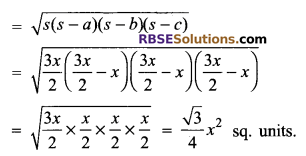
Question 10.
An isosceles right triangle has (RBSESolutions.com) an area of 200 cm². What is the length of its hypotenuse?
Solution.
Suppose ABC be an isosceles right triangle in which AB = BC = a

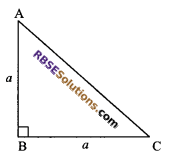
Area = \(\frac { 1 }{ 2 }\) x base x altitude
200 = \(\frac { 1 }{ 2 }\) x a x a
200 = \(\frac { 1 }{ 2 }\) x a2
⇒ a² = 2 x 200
⇒ a² = 400
⇒ a = 20 cm
i.e. AB = BC = 20 cm
Hypotenuse AC

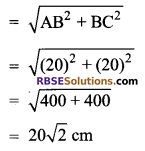
Short Answer Type Questions

Question 1.
Find the area of a triangular field, the length (RBSESolutions.com) of whose sides are 275 m, 660 m and 715 m. What is the cost of cultivating the field at the rate of ₹ 200 per hectare?
Solution.
Suppose sides of a triangular field are
a = 275 m, b = 660 m and c = 715 m

Question 2.
Find the area of the triangle ABC whose (RBSESolutions.com) dimensions are shown in the figure.

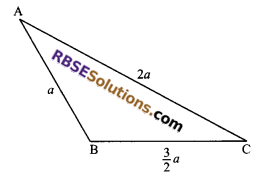
Solution.

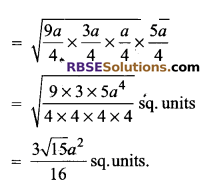
Question 3.
The area of a triangle is 30 cm². Find the base (RBSESolutions.com) if the altitude exceeds the base by 7 cm.
Solution.
Let base QR = x cm
altitude (PS) = (x + 7) cm

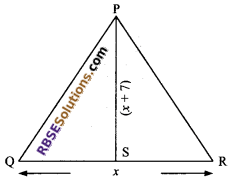
Now, area of ΔPQR = \(\frac { 1 }{ 2 }\) x base x altitude
30 = \(\frac { 1 }{ 2 }\) x QR x PS
= \(\frac { 1 }{ 2 }\) × x × (x + 7)
⇒ 60 = x² + 7x
⇒ x² + 7x – 60 = 0
⇒ x² + 12x – 5x – 60 = 0
⇒ x (x + 12) – 5 (x + 12) = 0
⇒ (x + 12)(x – 5) = 0
⇒ x = 5 or x = -12
⇒ x = -12 is not admissible
⇒ x = 5 cm
base (x) = 5 cm
and corresponding altitude = x + 7 = 5 + 7 = 12 cm.

Question 4.
The difference between the sides at right angles in (RBSESolutions.com) a right-angled triangle is 14 cm. The area of the triangle is 120 cm². Calculate the perimeter of the triangle.
Solution.
Suppose the sides containing right angle be x and (x – 14) cm
Area of right angled triangle = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) × x (x – 14) cm²
area = 120 cm²
⇒ 120 = \(\frac { 1 }{ 2 }\) x (x² – 14x)
⇒ x² – 14x – 240 = 0
⇒ x² – 24x + 10x – 240 = 0
⇒ x(x – 24) + 10(x – 24) = 0
⇒ (x – 24)(x + 10) = 0
either x – 24 = 0
⇒ x = 24
or x + 10 = 0
⇒ x = -10 (neglecting)
x = 24 cm (one side)
and another side = (x – 24) = (24 – 14) = 10 cm
Hypotenuse = √(24² + 10²) = √(576 + 100) = √676 = 26 cm
Perimeter of the triangle = 24 + 10 + 26 = 60 cm

Question 5.
A right triangle has the hypotenuse of length q cm and (RBSESolutions.com) one side of length p cm. If q – p = 2 cm, express the length of the third side of the right triangle in terms of q.
Solution.
Let length of the third side of the right triangle be x.
x² + p² = q²
⇒ x² = q2 – p²
⇒ x² = (q + p)(q – p) [∵ q – p = 2]
⇒ x² = (q + q – 2) (2)
⇒ x² = (2q – 2) x 2
⇒ x = √(4q – 4)
⇒ x = 2√(q – 1)
Hence, length of the third side of right triangle is 2√(q – 1)

Question 6.
If each side of an equilateral triangle is increased by 2 cm, then (RBSESolutions.com) its area is increased by 3√3 cm². Find the length of each side and its area.
Solution.
Suppose side of an equilateral triangle be ‘a’, then

Question 7.
Prove that the area of a triangle having (RBSESolutions.com) sides 8 m, 10 m and 12 m is 15√7 m².
Solution.
The sides of a triangle are 8 m, 10 m and 12 m respectively.
Let it be a = 8 m, b = 10 m and c = 12 m

Long Answer Type Questions

Question 1.
Find the area of (RBSESolutions.com) a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution.
Here, we are given sides of a quadrilateral ABCD as
AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Here, we see that AB² + BC² = AC²
i e. (3)² + (4)² = (5)²
Hence, ∆ABC is right angled at B

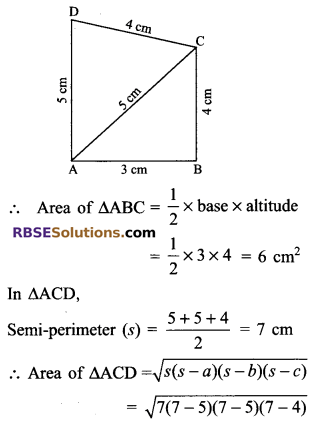
= √(7 x 2 x 2 x 3)
= 2√21 cm²
Hence, area of quadrilateral ABCD = ar (∆ABC) + ar (∆ACD) = (6 + 2√21) cm²

Question 2.
A floral design on a floor is made up of 16 tiles which (RBSESolutions.com) are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see figure). Find the cost of polishing the tiles at a rate of 50 paise per cm².

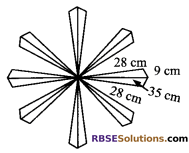
Solution.
The sides of a triangular tile in floral design are 9 cm, 28 cm and 35 cm respectively.
Semi-perimeter of triangular tile (s) = \(\frac { 9+28+35 }{ 2 }\) = \(\frac { 72 }{ 2 }\) = 36 cm
Area of a triangular tile by using Heron’s formula

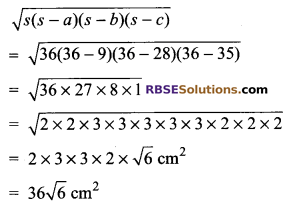
Total area of such 16 tiles (RBSESolutions.com) in a floral design
= 16 x 36√6
= 576√6
= 576 x 2.45 cm² [√6 = 2.45 approximate]
= 1411.20 cm² approximate
Cost of polishing the tile = 50 paise/cm²
Cost of polishing the 1411.20 cm² = ₹ 1411.20 x \(\frac { 1 }{ 2 }\) = ₹ 705.60.

Question 3.
A field is in the shape of a trapezium whose parallel (RBSESolutions.com) sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution.
PQRS is the given trapezium in which PQ || SR
Through R draw RM || SP

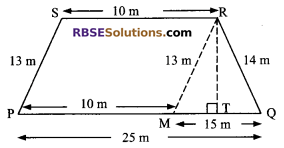
Now, PMRS become a parallelogram
PS = RM = 13 m
PM = SR = 10 m
⇒ MQ = PQ – PM = 25 m – 10 m = 15 m
Now for finding the area of the field which is trapezium in shape, we (RBSESolutions.com) first find the area of the ΔRMQ and then the height of the triangular field RMQ.
Semi-perimeter of ΔRMQ


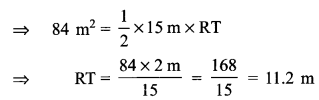
Area of parallelogram PMRS = base x altitude = 10 m x 11.2 m = 112 m²
Area of trapezium PQRS = area (||gm PMRS) + area (ΔRMQ) = 112 m² + 84 m² = 196 m²

Question 4.
A Rangoli design which is triangular in shape is made (RBSESolutions.com) on the floor, with four different colours red, pink, green and yellow (as shown in the figure).

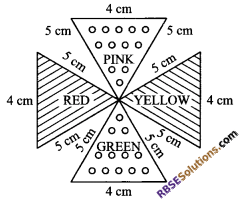
Solution.
Since, the Rangoli design is made of four similar triangles (RBSESolutions.com) with sides 5 cm, 5 cm and 4 cm respectively.

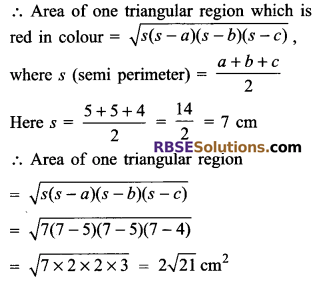
Similarly, other triangular regions: green, yellow and pink are same in area i.e. = 2√21 cm².
Hence, total triangular areas used in the Rangoli = 4 x 2√21 cm² = 8√21 cm².

Question 5.
Calculate the area of the shaded portion (RBSESolutions.com) of the triangle as shown in the figure.

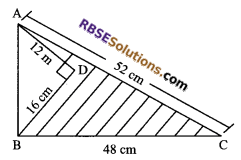
Solution.
In right angled triangle ABD
AB² = AD² + BD²
⇒ AB² = (12)² + (16)²
⇒ AB² = 144 + 256
⇒ AB² = 400 cm²
⇒ AB = √400 cm²
⇒ AB = 20 cm
Now in ΔABC, a = 48 cm, b = 52 cm, c = 20 cm.

Thus, area of shaded portion (RBSESolutions.com) of the triangle = (480 – 96) cm² = 384 cm²

We hope the given RBSE Solutions for Class 9 Maths Chapter 11 Area of Plane Figures Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 11 Area of Plane Figures Additional Questions, drop a comment below and we will get back to you at the earliest.