RBSE Solutions for Class 9 Maths Chapter 12 Surface Area and Volume of Cube and Cuboid Ex 12.2 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 12 Surface Area and Volume of Cube and Cuboid Exercise 12.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 12 |
| Chapter Name | Surface Area and Volume of Cube and Cuboid |
| Exercise | Ex 12.2 |
| Number of Questions Solved | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 12 Surface Area and Volume of Cube and Cuboid Ex 12.2
Question 1.
The dimension of a match box is 3 cm x 2 cm x 1 cm. Find (RBSESolutions.com) the volume of such 12 packets.
Solution.
Length of a match box (l) = 3 cm, breadth (b) = 2 cm and height (h) = 1 cm
Volume of one match box = l x b x h = 3 cm x 2 cm x 1 cm = 6 cm3
Volume of such 12 boxes = 6 x 12 cm3 = 72 cm3
![]()
Question 2.
The perimeter of one face of a cube is 24 cm. Find the volume of the cube.
Solution.
Let the one side of a cube be l
Perimeter = 4l
⇒ 4l = 24
⇒ l = 6 cm
Thus one side of a cube = (side)3 = l3
Volume = (6)3 = 6 x 6 x 6 = 216 cm3
Question 3.
Three cubes of metal whose edges are 3 cm, 4 cm and 5 cm respectively are (RBSESolutions.com) melted and recast into a single cube. Find the edge of this new cube.
Solution.
Let x be the edge of new cube, then
According to problem
volume of the new cube = sum of the volume of three cubes
⇒ x3 = (3)3 + (4)3 + (5)3
⇒ x3 = 27 + 64 + 125
⇒ x3 = 216
⇒ x = 6 cm
Hence, edge of the new cube is 6 cm long.
Question 4.
The length and breadth of a water tank are 2.5 m and 2 m respectively. It (RBSESolutions.com) can hold 1500 litres of water. Find the depth of water tank.
Solution.
Length of a water tank = 2.5 m
Breadth = 2 m
Suppose height/depth of water tank be h m
Volume/capacity = 1500 litres
1 m3 = 1000 litres
Volume = \(\frac { 1500 }{ 1000 }\) = 1.5 m3
According to problem,
l x b x h = Volume
2.5 x 2 x h = 1.5
⇒ h = \(\frac { 1.5 }{ 5 }\) = 0.3 m i.e. 30 cm
Question 5.
The length, breadth and height of a wall are 4 m, 15 cm and 3 m respectively. How (RBSESolutions.com) many bricks of size 20 cm x 10 cm x 8 cm will be required to make it? If the cost of bricks is Rs. 120 per thousand, then find the total cost of bricks.
Solution.
Length of wall = l1 = 4 m = 400 cm
Breadth of wall = b1 = 15 cm
Height of wall = h1 = 3 m = 300 cm
Length of bricks = 20 cm (l2)
Breadth of bricks = 10 cm (b2)
Height of bricks = 8 cm (h2)
Number of bricks used
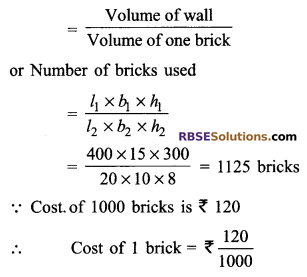
Cost of 1125 bricks = \(\frac { 120×1125 }{ 1000 }\) = Rs. 135
Thus, total number of bricks is 1125 and total cost of bricks Rs. 135.
Question 6.
A village has a water tank of dimension 20 m x 15 m x 6 m. How (RBSESolutions.com) many litres of water it can hold. If per day consumption of water is 1000 litres. For how many days will the water of this tank last?
Solution.
Quantity of water required per day = 1000 litres.
Length, breadth and height of a tank are 20 m, 15 m and 6 m respectively.
Capacity of tank = 20m x 15m x 6m = 1800 m3
1 m3 = 1000 litres
1800 m3 = 1800000 litres
Required number of days for which the water of the tank will last
= \(\frac { 1800000 }{ 1000 }\) = 1800 days
Thus, water tank can serve for 1800 days.
![]()
Question 7.
A wall is 8 m long, 4 m high and 35 cm thick. There is (RBSESolutions.com) one door of size 2 m x 1 m and two windows of size 1.20 m x 1 m. Find the cost of construction at the rate Rs. 1500 per cubic metres.
Solution.
Length of the wall = 8 metres
Thickness of the wall = 35 cm = \(\frac { 35 }{ 100 }\) m
Height of the wall = 4 metres
Volume of wall = 8 x \(\frac { 35 }{ 100 }\) x 4 = 11.2 cubic metres
and space occupied by 1 door
= 2 x 1 x \(\frac { 35 }{ 100 }\)
= \(\frac { 70 }{ 100 }\) cubic metres = 0.70 m3
Space occupied by two windows = 2 x 1.2 x 1 x \(\frac { 35 }{ 100 }\)
= \(\frac { 21 }{ 25 }\) cubic metres = 0.84 m3
The remaining volume of the wall = 11.2 – (0.70 + 0.84) = 11.2 – 1.54 = 9.66 cubic metres
Cost of construction of 1 cubic metre of wall is Rs. 1500
Cost of construction of 9.66 cubic metres of wall = 9.66 x 1500 = Rs. 14,490.
Question 8.
How many bricks of size 25 cm x 15 cm x 6 cm will be required for (RBSESolutions.com) a wall 5 m long, 2 m high and 50 cm thick, while 10% of space occupied by cement?
Solution.
Length of the wall = 5 m
Breadth of the wall = 2 m
Thickness of the wall = 50 cm = 0.50 m
Volume of wall = l x b x h cubic unit = 5 x 2 x 0.50 = 5 cubic metres
Space occupied by cement = 10% of 5 = 0.5 cubic metre
Actual space required for bricks = 5 – 0.5 = 4.5 cubic metres
Volume of 1 brick = 0.25 m x 0.15 m x 0.06 m = 0.002250 cubic metre
Total number of bricks
= \(\frac { 4.5 }{ 0.002250 }\)
= \(\frac { 4.5×1000000 }{ 2250 }\)
= 2000 bricks
Question 9.
A field is 150 metres long and 100 metres wide. If the pit in (RBSESolutions.com) the pond is 200 metres long and 50 metres wide is dug to a depth of 0.75 m and the earth is spread uniformly in the field. By how much the level of field is raised?
Solution.
Dimension of the field are 150 m and 100 m respectively.
i.e. length of the field = 150 m
and breadth of the field = 100 m
Now volume of the earth taken out from the pit = l x b x h = 200 x 50 x 0.75 = 7500 cubic metres
Due to 7500 cubic metre of earth, suppose the level of field be raised by h metres.
Volume of the field = Volume of earth taken out from the pit
⇒ 150 x 100 x h = 7500
⇒ h = \(\frac { 7500 }{ 150×100 }\) = \(\frac { 1 }{ 2 }\) m = 0.50 m
Hence, level of the field be raised by 50 cm.
Question 10.
A closed box is made of wood 2.5 cm thick. Its (RBSESolutions.com) external dimension are 1.25 m long, 0.80 m wide and 0.55 m high. If 1 cubic metre of water weighs 250 kg, find the weight of the box.
Solution.
Outer length of the box (L) = 1.25 m = 125 cm
Outer breadth of box (B) = 0.80 m = 80 cm
Outer height of box (H) = 0.55 m = 55 cm
Thickness of the wood = 2.5 cm
Inner length of the box = 125 – 2 x 2.5 = 120 cm
Inner breadth of the box = 80 – 2 x 2.5 = 75 cm
Inner height (RBSESolutions.com) of the box = 55 – 2 x 2.5 = 50 cm
Outer volume = l x b x h = 125 x 80 x 55 = 550000 cm3
Inner volume = l x b x h = 120 x 75 x 50 = 450000 cm3
Volume of wood = outer volume – inner volume = 550000 – 450000 = 100000 cubic cm
= \(\frac { 1 }{ 10 }\) cubic m
Weight of 1 cubic metre of wood is 250 kg
Weight of \(\frac { 1 }{ 10 }\) cubic metre of wood is \(\frac { 1 }{ 10 }\) x 250 = 25 kg
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 12 Surface Area and Volume of Cube and Cuboid Ex 12.2 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 12 Surface Area and Volume of Cube and Cuboid Exercise 12.2, drop a comment below and we will get back to you at the earliest.