RBSE Solutions for Class 9 Maths Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 12 |
| Chapter Name | Surface Area and Volume of Cube and Cuboid |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 14 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise
Multiple Choice Questions
Question 1.
The volume of (RBSESolutions.com) a cube is 125 cubic metres, its side is:
(A) 7 m
(B) 6 m
(C) 5 m
(D) 2 m
Solution.
(C) 5 m
Question 2.
The volume of a cube is 1331 cubic centimetre, then it surface area is:
(A) 762 sq. cm
(B) 726 sq. cm
(C) 426 sq. cm
(D) 468 sq. cm
Solution.
(B) 726 sq. cm
![]()
Question 3.
The length, breadth and height of (RBSESolutions.com) a cuboid are 4 m, 3 m and 2 m respectively, then surface area of cuboid:
(A) 25 sq. m
(B) 26 sq. m
(C) 52 sq. m
(D) 62 sq. m
Solution.
(C) 52 sq. m
Question 4.
The diagonal of a cuboid having dimension 8mx7mx6mis:
(A) 12.2 m
(B) 12.02 m
(C) 14.2 m
(D) 14.02 m
Solution.
(A) 12.2 m
Question 5.
The edge of (RBSESolutions.com) a cube is 5 cm, its diagonal
will be:
(A) 4√3cm
(B) 2√3 cm
(C) 5√3 cm
(D) 5 cm
Solution.
(C) 5√3 cm
Question 6.
The volume of cuboid is 400 cubic centimetre, and area of its (RBSESolutions.com) base is 80 sq. cm, then its height is:
(A) 7 cm
(B) 6 cm
(C) 4 cm
(D) 5 cm
Solution.
(D) 5 cm
Question 7.
A cuboid measuring 15 cm x 12 cm x 6 cm is melted. How many (RBSESolutions.com) new cubes of sides 3 cm can be made?
Solution.
Required number of new cubes
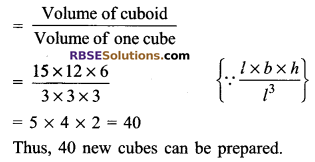
Question 8.
Two cubical dice having edge 2 cm are (RBSESolutions.com) joined end to end. Find the total surface area of the solid so formed.
Solution.
Length of the solid = 2 + 2 = 4 cm
Breadth = 2 cm
Height = 2 cm
Surface area = 2(lb + bh + hl)
= 2(4 x 2 + 2 x 2 + 2 x 4)
= 2(8 + 4 + 8)
= 2 x 20
= 40 cm
![]()
Question 9.
An empty tank is 4 m long and 3 m wide. How many cubic metre of (RBSESolutions.com) water must be filled in .it so that depth of water become 2 m?
Solution.
Length = 4 m, Breadth = 3 m and depth = 2 m
Volume of empty tank = l x b x h = (4 x 3 x 2) m3 = 24 m3
Hence, 24 m3 of water must be filled in the empty tank so that depth of water in the tank becomes 2 m.
Question 10.
A cubical vessel contains 8 litres of water. Find the total surface area of the vessel.
Solution.
Here, volume of vessel = 8 litres
But 1 litre = 1000 cm3
8 litres = 8000 cm3
Let the side of the cubical vessel be l, therefore we can write
Volume = l3
⇒ l3 = 8000
⇒ l3 = (20)3
⇒ l = 20 cm
Now, total surface area is 6l2
Area = 6 x (20)2 = 6 x 400 = 2400
Hence, total surface area = 2400 cm3
Question 11.
A godown measures 60 m x 25 m x 10 m. Find the maximum number (RBSESolutions.com) of wooden crates each measuring 1.5 m x 1.25 m x 0.5 m that can be stored in the godown.
Solution.
We have,
Length of godown = 60 m
Breadth = 25 m and height = 10 m
Volume/capacity of the godown = (60 x 25 x 10) m3
Volume of one wooden crate = (1.5 x 1.25 x 0.5) m3
Required number of wooden crates
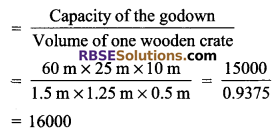
Hence, maximum 16000 crates can be stored in the godown.
Question 12.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much (RBSESolutions.com) water will fall into the sea in a minute?
Solution.
Water flowed in one minute = \(\frac { 2×1000 }{ 60 }\) = \(\frac { 100 }{ 3 }\) m
Volume of water fell into the sea in one minute
= \(\frac { 100 }{ 3 }\) x 40 x 3 = 4000 m3
Question 13.
The dimension of rectangular parallelopiped are in the ratio 6 : 5 : 4 and its total surface area is 33300 square metres. Find its volume.
Solution.
Let length, breadth and height of a cuboid are 6x, 5x and 4x respectively.
Its total surface area
= 2(lb + bh + hl)
= 2(6x × 5x + 5x × 4x + 4x × 6x)
= 2(30 x 2 + 20 x 2 + 24 x 2)
= 2 x 74 x 2
= 148 x 2
But it is given that total (RBSESolutions.com) surface area = 333000 sq.m
i.e. 148 x 2 = 33300
⇒ x2 = \(\frac { 33300 }{ 148 }\)
⇒ x2 = 225 m2
⇒ x = √225
⇒ x = 15 m
Dimensions of cuboid are
6x = 6 × 15 = 90 m
5x = 5 × 15 = 75 m
and 4x = 4 × 15 = 60 m
Volume of cuboid = 90 × 75 × 60 cubic metres = 405000 cubic metres.
![]()
Question 14.
A field is 20 metres long and 15 metres wide. A pit (outside the field) 10 metres long and 6 metres wide is due to a depth of 5 m and the earth is spread uniformly in the field. By (RBSESolutions.com) how much the level of field is raised?
Solution.
Dimension of the field are 20 m and 15 m respectively
i.e. length of the field = 20 m
and breadth of the field = 15 m
Now volume of the earth taken out from the pit = l × b × h = 10 × 6 × 5 = 300 cubic metres
Due to 300 cubic metre of earth, suppose the level of field be raised by h metres.
Volume of the field = Volume of earth taken out from the pit
⇒ 20 x 15 x h = 300
⇒ h = \(\frac { 300 }{ 300 }\) = 1 m
Hence, level of the field be raised by 1 m.
We hope the given RBSE Solutions for Class 9 Maths Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 12 Surface Area and Volume of Cube and Cuboid Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.