RBSE Solutions for Class 9 Maths Chapter 13 Angles and their Measurement Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 13 Angles and their Measurement Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 13 |
| Chapter Name | Angles and their Measurement |
| Exercise | Additional Questions |
| Number of Questions Solved | 26 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 13 Angles and their Measurement Additional Questions
Multiple Choice Questions
Question 1.
120° in radians is equal to:
(A) 3π
(B) \(\frac { 3\pi }{ 2 }\)
(C) \(\frac { 2\pi }{ 3 }\)
(D) \(\frac { \pi }{ 2 }\)
Question 2.
In the given figure, O is the centre (RBSESolutions.com) of the circle. Then (∠BAD + ∠BCD) is equal to:
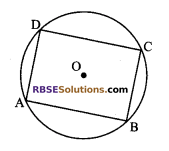
(A) 2π radian
(B) \(\frac { \pi }{ 2 }\) radian
(C) \(\frac { \pi }{ 4 }\) radian
(D) π radian
![]()
Question 3.
The value of \(\frac { 5 }{ 16 }\) right angles in sexagesimal system (RBSESolutions.com) is equal to
(A) 28° 30′ 7″
(B) 27° 5′ 26″
(C) 28° 7′ 30″
(D) 29° 3′ 27″
Question 4.
How many right angles is equal to 56° 15′?
(A) \(\frac { 8 }{ 5 }\) right angles
(B) \(\frac { 5 }{ 8 }\) right angles
(C) \(\frac { 3 }{ 5 }\) right angles
(D) \(\frac { 5 }{ 4 }\) right angles
Question 5.
In which quadrant will the revolving line lie when it traces (RBSESolutions.com) an angle \(\frac { 13\pi }{ 6 }\)?
(A) 1st quadrant
(B) 2nd quadrant
(C) 3rd quadrant
(D) 4th quadrant
Question 6.
1 radian is equal to:
(A) 180g
(B) 200g
(C) 100g
(D) None of these
Question 7.
In which quadrant, the angle (RBSESolutions.com) whose measure is – 400° will lie?
(A) First quadrant
(B) Second quadrant
(C) Third quadrant
(D) Fourth quadrant
Question 8.
The time is taken by the hour hand of (RBSESolutions.com) a clock in tracing an angle of \(\frac { \pi }{ 2 }\) radian is?
(A) 1 hour
(B) 3 hours
(C) 4 hours
(D) 6 hours
Question 9.
The value of each angle of an equilateral triangle in circular system is:
(A) \(\frac { \pi }{ 2 }\) radian
(B) \(\frac { \pi }{ 3 }\) radian
(C) \(\frac { 2\pi }{ 3 }\) radian
(D) π radian
Question 10.
Each exterior angle (RBSESolutions.com) of regular octagon is:
(A) \(\frac { \pi }{ 3 }\) radian
(B) \(\frac { \pi }{ 6 }\) radian
(C) \(\frac { \pi }{ 8 }\) radian
(D) \(\frac { \pi }{ 4 }\) radian
Answers
1. C
2. D
3. C
4. B
5. A
6. B
7. D
8. B
9. B
10. D
![]()
Very Short Answer Type Questions
Question 1.
Find the magnitude of (RBSESolutions.com) an interior angle of a regular hexagon
(i) in degree
(ii) in radians
Solution.
(i) Interior angle of a regular hexagon in degree
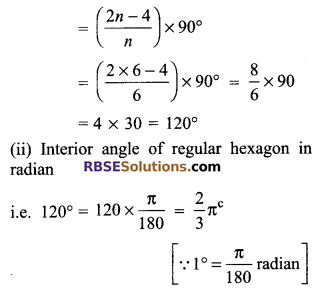
Question 2.
In which quadrant will the revolving ray lie when (RBSESolutions.com) it makes the following angles.
(i) 280°
(ii) 390°
(iii) – 400°
(iv) – 1120°
Solution.
(i) 280° = 3 right angles + 10°
Hence, the position of the revolving ray will be the fourth quadrant.
(ii) 390° = 4 right angles + 30°
Hence, the position of the revolving ray will be in the first quadrant.
(iii) – 400° = – 4 right angles – 40°
Hence, the position of the revolving ray will be in the fourth quadrant.
(iv) – 1120° = -3 x 4 right angles – 40°
Therefore, the position of the revolving ray will be in the fourth quadrant.
Question 3.
What is the measure of the angle traced (RBSESolutions.com) out by the hour hand of a clock from 9 a.m. to 3 p.m?
Solution.
The measurement of the angle traced out by the hour hand of a clock from 9 a.m. to 3 p.m. = 2 right angles = 180°
Question 4.
In which quadrant will the minute hand of a clock lie when the time in the clock is 12 : 25?
Solution.
The minute hand of a clock will lie in fourth quadrant when the time in the clock is 12 : 25.
Question 5.
Find out whether the angle XOP is positive or negative angle (RBSESolutions.com) as marked in the following figures.
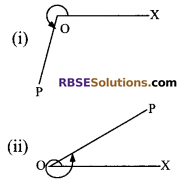
Solution.
(i) Positive
(ii) Negative
![]()
Question 6.
Convert \(\frac { \pi }{ 12 }\) radians (RBSESolutions.com) into degree (sexagesimal system).
Solution.
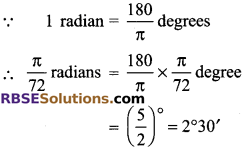
Short Answer Type Questions
Question 1.
Express the following angles (RBSESolutions.com) in degree, minutes and seconds.
(i) \(\frac { \pi }{ 8 }\) radians
(ii) \(\frac { 3\pi }{ 7 }\) radians
Solution.

Question 2.
Find the length of the arc of (RBSESolutions.com) a circle of radius 5 cm subtending a central angle measuring 15°.
Solution.

Question 3.
Express the following degrees (RBSESolutions.com) into grades (i.e., sexagesimal system to centesimal system)
(i) 63°
(ii) 108°
Solution.
(i) We know that to change degree into grades, add one-ninth into degrees.
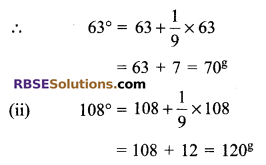
![]()
Question 4.
The vertex angle of an isosceles triangle is 40°. Find the (RBSESolutions.com) angles of the triangle in radians (i.e. in circular system).
Solution.
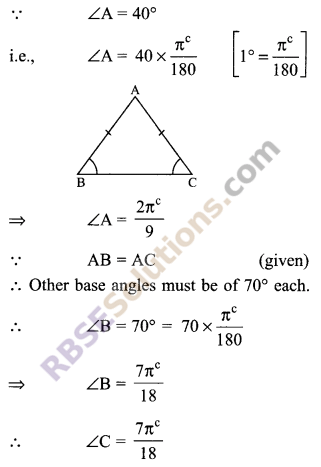
Question 5.
Find the angles in degrees traced out (RBSESolutions.com) by the big and small hands of a clock in 10 minutes.
Solution.
As we know that
the minute hand traces 4 right angles in 1 hour
Angle traced out in 60 minutes = 4 right angles = 4 x 90° = 360°
Angle traced out in 10 minutes = \(\frac { 360 }{ 60 }\) x 10 = 60°
Also, the small hand of a clock traces 4 right angles in 12 hours.
Angle traced out in 12 hours = 4 right angles
Angle traced out in 1 hour = \(\frac { 360 }{ 12 }\) = 30°
i.e. in 60 minutes, angle is traced out of 30°
In 1 minute, angle is traced out of \(\frac { 30 }{ 60 }\)
In 10 minutes, angle is traced out of = \(\frac { 30 }{ 60 }\) x 10 = 5°.
Hence, the angle in degree traced out by the big hand = 60°
and the angle traced out by the small hand = 5°.
Question 6.
Write the measurement of exterior (RBSESolutions.com) and interior angles of regular pentagon
(i) in degrees
(ii) in radian
Solution.

Question 7.
Express 104°30′ in radians.
Solution.
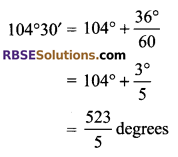

![]()
Question 8.
Find the angle subtended (RBSESolutions.com) at the centre by the circumference of the circle.
Solution.
If r be the radius of the circle, then circumference of the circle = 2πr
Also we know that:
1 radian is the measure of an angle subtended at the centre of a circle of radius r by an arc of length r.
i.e. the angle subtended at the centre by an arc of length r = 1 radian
Angle subtended at the centre by an arc of unit length = \(\frac { 1 }{ r }\) radian
The angle subtended at the centre by an arc of length 2πr = \(\frac { 1 }{ r }\) x 2πr = 2π radians.
Thus, the angle subtended at the centre of circle by the circumference = 2π.
Question 9.
The difference between two acute angles (RBSESolutions.com) of a right-angled triangle is \(\frac { \pi }{ 9 }\). Find the angles in degrees.
Solution.
π radians = 180°
\(\frac { \pi }{ 9 }\) radian = \(\frac { 180 }{ \pi } \times \frac { \pi }{ 9 }\) = 20°
Let the two acute angles of the right¬angled triangle be x and y (x > y).
Then x + y = 90° …(i)
and x – y = 20° …(ii)
Solving (i) and (ii) we get
2x = 110°
⇒ x = 55°
55° + y = 90° ⇒ y = 35°
Hence, two angles are 55° and 35° respectively.
Question 10.
Find the angle subtended at the centre of (RBSESolutions.com) a circle of radius 3 cm by an arc of length 1 cm.
Solution.
The number of radians in the angle

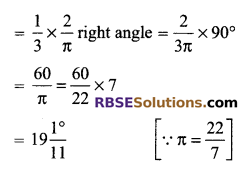
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 13 Angles and their Measurement Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 13 Angles and their Measurement Additional Questions, drop a comment below and we will get back to you at the earliest.