RBSE Solutions for Class 9 Maths Chapter 13 Angles and their Measurement Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 13 Angles and their Measurement Miscellaneous Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 13 |
| Chapter Name | Angles and their Measurement |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 15 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 13 Angles and their Measurement Miscellaneous Exercise
Multiple Choice Questions (Q1 to Q5)
Question 1.
The line describing (RBSESolutions.com) an angle of 750°, lies in:
(A) First quadrant
(B) Second quadrant
(C) Third quadrant
(D) Fourth quadrant
Solution.
(A) First quadrant
Question 2.
The number of radians in angle 30° is:
(A) \(\frac { \pi }{ 3 }\) radian
(B) \(\frac { \pi }{ 4 }\) radian
(C) \(\frac { \pi }{ 6 }\) radian
(D) \(\frac { 3\pi }{ 4 }\) radian
Solution.
(C) \(\frac { \pi }{ 6 }\) radian
![]()
Question 3.
The value of \(\frac { 3\pi }{ 4 }\) in sexagesimal system is:
(A) 75°
(B) 135°
(C) 120°
(D) 220°
Solution.
(B) 135°
Question 4.
The time is taken by the minute hand of (RBSESolutions.com) a watch in tracing an angle of \(\frac { \pi }{ 6 }\) radians is:
(A) 10 minutes
(B) 20 minutes
(C) 15 minutes
(D) 5 minutes
Solution.
(D) 5 minutes
Question 5.
The value of the angle, in radian subtended at the centre of the circle of radius 100 metres by an arc of length 25π metres is:
(A) \(\frac { \pi }{ 4 }\) radian
(B) \(\frac { \pi }{ 3 }\) radian
(C) \(\frac { \pi }{ 6 }\) radian
(D) \(\frac { 3\pi }{ 4 }\) radian
Solution.
(A) \(\frac { \pi }{ 4 }\) radian
Question 6.
In which quadrant does (RBSESolutions.com) the revolving ray lie when it makes the following angles.
(i) 240°
(ii) 425°
(iii) -580°
(iv) 1280°
(v) -980°
Solution.
(i) 240° = 2 x right angle +60°, therefore the position of the revolving ray will be in third quadrant.
(ii) 425° = 4 x right angles +65°, therefore the position of the revolving ray will be in first quadrant.
(iii) -580° = – 6 x right angles -40°, therefore the position of the revolving ray will be in second quadrant.
(iv) 1280° = 14 x right angles +20°, therefore the position of the revolving ray will be in third quadrant.
(v) – 980° = – 10 x right angles -80°, therefore the position of the revolving ray will be in second quadrant.
Question 7.
Convert the following angles in radians:
(i) 45°
(ii) 120°
(iii) 135°
(iv) 540°
Solution.

![]()
Question 8.
Express the following angles (RBSESolutions.com) in sexagesimal system.
(i) \(\frac { \pi }{ 2 }\)
(ii) \(\frac { 2\pi }{ 5 }\)
(iii) \(\frac { 5\pi }{ 6 }\)
(iv) \(\frac { \pi }{ 15 }\)
Solution.

Question 9.
Find the angle in radians subtended at the centre of (RBSESolutions.com) a circle of radius 5 cm by an arc of the circle whose length is 12 cm.
Solution.
We know that:
θ(radian) = \(\frac { arc length }{ radius }\)
We have, radius = 5 cm and arc length = 12 cm
θc = \(\frac { 12 }{ 5 }\)
Question 10.
How much time the minute hand of a watch will take (RBSESolutions.com) to describe an angle of \(\frac { 3\pi }{ 2 }\) radians.
Solution.
Time taken by the minute hand of a watch in tracing 4 right angles or an angle equal to 2π radians = 1 hour.
Time taken by the minute hand of a clock in tracing an angle equal to 1 radian = \(\frac { 1 }{ 2\pi }\) hours
Time taken by the minute hand of a clock in tracing an angle equal to \(\frac { 3\pi }{ 2 }\) radians
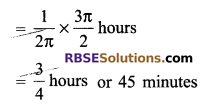
Question 11.
How much time the minute hand of (RBSESolutions.com) a watch will take to describe an angle of 120°?
Solution.
We know that:
The minute hand of a watch describes an angle of 4 right angles i.e. 360° in one hour.
the time taken by minute hand to trace 1° = \(\frac { 1 }{ 360 }\) hours
the time taken by minute hand to trace 120° angle = \(\frac { 1 }{ 360 }\) x 120 = \(\frac { 1 }{ 3 }\) hours
= \(\frac { 1 }{ 3 }\) x 60 minutes = 20 minutes.
Question 12.
Find the radius of the circle, if any (RBSESolutions.com) arc length of 10 cm subtends an angle of 60° at the centre of the circle.
Solution.

Question 13.
Find the time if the minute hand of (RBSESolutions.com) a clock has revolved through 30 right angles just after noon.
Solution.
We know that:
The time taken by the minute hand of a clock in tracing 4 right angles is 1 hour.
So, we convert 30 right angles in terms of the multiple of 4 right angles
i.e. 30 right angles
= 7 x (4 right angles) + 2 right angles
= 7 x 1 hr + \(\frac { 1 }{ 2 }\) hr = 7\(\frac { 1 }{ 2 }\) hours
= 7 hours 30 minutes
Hence, time = 7 : 30 p.m.
![]()
Question 14.
The angles of a triangle are (RBSESolutions.com) in the ratio of 2 : 3 : 4. Find all the three angles in radians.
Solution.
The A, B and C are angles of any triangle ABC
A : B : C = 2 : 3 : 4
⇒ ∠A = 2x, ∠B = 3x and ∠C = 4x
∠A + ∠B + ∠C = 180° (Angles sum property of a triangle)
⇒ 2x + 3x + 4x = 180°
⇒ 9x = 180°
x = 20°
Therefore angles (in degrees) are 40°, 60° and 80°
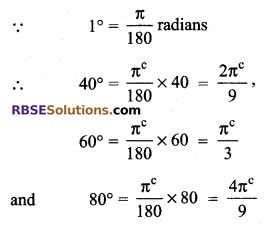
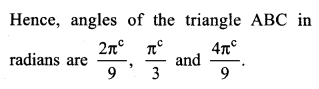
Question 15.
Convert \(\frac { 3\pi }{ 5 }\) radian (RBSESolutions.com) into sexagesimal system.
Solution.

We hope the given RBSE Solutions for Class 9 Maths Chapter 13 Angles and their Measurement Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 13 Angles and their Measurement Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.