RBSE Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Additional Questions

RBSE Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 9
Subject	Maths
Chapter	Chapter 14
Chapter Name	Trigonometric Ratios of Acute Angles
Exercise	Additional Questions
Number of Questions Solved	31
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Additional Questions

Multiple Choice Questions

Question 1.
The value of sec²50° – tan²50° is (RBSESolutions.com) equal to:
(A) -1
(B) 0
(C) 1
(D) 2

Question 2.

Question 3.

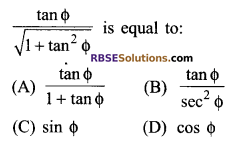
Question 4.

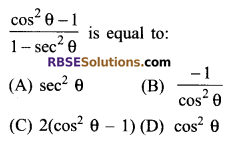
Question 5.
If 3 cot φ = 2 then the (RBSESolutions.com) value of cosec²φ is equal to:
(A) \(\frac { \surd 3 }{ 3 }\)
(B) \(\frac { 13 }{ 9 }\)
(C) \(\frac { 9 }{ 13 }\)
(D) \(\frac { 3 }{ \surd 3 }\)

Answers

1. C
2. A
3. C
4. D
5. B

Very Short Answer Type Questions

Question 1.
Write the value (RBSESolutions.com) of cosec²50° – cot²50°
Solution.
cosec²θ – cot²θ = 1
cosec²50° – cot²50° = 1

Question 2.
Prove that

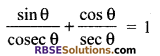
Solution.

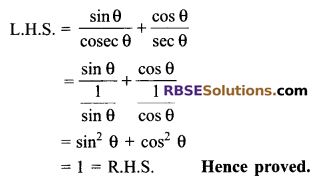
Question 3.
Prove that
sin θ cosec θ + cos θ sec θ = 2.
Solution.

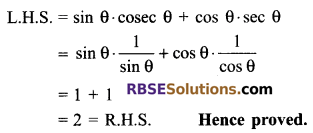
Question 4.
Prove that

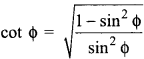
Solution.

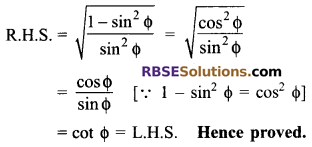
Question 5.
Write the (RBSESolutions.com) value of (1 – cos θ)(1 + cos θ)(1 + cot²θ).
Solution.

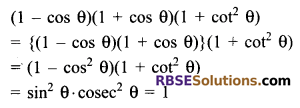
Question 6.
If cos²θ – sin²θ = \(\frac { 1 }{ 2 }\) , find the value of cos⁴θ – sin⁴θ
Solution.
Expression
cos⁴θ – sin⁴θ

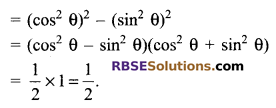
Question 7.
Prove that
tan²A + tan⁴A = sec⁴A – sin²A.
Solution.
L.H.S. = tan²A + tan⁴A
= tan²A (1 + tan²A)
= (sec²A – 1) sec²A
= sec⁴A – sec²A
= R.H.S.

Question 8.
Find the (RBSESolutions.com) value of

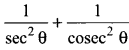
Solution.

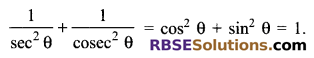
Question 9.
Find the value of (cos²θ – 1)(1 + cot²θ).
Solution.

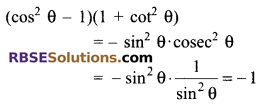
Question 10.
Evaluate (1 – sin²θ)(1 + tan²θ).
Solution.

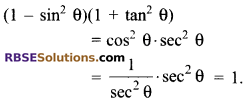
Short Answer Type Questions

Question 1.

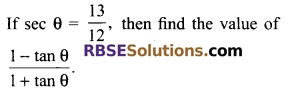
Solution.

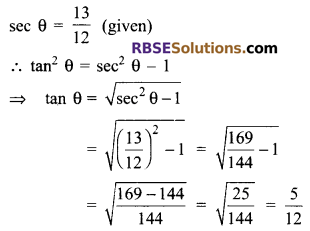
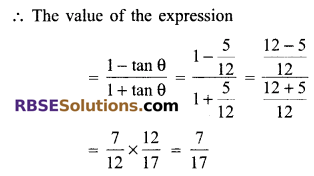
Question 2.
In any triangle ABC, if ∠B = 90° and side AB = 4 cm and AC = 5 cm, then (RBSESolutions.com) find side BC.
Solution.

Question 3.

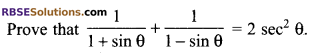
Solution.

Question 4.
Prove that sec A (1 – sin A)(sec A + tan A) = 1
Solution.

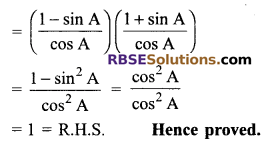
Question 5.
Prove that

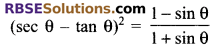
Solution.

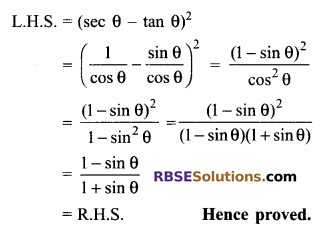
Question 6.
Prove that

Solution.

Question 7.
Prove that
tan²φ + cot²φ + 2 = sec²φ cosec²φ
Solution.

Question 8.
If sin x + sin²x = 1, show that cos²x + cos⁴x = 1.
Solution.
sin x + sin²x = 1
⇒ sin x = 1 – sin²x
⇒ sin x = cos²x
Squaring both (RBSESolutions.com) the sides, we get
sin²x = cos⁴x
⇒ 1 – cos²x = cos⁴x
⇒ 1 = cos²x + cos⁴x
Hence proved.

Question 9.
Prove that cos²θ (1 + tan²θ) + sin²θ (1 + cot²θ) = 2
Solution.

Question 10.
If sin θ + cos θ = a and sin θ – cos θ = b then prove that a² + b² = 2.
Solution.
sin θ + cos θ = a …(i)
and sin θ – cos θ = b …(ii)
Squaring eqns. (i) and (ii) and (RBSESolutions.com) then adding
(sin θ + cos θ)² + (sin θ – cos θ)² = a² + b²
⇒ sin²θ + cos²θ + 2 sin θ cos θ + sin²θ + cos²θ – 2 sin θ cos θ = a² + b²
⇒ 1 + 1 = a² + b²
⇒ a² + b² = 2
Hence proved.

Long Answer Type Questions

Question 1.
Prove that (sec A – cos A)(cosec A – sin A) = \(\frac { 1 }{ tanA+cotA }\)
Solution.

Question 2.
Prove that sin θ (1 + tan θ) + cos θ (1 + cot θ) = sec θ + cosec θ.
Solution.

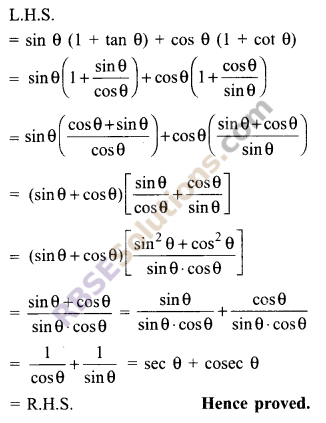
Question 3.

Solution.

Question 4.

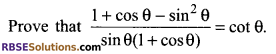
Solution.

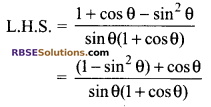
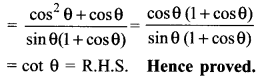
Question 5.
Prove that sec⁶θ = tan⁶θ + 3 tan²θ sec²θ + 1.
Solution.

Question 6.
Prove that

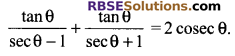
Solution.

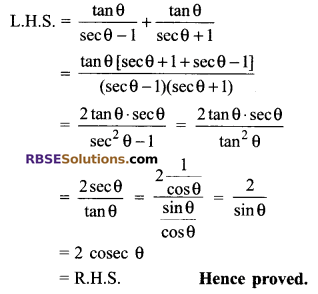
We hope the given RBSE Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Additional Questions, drop a comment below and we will get back to you at the earliest.