RBSE Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | Trigonometric Ratios of Acute Angles |
| Exercise | Exercise 14.2 |
| Number of Questions Solved | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2
Solve the following by using trigonometric identities (1 to 10)
Question 1.
If cosec A = \(\frac { 5 }{ 4 }\), then (RBSESolutions.com) evaluate cot A, sin A and cos A.
Solution.
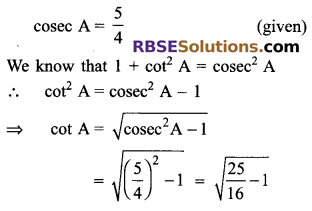

![]()
Question 2.
If tan A = \(\frac { 20 }{ 21 }\), then (RBSESolutions.com) evaluate cos A and sin A.
Solution.

Question 3.
If sin A = \(\frac { 3 }{ 5 }\), then (RBSESolutions.com) evaluate cos A and tan A.
Solution.

Question 4.
If cos B = \(\frac { 1 }{ 4 }\), then find (RBSESolutions.com) the remaining trigonometrical ratios.
Solution.


![]()
Question 5.
If sin A = \(\frac { 5 }{ 13 }\), then (RBSESolutions.com) evaluate cos A and tan A.
Solution.

Question 6.
If tan A = √2 – 1, then prove that sin A cos A = \(\frac { 1 }{ 2\surd 2 }\)
Solution.

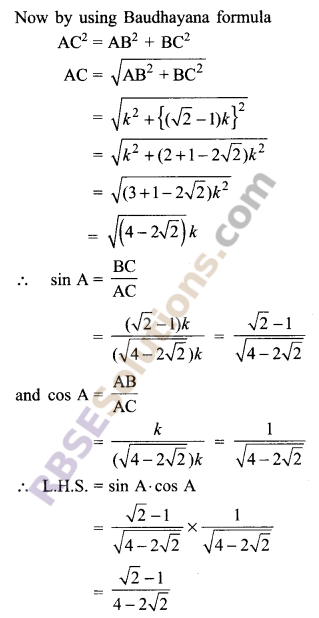

Question 7.
If tan A = 2, then (RBSESolutions.com) evaluate sec A . sin A + tan2A – cosec A.
Solution.
tan A = 2 (given)

![]()
Question 8.
If sin θ = \(\frac { 4 }{ 5 }\) then (RBSESolutions.com) evaluate \(\frac { 4tan\theta -5cos\theta }{ sec\theta +4cos\theta }\)
Solution.

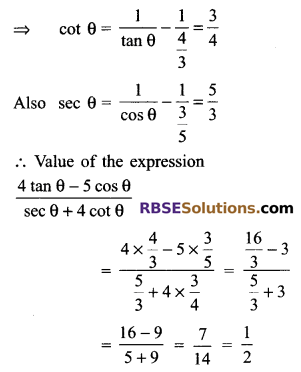
Question 9.
If cos θ = \(\frac { 1 }{ \surd 2 }\), then (RBSESolutions.com) evaluate sin θ and cot θ
Solution.
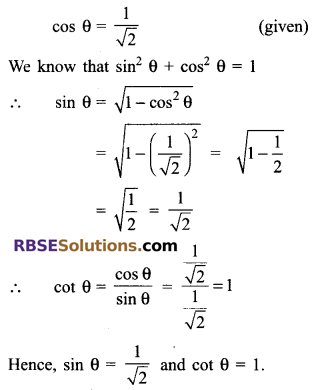
Question 10.
If sec θ = 2, then evaluate tan θ, cos θ and sin θ.
Solution.
sec θ = 2 (given)
We know that 1 + tan2θ = sec2θ
tan2θ = sec2θ – 1
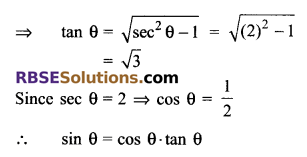
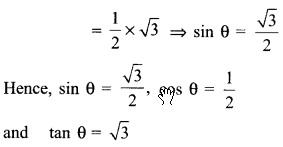
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 14 Trigonometric Ratios of Acute Angles Ex 14.2, drop a comment below and we will get back to you at the earliest.