RBSE Solutions for Class 9 Maths Chapter 2 Number System Ex 2.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 2 Number System Exercise 2.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Number System |
| Exercise | Ex 2.1 |
| Number of Questions Solved | 5 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 2 Number System Ex 2.1
Question 1.
Classify the following numbers (RBSESolutions.com) as rational or irrational:
(i) √23
(ii) √225
(iii) 0.3796
(iv) 7.478478…
(v) 1.101001000100001…
Solution.
(i) √23
Here, 23 is not a perfect square number, hence, √23 is an irrational number.
(ii) √225
Here 225 is (RBSESolutions.com) a perfect square of 15, hence √225 is a rational number.
(iii) 0.3796 can be written in \(\frac { p }{ q }\) form,
where q ≠ 0 i.e \(\frac { 3796 }{ 10000 }\)
Hence, it is a rational number.
(iv) 7.478478 i.e. \(7.\bar { 478 } \)
Here, pair of digits (478) are repeating as it is non-terminating but recurring.
(v) 1.101001000100001…. is an irrational number is its decimal expansion is non-terminating and non-recurring.
![]()
Question 2.
Write three numbers whose decimal (RBSESolutions.com) expansions are non-terminating non-recurring.
Solution.
The three numbers whose decimal expansions are non-terminating non-recurring i.e. irrational numbers are
0.01001000100001…..
0.02002000200002….
0.03003000300003…….. etc.
Question 3.
Write the following in decimal form and say what (RBSESolutions.com) kind of decimal expansion each has:
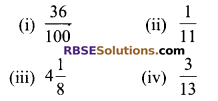

Solution.

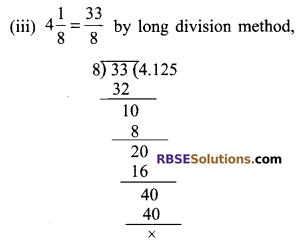



Question 4.
Express the following in the form \(\frac { p }{ q }\), where p and q are (RBSESolutions.com) integers and q ≠ 0.

Solution.
(i) Let x = \(0.\bar { 3 } \)
i.e., x = 0.3333 …(i)
Multiplying (i) by 10, we get
10x = 3.3333 …(ii)
Subtracting (i) from (ii),
we get 10x – x = 3.3333… – 0.3333…
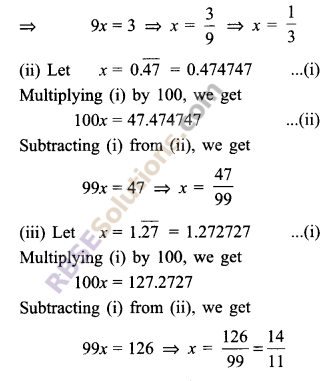

![]()
Question 5.
Find three different irrational numbers between (RBSESolutions.com) the rational numbers \(\frac { 5 }{ 7 }\) and \(\frac { 9 }{ 11 }\).
Solution.

There are infinite irrational numbers between the two given numbers, we may choose any three of them, e.g.
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 2 Number System Ex 2.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Solutions Chapter 2 Number System Exercise 2.1, drop a comment below and we will get back to you at the earliest.