RBSE Solutions for Class 9 Maths Chapter 3 बहुपद Ex 3.2 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 3 बहुपद Exercise 3.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | बहुपद |
| Exercise | Exercise 3.2 |
| Number of Questions Solved | 4 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 3 बहुपद Ex 3.2
प्रश्न 1.
बहुपद 2x3 – 13x2 + 17x + 12 के मान x के निम्नलिखित मानों पर ज्ञात कीजिए।
(i) x = 2
(ii) x = -3
(iii) x = 0
(iv) x = -1
हल
माना, p(x) = 2x3 – 13x2 + 17x + 12 ….(i)
(i) समीकरण (i) में = 2 रखने पर,
p(2) = 2(2)3 – 13(2)2 + 17(2) + 12
=2 x 8 – 13 x 4 + 34 + 12
= 16 – 52 + 34 + 12
= 10
(ii) समीकरण (i) में x = -3 रखने, पर,
p(-3) = 2 (-3)3 – 13(-3)2 + 17(-3) + 12
= 2 x (-27) – 13 x 9 – 17 x 3 + 12
= -54 – 117 – 51 + 12
= -210
(iii) समीकरण (i) में x = 0 रखने पर,
p(0) = 2(0)3 – 13(0)2 +17(0) + 12
= 0 – 0 + 0 + 12
= 12
(iv) समीकरण (i) में x = -1 रखने पर
p(-1) = 2(-1)3 – 13(-1)2 + 17(-1) + 12
= -2 – 13 – 17 + 12
= -20
![]()
प्रश्न 2.
निम्नलिखित बहुपदों में से(RBSESolutions.com)प्रत्येक बहुपद के लिए P(2), P(1) और P(0) का मान ज्ञात कीजिए।
(i) p(x) = x2 – x + 1
(ii) p(y) = (y + 1)(y – 1)
(iii) p(x) = x3
(iv) p(t) = 2 + t + t2 – t3
हल
(i) p(x) = x2 – x + 1
p(2) = 22 – 2 + 1 = 4 – 2 + 1 = 3
p(1) = 12 – 1 + 1 = 1 – 1 + 1 = 1
p(0) = 02 – 0 + 1 = 0 – 0 + 1 = 1
(ii) p(y) = (y + 1) (y – 1)
p(2) = (2 + 1) (2 – 1) = 3 x 1 = 3
p(1) = (1 + 1) (1 – 1) = 2 x 0 = 0
p(0) = (0 + 1) (0 – 1) = 1 x (-1) = -1
(iii) p(x) = x3
p(1) = 13 = 1
p(2) = 23 = 8
p(0) = 03 = 0
(iv) p(t) = 2 + t + t2 – t3
p(2) = 2 + 2 + 22 – 23 = 2 + 2 + 4 – 8 = 0
p(1) = 2 + 1 + 12 – 13 = 2 + 1 + 1 – 1 = 3
p(0) = 2 + 0 + 02 – 03 = 2 + 0 + 0 – 0 = 2
![]()
प्रश्न 3.
निम्नलिखित बहुपदों के सम्मुख अंकित मान बहुपद के शून्यक हैं, सत्यापित कीजिए।
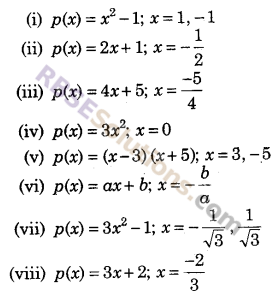
हल


![]()
प्रश्न 4.
निम्नलिखित बहुपदों के शून्यक ज्ञात कीजिए।
(i) p(x) = x – 4
(ii) p(x) = 4x
(iii) p(x) = bx, b ≠ 0
(iv) p(x) = x + 3
(v) p(x) = 2x – 1
(vi) p(x) = 3x + 7
(vii) p(x) = cx + d, c ≠ 0, c, d वास्तविक संख्याएँ हैं।
हल
बहुपद p(x) के शून्यक ज्ञात करने के लिए, p(x) = 0
(i) दिया व्यंजक, p(x) = x – 4
p(x) = 0 ⇒ x – 4 = 0 ⇒ x = 4
अतः p(x) का शून्यक 4 है।
(ii) दिया व्यंजक, p(x) = 4x
p(x) = 0 ⇒ 4x = 0 ⇒ x = 0
अतः p(x) को शून्यक 0 है।
(iii) दिया व्यंजक, p(x) = bx, b ≠ 0
p(x) = 0 ⇒ bx = 0 ⇒ x = 0
अत: p (x) का शून्यक 0 है।
(iv) दिया(RBSESolutions.com)व्यंजक, p(x) = x + 3
p (x) = 0 ⇒ x + 3 = 0 ⇒ x = -3
अत: p (x) का शून्यक -3 है।
(v) दिया व्यंजक, p (3) = 2x – 1
p (x) = 0 ⇒ 2x – 1 = 0 ⇒ 2x = 1 ⇒ x = \(\frac { 1 }{ 2 }\)
अत: p (3) का शून्यक \(\frac { 1 }{ 2 }\) है।
(vi) दिया व्यंजक, p (x) = 3x + 7
p (x) = 0 ⇒ 3x + 7 = 0 ⇒ 3x = -7 ⇒ x = \(\frac { -7 }{ 3 }\)
अत: p (x) का(RBSESolutions.com)शून्यक -7/3 है।
(vii) दिया व्यंजक, p (x) = cx + d, c ≠ 0, c, d वास्तविक संख्याएँ हैं।
p (x) = 0 ⇒ cx + d = 0 ⇒ cx = -d
⇒ x = \(\frac { -d }{ c }\)
अत: p(x) का शून्यक \(\frac { -d }{ c }\) है।
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 3 बहुपद Ex 3.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 3 बहुपद Exercise 3.2, drop a comment below and we will get back to you at the earliest.