RBSE Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.2 is part of RBSE Solutions for Class 9 Maths. Here we have given RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.2.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Polynomial |
| Exercise | Ex 3.2 |
| Number of Questions Solved | 4 |
| Category | RBSE Solutions |
RBSE Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.2
Question 1
Find the value of the (RBSESolutions.com) polynomial 2x3 – 13x2 + 17x + 12 at
(i) x = 2
(ii) x = – 3
(iii) x = 0
(iv) x = – 1
Solution.
Let p(x) = 2x3 – 13x2 + 17x + 12
(i) p(2) = 2(2)3 – 13(2)2 + 17(2) + 12
= 16 – 52 + 34 + 12
= 62 – 52 = 10
(ii) p(-3) = 2(-3)3 – 13(-3)2 + 17(-3) + 12
= – 54 – 117 – 51 + 12
= – 222 + 12
= – 210
(iii) p(0) = 2(0)3 – 13(0)2 + 17(0) + 12
= 0 – 0 + 0 + 12
= 12
(iv) p(-1) = 2(- 1)3 – 13(-1)2 + 17(- 1) + 12
= – 2 – 13 – 17 + 12
= – 32 + 12
= – 20
![]()
Question 2.
Find p(2), p(1) and p(0) for each (RBSESolutions.com) of the following polynomials.
(i) p(x) = x2 – x + 1
(ii) p(y) = (y + 1)(y – 1)
(iii) p(x) = x3
(iv) p(t) = 2 + t + t2 – t3
Solution.
(i) The given polynomial is
p(x) = x2 – x + 1
∴ p(2) = 22 – 2 + 1 = 3
[replacing x by 2]
p(1) = 12 -1 + 1 = 1
[replacing x by 1]
p(0) = (0)2 – (0) + 1 = 1
[replacing x by 0]
(ii) The given (RBSESolutions.com) polynomial is
p(y) = (y + 1)(y – 1)
p(2) = (2 + 1)(2 – 1) = 3
p(1) = (1 + 1)(1 – 1) = 0
p(0) = (0 + 1)(0 – 1) = – 1 .
(iii) The given polynomial is p(x) = x3
p( 2) = 23 = 8
p(1) = 13 = 1
p(0) = 03 = 0
(iv) The given (RBSESolutions.com) polynomial is
p(t) = 2 + t + t2 – t3
p(2) = 2 + 2 + (2)2 – (2)3
= 8 – 8 = 0
p(1) = 2 + 1 + (1)2 – (1)3
= 4 – 1 = 3
p(0) = 2 + 0 + (0)2 – (0)3
= 2 – 0
= 2
Question 3.
Verify whether the following are (RBSESolutions.com) zeroes of the polynomial, indicated against them.
(i) p(x) = x2 – 1; x = 1,-1
(ii) p(x) = 2x + 1; x = \(x=\frac { -1 }{ 2 }\)
(iii) p(x) = 4x + 5; \(x=\frac { -5 }{ 4 }\)
(iv) p(x) = 3x2; x = 0
(v) p(x) = (x – 3)(x + 5); x = 3, – 5
(vi) p(x) = ax + b; \(x=\frac { -b }{ a }\)
(vii) p(x) = 3x2 – 1; \(x=\frac { -1 }{ \sqrt { 3 } } ,\frac { 1 }{ \sqrt { 3 } } \)
(viii) p(x) = 3x + 2; \(x=\frac { -2 }{ 3 }\)
Solution.
p(x) = x2 – 1; x = 1, – 1
∴ p(1) = (1)2 – 1
= 1 – 1 = 0
p(- 1) = (- 1)2 – 1
= 1 – 1 = 0
Yes, both 1,-1 are zeroes (RBSESolutions.com) of the polynomials p(x) = x2 – 1.
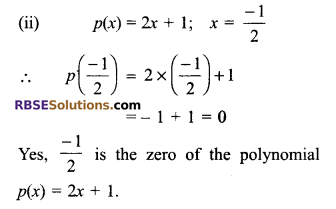

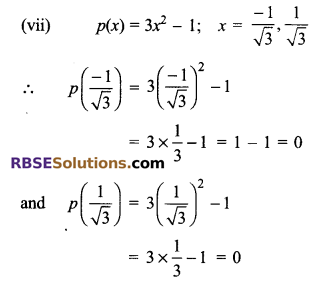
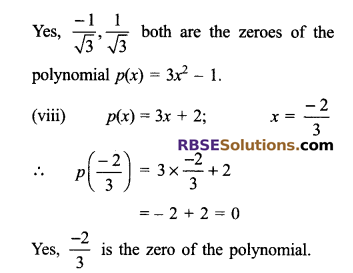
![]()
Question 4.
Find the zeroes of the (RBSESolutions.com) polynomial in each case.
(i) p(x) = x – 4
(ii) p(x) = 4x
(iii) p(x) = bx, b ≠ 0
(iv) p(x) = x + 3
(v) p(x) = 2x – 1
(vi) p(x) = 3x + 7
(vii) p(x) = cx + d, c ≠ 0, c and d are real numbers.
Solution.
For zeroes of the (RBSESolutions.com) polynomial, p(x) = 0
(i) x – 4 = 0 ⇒ x = 4
Hence, 4 is the zero of the polynomial p(x).
(ii) 4x = 0 ⇒ x = 0
Hence, 0 is the zero of the polynomial p(x).
(iii) bx = 0 ⇒ x = 0
Hence, 0 is the zero of the polynomial p(x).
(iv) x + 3 = 0 ⇒ x = – 3
Hence, – 3 is the zero (RBSESolutions.com) of the polynomial p(x).
(v) 2x – 1 = 0 ⇒ 2x = 1 ⇒ x = \(\frac { 1 }{ 2 }\)
Hence, \(\frac { 1 }{ 2 }\) is the zero of the polynomial p(x).
(vi) 3x + 7 = 0 ⇒ 3x = -7 ⇒ x = \(\frac { -7 }{ 3 }\)
Hence, \(\frac { -7 }{ 3 }\) is the zero of the polynomial p(x).
(vii) p(x) = cx + d, c ≠ 0, c and d are real numbers.
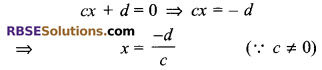
We hope the given RBSE Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.2 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.2, drop a comment below and we will get back to you at the earliest.