7417RBSE Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | दो चरों वाले रैखिक समीकरण |
| Exercise | Exercise 4.1 |
| Number of Questions Solved | 11 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1
निम्न समीकरणों को आलेखीय विधि से हल कीजिए-
प्रश्न 1.
x + 3y = 6
2x – 3y = 6
हल
1. दिया गया समीकरण निकाय है:
x + 3y = 6 …(1)
2x – 3y = 12 …(2)
चूँकि दोनों समीकरण x व y की प्रथम घात में हैं। इसलिए इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण x + 3y = 6 या y = \(\frac { 6-x }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है।

इस प्रकार, समीकरण 2x – 3y = 12 या y = \(\frac { 2x-12 }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दु (3, 1), (0, 2) तथा (-3, 3) का(RBSESolutions.com)आलेखन करं मिलाने से समीकरण x + 3y = 6 का आलेख तथा (0, -4), (3, -2) तथा 6,0) का आलेखन कर मिलाने से समीकरण 2x – 3y = 12 का आलेख प्राप्त होता है।
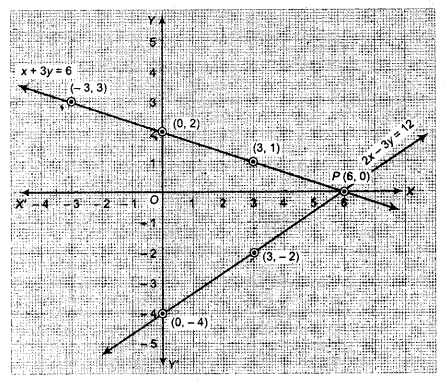
ये आलेख (सरल रेखाएँ) बिन्दु P पर प्रतिच्छेदित होते हैं, जिसके निर्देशांक (6,0) हैं। अत: x = 6, y = 0 दिए गए समीकरण निकाय का अद्वितीय हल है।
![]()
प्रश्न 2.
2x + y = 12
2x – y + 2 = 0
हल
दिया गया समीकरण निकाय है:
2x + y = 6 ……. (i)
2x – y + 2 = 0 ……(ii)
चूंकि दोनों समीकरण x वे y की प्रथम घात में हैं। इसलिए इनके(RBSESolutions.com)आलेख सरल रेखाएँ होंगी।
अब समीकरण 2x + y = 6 या y = 6 – 2x से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इस प्रकार, समीकरण 2x – y + 2 = 0 या y = 2x + 2 से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (1, 4), (2, 2) तथा (3, 0) का आलेखन कर मिलाने से समीकरण 2x + y = 6 का आलेख तथा (0, 2), (1, 4) तथा (2, 6) का आलेखन कर मिलाने से समीकरण 2x – y + 2 = 0 का आलेख प्राप्त होता है।
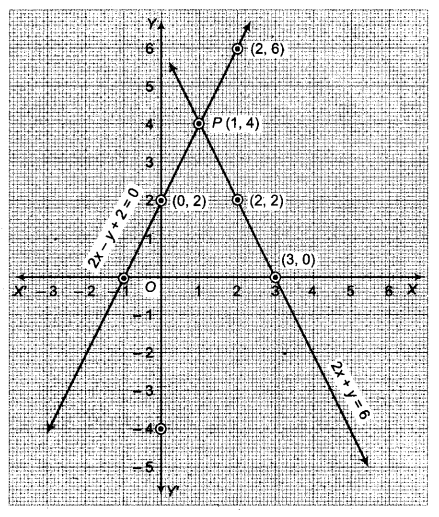
ये आलेख (सरल रेखाएँ) बिन्दु P पर प्रतिच्छेदित होते हैं, जिसके निर्देशांक (1,4) हैं। अतः x = 1, y = 4 दिए गए समीकरण का अद्वितीय हल हैं।
![]()
प्रश्न 3.
x – 2y = 6
3x – 6y = 0
हल
दिया गया समीकरण निकाय है
x – 2y = 6 …(i)
3x – 6y = 0 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं।
इसलिए इनके आलेख(RBSESolutions.com)सरल रेखाएँ होंगी।
अब समीकरण x – 2y = 6 या y = \(\frac { x-6 }{ 2 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 3x – 6y = 0 या y = \(\frac { x }{ 2 }\) से (x, y) के विभिन्न मानों से निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (0, -3), (6, 0) तथा (2, -2) का आलेखन कर मिलाने से समीकरण x – 2y = 6 का आलेख तथा (2, 1), (4, 2) तथा (6, 3) का आलेखन कर मिलाने से समीकरण 3x – 6y = 0 का आलेख प्राप्त होता है।
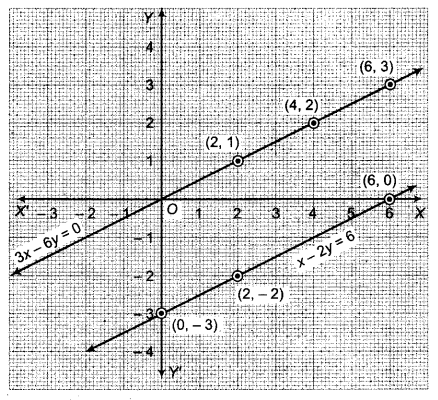
ये सरल रेखाएँ (आलेख) एक दूसरे को प्रतिच्छेदित नहीं करती हैं। अतः दिए गए समीकरण निकाय का कोई हल नहीं हैं।
![]()
प्रश्न 4.
x + y = 4
2x – 3y = 3
हल
दिया गया समीकरण निकाय-
x + y = 4 …(i)
2x – 3y = 3 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं। इसलिए इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण x + y = 4 या y = 4 – x से (x, y) के विभिन्न मानों(RBSESolutions.com)की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 2x – 3y = 3 या y = \(\frac { 2x-3 }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-
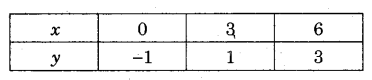
अब बिन्दुओं (1, 3), (2, 2) तथा (3, 1) का आलेखन कर मिलाने से समीकरण x + y = 4 का आलेख तथा (0, -1), (3, 1) तथा (6, 3) का आलेखन कर मिलाने से समीकरण 2x – 3y = 3 का आलेख प्राप्त होता है।
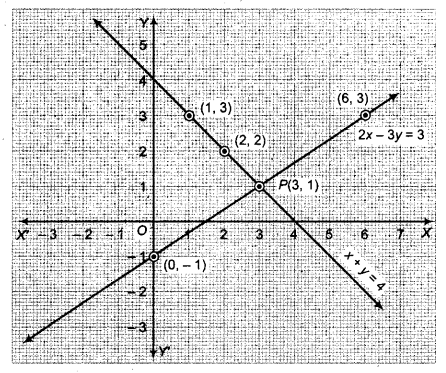
ये सरल रेखाएँ (आलेख) बिन्दु P पर प्रतिच्छेदित होती हैं जिसके निर्देशांक (3, 1) हैं। अतः x = 3 तथा y = 1 दिए गए समीकरण निकाय के अद्वितीय हल हैं।
![]()
प्रश्न 5.
2x – 3y + 13 = 0
3x – 2y + 12 = 0
हल
दिया गया समीकरण निकाय है:
2x – 3y + 13 = 0 …(i)
3x – 2y + 12 = 0 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात(RBSESolutions.com)में हैं। इसलिए इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण 2x – 3y + 13 = 0 या y = \(\frac { 2x+13 }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है।

इसी प्रकार, समीकरण 3x – 2y + 12 = 0 या y = \(\frac { 3x+12 }{ 2 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है।

अब बिन्दुओं (-2, 3), (-3.5, 2) तथा (-0.5, 4) का आलेखन कर मिलाने से समीकरण 2x – 3y + 13 = 0 का आलेख तथा (-2, 3), (0, 6) तथा (-4, 0) का आलेखन कर मिलाने से समीकरण 3x – 2y + 12 = 0 का आलेख प्राप्त होता है।
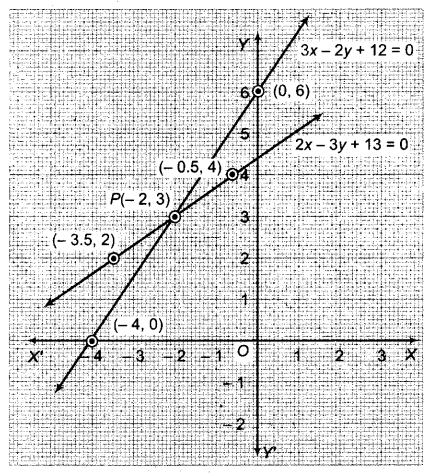
ये आलेख (सरल रेखाएँ) बिन्दु P पर प्रतिच्छेदित होते हैं, जिसके निर्देशांक (-2, 3) हैं। अतः x = -2, y = 3 दिए गए समीकरण निकाय का अद्वितीय हल है।
![]()
प्रश्न 6.
3x – 4y = 1
-2x + \(\frac { 8 }{ 3 }\) y = 5
हल
दिया गया समीकरण निकाय है:
3x – 4y = 1 …(i)
-2x + \(\frac { 8 }{ 3 }\) y = 5 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं।
अत: इनके आलेख(RBSESolutions.com)सरल रेखाएँ होंगी।
अब समीकरण 3x – 4y = 1 या y = \(\frac { 3x-1 }{ 4 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण -2x + \(\frac { 8 }{ 3 }\) y = 5 या y = \(\frac { 3(5+2x) }{ 8 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (-1, -1), (3, 2) तथा (-5, -4) का आलेखन कर मिलाने से समीकरण 3x – 4y = 1 का आलेख तथा (1.5, 3), (3.5, 4.5) तथा (-4.5, -1.5) का आलेखन कर मिलाने से समीकरण -2x + \(\frac { 8 }{ 3 }\) y = 5 का आलेख प्राप्त होता है।
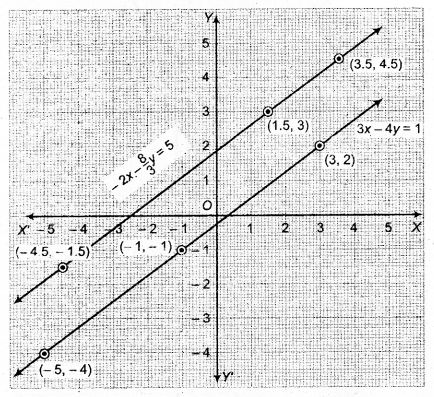
ये सरल रेखाएँ परस्पर प्रतिच्छेदित नहीं करती हैं। अतः इस समीकरण युग्म का कोई हल नहीं है।
![]()
प्रश्न 7.
2x + \(\frac { y }{ 2 }\) – 5 = 0
\(\frac { x }{ 2 }\) + y = -4
हल
दिया गया समीकरण निकाय है :
2x + \(\frac { y }{ 2 }\) – 5 = 0 …… (i)
\(\frac { x }{ 2 }\) + y = -4 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घांत में हैं। इसलिए इनके आलेख(RBSESolutions.com)सरल रेखाएँ होंगी। समीकरण 2x + \(\frac { y }{ 2 }\) – 5 = 0 या y = 2 (5 – 2x) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण \(\frac { x }{ 2 }\) + y = -4 या y = -4 – \(\frac { x }{ 2 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती हैं-

अब बिन्दुओं (3, -2), (1, 6) तथा (2, 2) का आलेखन कर मिलाने से समीकरण 2x + \(\frac { y }{ 2 }\) – 5 = 0 का आलेख तथा (2, -5), (-2, -3) तथा (0, -4) का आलेखन कर मिलाने से समीकरण \(\frac { x }{ 2 }\) + y = -4 का आलेख प्राप्त होता है।
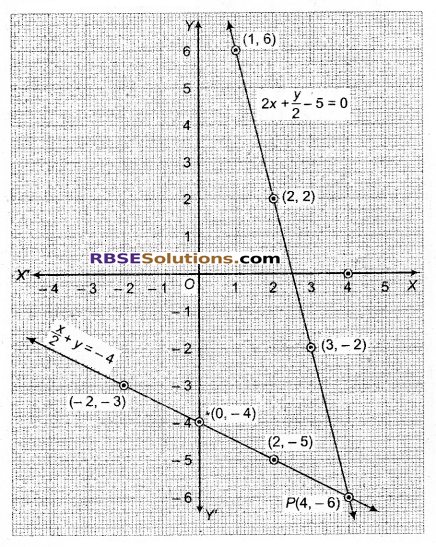
ये दोनों सरल रेखाएँ (आलेख) बिन्दु P पर प्रतिच्छेदित होती हैं जिसके निर्देशांक (4, -6) हैं।
अतः x = 4, y = -6 दिए गए(RBSESolutions.com)समीकरण निकाय का अद्वितीय हल हैं।
![]()
प्रश्न 8.
0.3x + 0.4y = 32; 0.6x + 0.8y = 2.4
हल
दिया गया समीकरण निकाय है:
0.3x + 0.4y = 32 …(i)
0.6 + 0.8y = 24 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं। इसलिए इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण 0.3x + 0.4y = 3.2 या y = \(\frac { 32-3x }{ 4 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 0.6x + 0.8y = 2.4 या y = \(\frac { 24-6x }{ 8 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है।

अब बिन्दुओं (4, 5), (0, 8) तथा (2, 6.5) को आलेखन कर मिलाने से समीकरण 0.3x + 0.4y = 3.2 का आलेख तथा (0, 3), (2, 1.5) तथा (4, 0) का आलेखन कर मिलाने से समीकरण 0.6x + 0.8y = 2.4 का(RBSESolutions.com)आलेख प्राप्त होता है।
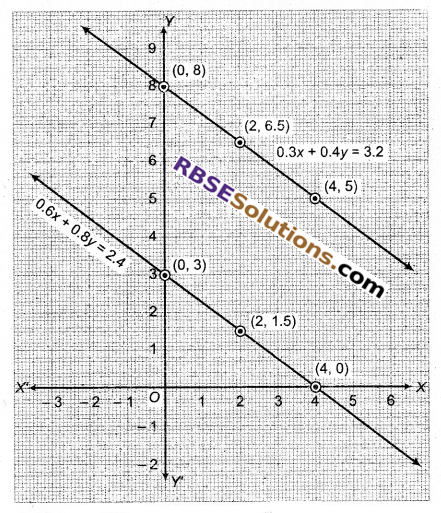
ये सरल रेखाएँ (आलेख) एक दूसरे को प्रतिच्छेद नहीं करती हैं। अतः इनका कोई हल नहीं है।
![]()
प्रश्न 9.
2x + 3y = 8; 4x – \(\frac { 3 }{ 2 }\) = 1
हल
दिया गया समीकरण निकाय है:
2x + 3y = 8 …(i)
4x – \(\frac { 3 }{ 2 }\) y = 1 …(ii)
चूँकि दोनों समीकरण ४ व y की प्रथम(RBSESolutions.com)घात में हैं। इसलिए इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण 2x + 3y = 8 या y = \(\frac { 8-2x }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 4x – \(\frac { 3 }{ 2 }\) y = 1 या y = \(\frac { 2(4x-1) }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (4, 0), (1, 2) तथा (-2, 4) का आलेखन कर मिलाने से समीकरण 2x + 3y = 8 का आलेख तथा (1, 2), (-2, 6) तथा (2.5, 6) का आलेखन कर मिलाने से समीकरण 4x – \(\frac { 3 }{ 2 }\) y = 1 का आलेख प्राप्त होता है।
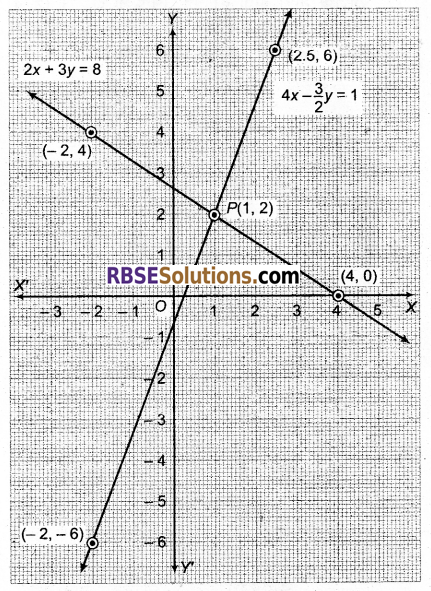
ये सरल रेखाएँ (आलेख) परस्पर बिन्दु P पर(RBSESolutions.com)प्रतिच्छेदित होती हैं, जिसके निर्देशांक (1, 2) हैं। अतः x = 1, y = 2 दिए गए समीकरण निकाय के अद्वितीय हल हैं।
![]()
प्रश्न 10.
3x – y = 2; 6x – 2y = 4
हल
दिया गया समीकरण निकाय है:
3x – y = 2 …(i)
6x – 2y = 4 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं। अतः इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण 3x – y = 2 या y = 3x – 2 से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 6x – 2y = 4 या y = \(\frac { 6x-4 }{ 2 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

qwwghni;अब बिन्दुओं (1, 1), (2, 4) तथा (-1, -5) का आलेखन कर मिलाने से समीकरण 3x – y = 2 का आलेख प्राप्त होता है।
पुनः बिन्दुओं (1, 1), (2, 4) तथा (3, 7) का आलेखन(RBSESolutions.com)कर मिलाने से समीकरण 6x – 2y = 4 का आलेख प्राप्त होता है।
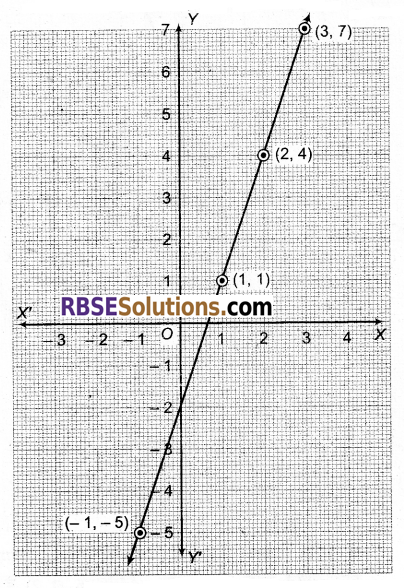
हम देखते हैं कि ये तीनों बिन्दु पहली रेखा 3x – y = 2 के आलेख पर विद्यमान हैं। अत: दोनों रेखाएँ सम्पाती होंगी। अतः दिया गया समीकरण निकाय संगत है तथा इसके अनन्त हल होंगे। अतः समीकरण 3x – y = 2 का प्रत्येक हल(RBSESolutions.com)इस निकाय का हल होगा।
![]()
प्रश्न 11.
3x + 2y = 0; 2x + y = -1
हल
दिया गया समीकरण निकाय
3x + 2y = 0 …(i)
2x + y = -1 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं।
अतः इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण 3x + 2y = 0 या y = \(\frac { -3 }{ 2 }\) x से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 2x + y = -1 या y = -1 – 2x से (3, 3) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (2, -3), (-2, 3) तथा (4, -6) का आलेखन कर मिलाने(RBSESolutions.com)से समीकरण 3x + 2y = 0 का आलेख तथा (1, -3), (-1, 1) तथा (2, -5) का आलेखन कर मिलाने से समीकरण 2x + y = -1 का आलेख प्राप्त होता है।
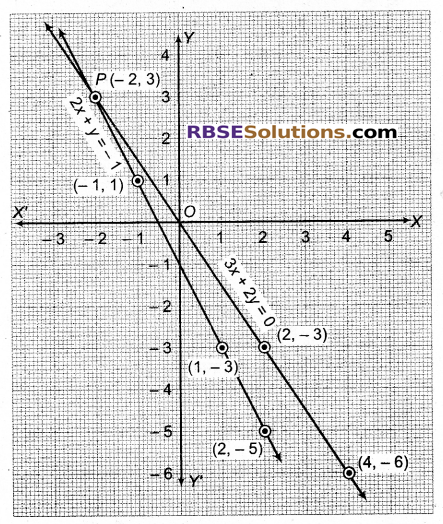
ये सरल रेखाएँ (आलेख) बिन्दु P पर(RBSESolutions.com)प्रतिच्छेदित होती हैं, जिसके निर्देशांक (-2, 3) हैं। अतः x = -2, y = 3 दिए गए निकाय का अद्वितीय हल हैं।
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.1, drop a comment below and we will get back to you at the earliest.