RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.3 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.3.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | Linear Equations in Two Variables |
| Exercise | Ex 4.3 |
| Number of Questions Solved | 7 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.3
In each of the following system of linear equation (RBSESolutions.com) determine whether the system of equations has a unique solution or no solution or infinitely many solutions. In case there is a unique solution, find it.
Question 1.
2x + y = 35
3x + 4y = 65
Solution
The given system of equations are
2x + y = 35
3x + 4y = 65
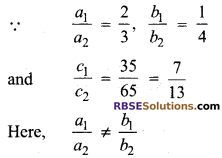
Hence, the given system of equations is (RBSESolutions.com) consistent and have unique solution.
2x + y = 35 …(i)
3x + 4y = 65 …(ii)
Multiplying equation (i) by 4 and subtracting (ii) from it, we get
5x = 75
⇒ x = 15
Putting x = 15 in equation (i), we get y = 5
Hence, x = 15 and y = 5 is the required unique solution.
![]()
Question 2.
2x – y = 6
x – y = 2
Solution
The given system (RBSESolutions.com) of equations are
2x – y = 6
x – y = 2
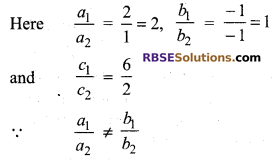
Hence the given system of equations (RBSESolutions.com) is consistent and have unique solution.
2x – y = 6 …(i)
x – y = 2 …(ii)
Subtracting (ii) from (i), we get x = 4
Putting the value of x in (ii), we get y = 2
Hence x = 4 and y = 2 is the required unique solution.
Question 3.
3x + 2y + 25 = 0
2x + y + 10 = 0
Solution
The given system of equations are
3x + 2y + 25 = 0
2x + y + 10 = 0
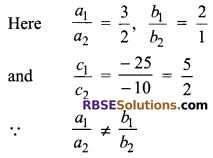
Hence the given system of equations (RBSESolutions.com) is consistent and hence it will have unique solution
3x + 2y + 25 = 0 …(i)
2x + y + 10 = 0 …(ii)
Multiplying equation (ii) by 2 and subtracting from equation (i), we get
-x + 5 = 0
x = 5
Putting the value of x in equation (i), we get
y = – 20
Hence, x = 5 and y = – 20 is the required unique solution.
Question 4.
x + 2y + 1 = 0
2x – 3y – 12 = 0
Solution
The given system (RBSESolutions.com) of equations are
x + 2y + 1 = 0
2x – 3y – 12 = 0
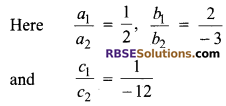
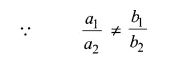
Hence, the given system of equations is consistent and it has unique solution.
x + 2y + 1 = 0 …(i)
2x – 3y – 12 = 0 …(ii)
Multiplying equation (i) by 2 and subtracting (ii) from it, we get
7y + 14 = 0
⇒ y = – 2
Putting the value of y in (RBSESolutions.com) equation (i), we get x = 3.
Hence, x = 3 and y = – 2 is the required unique solution.
Question 5.
Find the value of ‘k’ for which the system
(i) 2x + ky = 1, 3x – 5y = 7
(ii) kx + 2y = 5, 3x + y = 1 has no solution.
Solution.
(i) The system of equations are
2x + ky – 1 = 0 and 3x – 5y – 1 = 0
∴ For no (RBSESolutions.com) solution, condition is
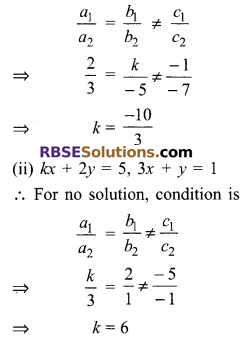
Question 6.
Solve the following (RBSESolutions.com) system of equations
mx – ny = m² + n²
x + y = 2m
Solution.
The given equations are
mx – ny = m² + n² …(i)
and x + y = 2m …(ii)
Multiplying equation (ii) by n and then adding, we get
(m + n)x = m² + n² + 2 mn
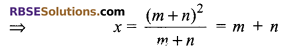
Substituting the (RBSESolutions.com) value of x in (ii), we get
(m + n) + y = 2m
⇒ y = 2m – m – n
⇒ y = m – n
Hence, required solution is m + n, m – n.
![]()
Question 7.
Find the value of ‘λ’ for which the system
3x + λy + 1 = 0
2x + y – 9 = 0 will have
(i) unique solution
(ii) no solution
Solution.
The given system (RBSESolutions.com) of equations are
3x + λy + 1 = 0 …(i)
2x + y – 9 = 0 …(ii)
Here we have

We hope the given RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.3 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.3, drop a comment below and we will get back to you at the earliest.