RBSE Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.4.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | दो चरों वाले रैखिक समीकरण |
| Exercise | Exercise 4.4 |
| Number of Questions Solved | 11 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4
निम्नलिखित समस्याओं का हल ज्ञात कीजिए।
प्रश्न 1.
दो अंकों की एक संख्या में इकाई का अंक दहाई के अंक का 3 गुना है। संख्या के 2 गुने में 10 जोड़ने पर प्राप्त नई संख्या में अंक परस्पर अपना स्थान बदल लेते हैं। संख्या ज्ञात कीजिए।
हल
माना इकाई का अंक = y तथा दहाई का अंक = x
संख्या = 10x + y तथा y = 3x …(i)
प्रश्नानुसार, 2(10x + y) + 10 = x + 10y
⇒ 20x + 2y + 10 = x + 10y
⇒ 20x – x + 2y – 10y = -10
⇒ 19x – 8y = -10
⇒ 19x – 8 × 3x = -10 (समी (i) से)
⇒ 19x – 24x = -10
⇒ -5x = -10
⇒ x = 2
समीकरण (i) में x = 2 रखने पर y = 3 x 2 = 6
अतः x = 2, y = 6
संख्या = 10x + y = 10 × 2 + 6 = 20 + 6 = 26
![]()
प्रश्न 2.
एक आयत का परिमाप 56 सेमी है। उसकी लम्बाई तथा चौड़ाई का अनुपात 4 : 3 है। आयत की लम्बाई एवं चौड़ाई ज्ञात कीजिए।
हल
आयत का परिमाप = 56 सेमी
माना आयत की(RBSESolutions.com)लम्बाई x तथा चौड़ाई y है।
तो 2 (x + y) = 56 या x + y = 28 …(i)

![]()
प्रश्न 3.
दो संख्याओं का अनुपात 3:4 है। यदि प्रत्येक संख्या में से 5 घटा दिया जाए, तो उनका अनुपात 5 : 7 हो जाता है। संख्याएँ ज्ञात कीजिए।
हल
माना दो संख्याएँ x व y हैं, तो x : y = 3 : 4

![]()
प्रश्न 4.
पिता की आयु अपने पुत्र की आयु के 6 गुना से 5 वर्ष अधिक है। 7 वर्ष पश्चात पिता की आयु पुत्र की आयु के 3 गुना से 3 अधिक होगी। दोनों की वर्तमान आयु ज्ञात कीजिए।
हल
माना पुत्र की वर्तमान आयु x वर्ष तथा पिता की वर्तमान आयु y वर्ष है। प्रथम शर्तानुसार,
y = 6x + 5
⇒ 6x – y = -5 …(i)
द्वितीय(RBSESolutions.com)शर्तानुसार,
y + 7 = 3 (x + 7) + 3
⇒ y + 7 = 3x + 21 + 3
⇒ y + 7 = 3x + 24
⇒ -3x + y = 24 – 7
⇒ -3x + y = 17 …(ii)
समीकरण (i) व (ii) को जोड़ने पर
6x – y – 3x + y = -5 + 17
3x = 12 ⇒ x = 4
x को मान समीकरण (i) में रखने पर
6 × 4 – y = -5
⇒ 24 – y = -5
⇒ y = 24 + 5 = 29
अतः पुत्र की आयु 4 वर्ष तथा पिता की आयु 29 वर्ष है।
![]()
प्रश्न 5.
राम ने श्याम से कहा कि “तुम मुझे अपने पास से 100 रुपए दे दो तो मेरे पास तुमसे 2 गुना(RBSESolutions.com)रुपए हो जाएँगे। तब श्याम ने राम से कहा कि “तुम यदि अपने पास से मुझे 10 रुपए दे दो तो मेरे पास तुमसे 6 गुना रुपए हो जाएँगे।” ज्ञात कीजिए कि दोनों के पास कितने-कितने रुपए हैं?
हल
माना राम के पास x रुपये तथा श्याम के पास y रुपये हैं।
प्रथम शर्तानुसार, x + 100 = 2 (y – 100)
⇒ x + 100 = 2y – 200
⇒ x – 2y = -300 …(i)
द्वितीय शर्तानुसार,
6 (x – 10) = (y + 10)
⇒ 6x – 60 = y + 10
⇒ 6x – y = 70 …(ii)
समीकरण (ii) को 2 से गुणा करके समीकरण (i) में से घटाने पर
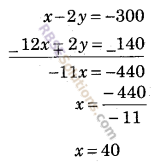
x का मान समीकरण (i) में रखने पर
40 – 2y = -300
⇒ -2y = -340
⇒ y = 170
अतः राम के पास 40 रुपये तथा श्याम के पास 170 रुपये हैं।
![]()
प्रश्न 6.
4 कुर्सियों और 3 मेजों का मूल्य 2100 रुपए है तथा 5 कुर्सियों और 2 मेजों का मूल्य 1750 रुपए है, तो एक कुर्सी तथा एक मेज का मूल्य ज्ञात कीजिए।
हल
माना एक कुर्सी का मूल्य x रुपए तथा एक मेज को मूल्य y रुपए हैं।
प्रथम शर्तानुसार, 4x + 3y = 2100 …..(i)
द्वितीय शर्तानुसार, 5x + 2y = 1750 ……(ii)
समीकरण (i) में 2 से तथा (ii) में -3 से गुणा करके जोड़ने पर
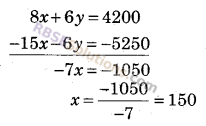
x का मान समीकरण (i) में रखने पर
4 × 150 + 3y = 2100
⇒ 600 + 3y = 2100
⇒ 3y = 2100 – 600 = 1500
⇒ y = 500
अत: एक कुर्सी का मूल्य 150 रुपए तथा मेज का मूल्य 500 रुपए है।
![]()
प्रश्न 7.
दो संख्याएँ इस प्रकार की हैं, कि बड़ी संख्या के 3 गुने में छोटी संख्या का भाग दिया जाता है, तो भागफल 4 तथा शेषफल 3 प्राप्त होता है और जब छोटी संख्या के 7 गुने में बड़ी संख्या का भाग(RBSESolutions.com)दिया जाता है, तो भागफल 5 तथा शेषफल 1 प्राप्त होता है। संख्याएँ ज्ञात कीजिए।
हल
माना बड़ी संख्या ४ तथा छोटी संख्या y है तो प्रथम शर्तानुसार, बड़ी संख्या के 3 गुने में छोटी संख्या का भाग दिया है, तो भागफल 4 तथा शेषफल 3 प्राप्त होता है-
(सूत्र- भाज्य = भाजक x भागफल + शेषफल से)
3x = y × 4 + 3
⇒ 3x = 4y + 3
⇒ 3x – 4y = 3 …(i)
इसी प्रकार, द्वितीय शर्तानुसार,
7y = x × 5 + 1
⇒ 7y = 5x + 1
⇒ 5x – 7y = -1 …(ii)
समीकरण (i) में 7 से तथा (ii) में -4 से गुणा करके परस्पर जोड़ने पर

अत: बड़ी संख्या 25 तथा छोटी संख्या 18 है।
![]()
प्रश्न 8.
दो अंकों की संख्या अपने अंकों के योग की 4 गुनी तथा अंकों के गुणनफल की 2 गुनी है। संख्या ज्ञात कीजिए।
हल
माना(RBSESolutions.com)इकाई का अंक x तथा दहाई का अंक y है तो संख्या x + 10y होगी।
प्रथम शर्तानुसार, x + 10y = 4 (x + y).
⇒ x + 10y = 4x + 4y
⇒ x – 4x + 10y – 4y = 0
⇒ 3x – 6y = 0
⇒ x – 2y = 0
⇒x = 2y …(i)
द्वितीय शर्तानुसार, x + 10y = 2 (x × y)
⇒ x + 10y = 2xy …(ii)
समीकरण (i) से x का मान समीकरण (ii) में रखने पर,
2y + 10y = 2 × 2y × y
⇒ 12y = 4y2
⇒ 4y2 = 12y
⇒ 4y = 12
⇒ y = 3
समीकरण (i) से, x = 2 × 3 = 6
संख्या = x + 10y = 6 + 10 × 3 = 6 + 30 = 36
![]()
प्रश्न 9.
एक भिन्न के अंश(RBSESolutions.com)तथा हर में 1 जोड़ने पर वह \(\frac { 4 }{ 5 }\) बन जाती है, जबकि अंश व हर दोनों में से यदि 5 घटाते हैं तो वह \(\frac { 1 }{ 2 }\) हो जाती है। भिन्न ज्ञात कीजिए।
हल

![]()
प्रश्न 10.
5 वर्ष पूर्व गीता की आयु कमला की आयु की 3 गुना थी। 10 वर्ष बाद गीता की आयु कमला की आयु की 2 गुना होगी। दोनों की वर्तमान आयु ज्ञात कीजिए।
हल
माना गीता की(RBSESolutions.com)वर्तमान आयु x वर्ष तथा कमला की वर्तमान आयु y वर्ष है।
प्रथम शर्तानुसार, (x – 5) = 3 (y – 5)
⇒ x – 6 = 3y – 15
⇒ x – 3y = -15 + 5
⇒ x – 3y = -10 …(i)
तथा द्वितीय शर्तानुसार,
(x + 10) = 2 (y + 10)
⇒ x + 10 = 2y + 20
⇒ x – 2y = 20 – 10
⇒ x – 2y = 10 …(ii)
समीकरण (i) में से (ii) घटाने पर
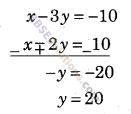
y का मान समीकरण (i) में रखने पर
x – 3 × 20 = -10
⇒ x = -10 + 60 = 50
अतः गीता की वर्तमान उम्र 50 वर्ष तथा कमला की वर्तमान उम्र 20 वर्ष है।
![]()
प्रश्न 11.
एक व्यक्ति 370 किमी की यात्रा में से कुछ दूरी रेल द्वारा तथा कुछ दूरी कार द्वारा तय(RBSESolutions.com)करता है। यदि वह 250 किमी रेल द्वारा तथा शेष दूरी कार द्वारा तय करता है, तो उसे 4 घण्टे लगते है। परन्तु जब वह 130 किमी रेल द्वारा तथा शेष दूरी कार द्वारा तय करता है तो उसे 18 मिनट अधिक लगते हैं। रेल तथा कार की चाल ज्ञात कीजिए।
हल
माना रेल की चाल x किमी/घंटा तथा कार की चाल y किमी/घंटा है।
जब वह 250 किमी ट्रेन द्वारा तय करता है तो उसे 370 – 250 = 120 किमी कार से तय करता है।


![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.4, drop a comment below and we will get back to you at the earliest.