RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Miscellaneous Exercise.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | Linear Equations in Two Variables |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 22 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Miscellaneous Exercise
Multiple Choice Questions
Question 1.
If y = 2x – 3 and y = 5 then value of x is:
(A) 1
(B) 2
(C) 3
(D) 4
Question 2.
If 2x + y = 6 then ordered pair (RBSESolutions.com) satisfying this equation is:
(A) (1, 2)
(B) (2, 1)
(C) (2, 2)
(D) (1, 1)
Question 3.
If \(\frac { 4 }{ x }\) + 5y = 7 and x = \(\frac { -4 }{ 3 }\) then value of y is:
(A) \(\frac { 37 }{ 15 }\)
(B) 2
(C) \(\frac { 1 }{ 2 }\)
(D) \(\frac { 1 }{ 3 }\)
![]()
Question 4.
If \(\frac { 3 }{ x }\) + 4y = 5 and y = 1 then value of x is:
(A) 3
(B) \(\frac { 1 }{ 3 }\)
(C) -3
(D) \(\frac { -1 }{ 3 }\)
Question 5.
If x = 1. then the value of y in the (RBSESolutions.com) equation \(\frac { 4 }{ x } +\frac { 3 }{ y } =5\) is:
(A) 1
(B) \(\frac { 1 }{ 3 }\)
(C) 3
(D) -3
Question 6.
If y and x are the digits in units place and tens place respectively then the number is:
(A) 10x + y
(B) 10y + x
(C) x + y
(D) xy
Question 7.
A boy is now one third as old as his mother. What will (RBSESolutions.com) be the age of the boy after 12 years if mother’s present age is x?
(A) \(\frac { x }{ 3 }\) + 12
(B) \(\frac { x+12 }{ 2 }\)
(C) x + 4
(D) \(\frac { x }{ 3 }\) – 12
Question 8.
The point on the x axis is:
(A) (2, 3)
(B) (2, 0)
(C) (0, 2)
(D) (2, 2)
Question 9.
Co-ordinates of (RBSESolutions.com) the origin are:
(A) (0, 0)
(B) (0, 1)
(C) (1, 0)
(D) (1, 1)
Question 10.
The point (3, -4) lies in the quadrant:
(A) first
(B) second
(C) third
(D) fourth
Answers
1. D
2. C
3. B
4. A
5. C
6. A
7. A
8. B
9. A
10. D
![]()
Question 11.
Express y in terms of x in 5y – 3x – 10 = 0. Also find the (RBSESolutions.com) point where the line 5y – 3x – 10 = 0 intersect the y-axis.
Solution.
The given equation is
5y – 3x – 10 = 0
Expressing y in terms of x, we get
5y = 3x + 10 ⇒ y = \(\frac { 3 }{ 5 }\)x + 2
Line will intersect y-axis if x = 0 3
⇒ y = \(\frac { 3 }{ 5 }\) x 0 + 2 ⇒ y = 2
Co-ordinate of the point is (0, 2) where the line will intersect y-axis.
Question 12.
By taking the values of x = -2 to x = 2 and also (RBSESolutions.com) included value of x for the equation y = 2x + 1. Form the table and draw the graph of the equation.
Solution.
The given equation is y = 2x + 1
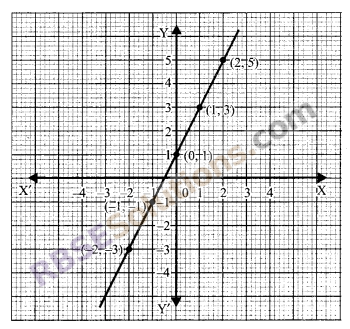
When x = -2
y = 2 x (-2) + 1 = -3
When x = -1
y = 2 x (-1) + 1 = – 2 + 1 = -1
When x = 0
y = 2 x 0 + 1 = 1
When x = 1
y = 2 x 1 + 1 = 3
When x = 2
y = 2 x 2 + 1 = 5
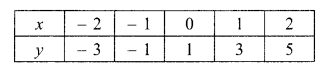
Question 13.
Solve the following (RBSESolutions.com) simultaneous equations
0.5x + 0.6y = 2.3
0.2x + 0.7y = 2.3
Solution.
The given equations are
0.5x + 0.6y = 2.3 ..(i)
0.2x + 0.7y = 2.3 …(ii)
Multiplying equation (i), by 2 and (ii) by 5 and then subtracting, we get
-2.3y = -6.9 ⇒ y = 3
Putting y = 3 in (i), we get
0.5x + 0.6 x 3 = 2.3
⇒ 0.5x + 1.8 = 2.3
⇒ 0.5x = 2.3 – 1.8
⇒ 0.5x = 0.5
⇒ x = 1
Hence the required solution is x = 1, y = 3.
Question 14.
Solve the following (RBSESolutions.com) system of equations
2x + 3y = 9
3x + 4y = 5
Solution.
The given equations are
2x + 3y = 9 …(i)
and 3x + 4y = 5 …(ii)
Multiplying equation (i) by 3 and (ii) by 2 and then subtracting, we get
y = 17
Putting the value of y = 17 in equation (i), we get
2x + 3 x 17 = 9
⇒ 2x + 51 = 9
⇒ 2x = 9 – 51
⇒ 2x = -42
⇒ x = -21
Hence the required solution is x = -21 and y = 17.
![]()
Question 15.
Solve the following (RBSESolutions.com) system of equations
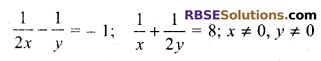
Solution.
The given system of equations are

Question 16.
Two numbers are such that if 7 is added to the (RBSESolutions.com) smaller number, then the sum is twice the greater and if 4 is added to the greater number, then the sum is thrice the smaller number. Find the two numbers.
Solution.
Let two numbers are x and y, where x > y
y + 7 = 2x
or 2x – y = 7 …(i)
also x + 4 = 3y
or x – 3y = – 4 …(ii)
Multiplying equation (ii) by 2 and then subtracting from (i), we get
5y = 15 ⇒ y = 3
Now substituting the (RBSESolutions.com) value of y in (i), we get
2x – 3 = 7
or 2x = 10
or x = 5
Hence, required numbers are 5 and 3.
Question 17.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and the denominator is increased by 1, then the denominator is eight times the (RBSESolutions.com) numerator. Find the fraction.
Solution.

![]()
Question 18.
5 books and 7 pens together cost ₹ 79, whereas 7 books and 5 pens (RBSESolutions.com) together cost ₹ 77. Find the total cost of 1 book and 2 pens.
Solution.
Suppose the cost of 1 book is ₹ x and the cost of 1 pen is ₹ y.
According to question
5x + 7y = 79
⇒ 5x + 7y – 79 = 0 ….(i)
and 7x + 5y = 11
⇒ 7x + 5y – 11 = 0 ….(ii)
Solving (i) and (ii), we get
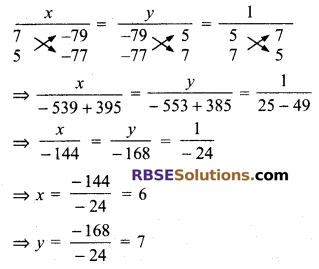
Therefore, cost of 1 book and 2 pens = 6 + 2 x 7 = 6 + 14 = ₹ 20.
Question 19.
When a number consisting of two digits is (RBSESolutions.com) multiplied by 9, it becomes equal to twice the number obtained by reversing the digits of the original number. If the difference of two digits of the number is 7, find the number.
Solution.
Let a two digit number be 10x + y in which x is tens place digit whereas y is units place digit.
According to question
9(10x +y) = 2(10y + x)
⇒ 90x + 9y = 20y + 2x
⇒ 88x = 11y
⇒ 8x – y = 0 …(i)
and x – y = -7 …(ii) [∴ Reject +ve value]
Solving (i) and (ii), we get x = 1 and y = 8
Hence, required number is 10x + y = 10 x 1 + 8 = 18
Question 20.
In a ∆ABC, ∠A = x°, ∠B = 3x° and ∠C = y°. If 5x – 3y + 30 = 0, then prove that it is a right angled triangle.
Solution.
Since it is given that
∠A = x°, ∠B = 3x° and ∠C = y°.
∠A + ∠B + ∠C = 180° (by angle sum (RBSESolutions.com) property of a triangle)
⇒ x + 3x + y = 180°
⇒ 4x + y = 180° …..(i)
Also 5x – 3y + 30 = 0
⇒ 5x – 3y = -30 …(ii)
Multiply equation (i) by 3 to make coefficient of y equal and then adding with (ii), we get
17x = 510 ⇒ x = 30°
Now putting the value of x in equation (i), we get
4 x 30° + y – 180°
or y = 180° – 120°
or y = 60°
Sum of two angles x and y is 90°
Hence, it is a right angled triangle.
![]()
Question 21.
Solve the following pair (RBSESolutions.com) of equations graphically.
(i) x + y = 4; x = y
(ii) x + y = 3; 2x + 5y = 12
(iii) 2x – 3y – 6 = 0; 2x + y + 10 = 0
(iv) 2x + y – 3 = 0; 2x – 3y – 7 = 0
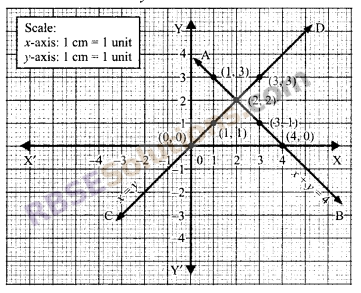
Solution.
(i) x + y = 4
⇒ y = 4 – x ……(i)
when x = 1, y = 3
when x = 2, y = 2
when x = 3, y = 1
when x = 4, y = 0
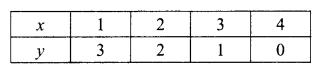
Plot the above ordered pairs (1, 3), (2, 2), (3, 1) and (4, 0) on the graph paper, join them (RBSESolutions.com) and get the graph AB (Line segment) and x = y
when x = 0, y = 0
x = 1, y = 1
x = 2, y = 2
x = 3, y = 3
Plot the points (1, 1), (2, 2), (0, 0) and (3, 3) on the same graph paper, join them and the get graph CD (Line segment)
The point of intersection of AB and CD is (2, 2)
Hence, required solution is x = 2, y = 2.
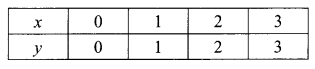
(ii) Given, x + y = 3
⇒ y = 3 – x
when x = 0, y = 3 – 0 = 3
when x = 3, y = 3 – 3 = 0
when x = 2, y = 3 – 2 = 1
Thus, we have the following table:
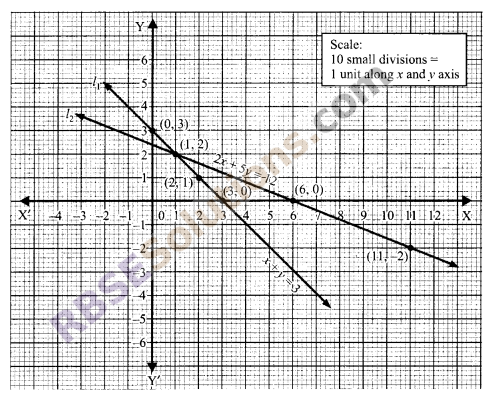
Now, plot the points (0, 3), (3, 0) and (2, 1) on a graph paper. Join (RBSESolutions.com) these points and extend the line l1 on both sides to obtain the graph of x + y = 3.
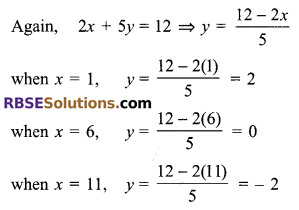
Thus, we have the following table:
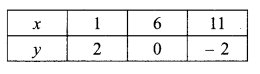
Now, plot the points (1, 2), (6, 0) and (11, – 2) on the same graph paper. Join these (RBSESolutions.com) points and extend the line l2 on both sides to obtain the graph of 2x + 5y = 12.
From the graph of the two equations, we see that lines l1 and l2 intersect and the coordinates of the point of intersection are (1, 2).
Hence, we say that x = 1, y = 2 is the only solution of the given system of equations.
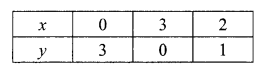
(iii) From equation
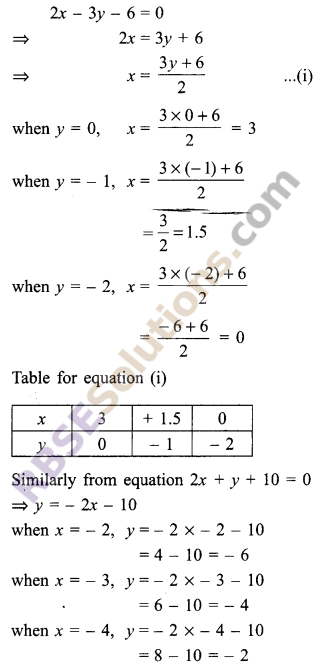
Table for Equation (ii)
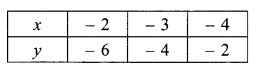
Now plotting and joining the points from table (i) and (ii) we find that (RBSESolutions.com) the lines are intersecting at a point (-3, -4).
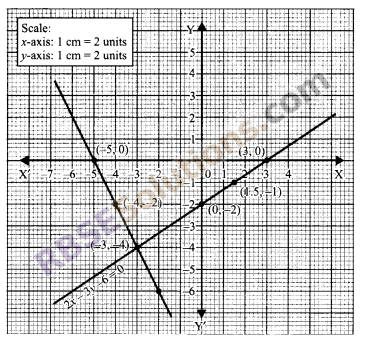
Hence, the required (RBSESolutions.com) solution is (- 3, – 4).
(iv) From equation 2x + y – 3 = 0
⇒ y = -2x + 3 …(i)
when x = 0, y = -2 x 0 + 3 = 3
when x = 1, y = -2 x 1 + 3 = 1
when x = 2, y = -2 x 2 + 3 = -1
Table for equation (i)


Now plotting and joining the points from the table (i) and (ii) on the same (RBSESolutions.com) graph paper, we find that their point of intersection is (2, -1). Hence the required solution is (2, -1).
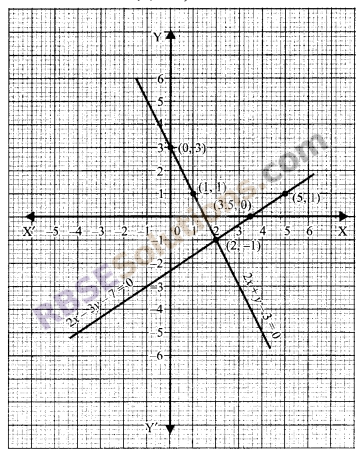
![]()
Question 22.
Solve the following system (RBSESolutions.com) of equations 2x – y = 1 and x + 2y = 8 graphically. Also, write the co-ordinate of the point where these lines intersect the y-axis.
Solution.
The given equations are
2x – y = 1
and x + 2y = 8
From equation (i)
2x – y = 1
⇒ y = 2x – 1
when x = 0, y = 2 x 0 – 1 = -1
when x = 1, y = 2 x 1 – 1 = 1
when x = 2, y = 2 x 2 – 1 = 3

Now plotting and joining the points from (RBSESolutions.com) the table (i) and (ii) on the same graph paper. We find that their points of intersection are (2, 3).
Hence the required solution is (2, 3). The above lines are intersecting y-axis at (0, – 1) and (0, 4) respectively.
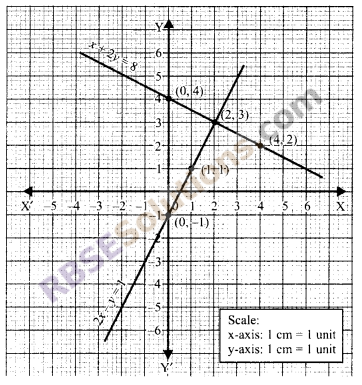
Hence the required solution is (2, 3). The above lines (RBSESolutions.com) are intersecting y-axis at (0, -1) and (0, 4) respectively.
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.