RBSE Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Additional Questions.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Plane Geometry and Line and Angle |
| Exercise | Additional Questions |
| Number of Questions Solved | 24 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Additional Questions
Multiple Choice Questions
Question 1.
In the figure, PQ || RS, ∠QPR = 70°, ∠ROT = 20° then the (RBSESolutions.com) value of x is:
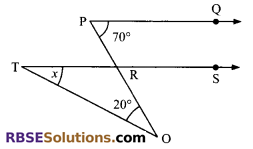
(A) 20°
(B) 70°
(C) 110°
(D) 50°
Solution:
D
Question 2.
Two angles measures (30 – a)° and (125 + 2a)°. If each one is the (RBSESolutions.com) supplement of the other, then ‘a’ is:
(A) 35°
(B) 25°
(C) 65°
(D) 45°
Solution:
B
![]()
Question 3.
In the given figure, if ∠COA = 62°, then x is:
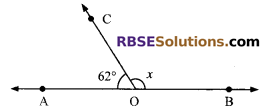
(A) 108°
(B) 128°
(C) 118°
(D) 32°
Solution:
C
Question 4.
The value of the variable (in the given figure) is (RBSESolutions.com) equal to:
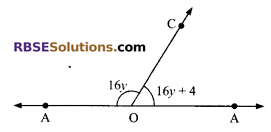
(A) 6
(B) 7
(C) 8
(D) 9
Solution:
C
Question 5.
In the given figure, what (RBSESolutions.com) value of x would make AOB a straight line?
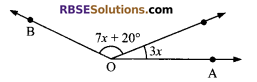
(A) 12°
(B) 14°
(C) 16°
(D) 18°
Solution:
C
Question 6.
In the given figure, the value of y is:
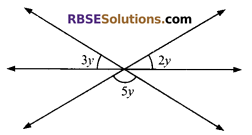
(A) 9°
(B) 18°
(C) 36°
(D) 54°
Solution:
B
Question 7.
In the given figure, if l || m then the (RBSESolutions.com) value of x is:
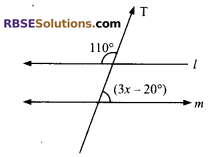
(A) 30°
(B) 40°
(C) 35°
(D) 45°
Solution:
A
Question 8.
In the given figure, if AB || CD, then the (RBSESolutions.com) value of x is:
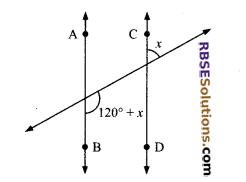
(A) 30°
(B) 20°
(C) 60°
(D) 45°
Solution:
A
Question 9.
In the given figure, the (RBSESolutions.com) value of x is equal to:
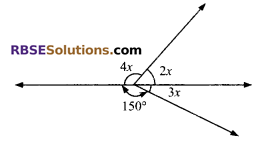
(A) 25°
(B) 30°
(C) 20°
(D) 40°
Solution:
B
![]()
Very Short Answer Type Questions
Question 1.
If the angles (3x – 20)° and (2x – 40)° are complementary angles. Find x.
Solution.
As we know that sum of the measure of (RBSESolutions.com) an angle and its complement is equal to 90°
(3x – 20)° + (2x – 40)° = 90°
⇒ 5x – 60° = 90°
⇒ 5x = 150°
⇒ x = 30°
Question 2.
An angle is 25° less than its complement. What is its measure?
Solution.
Let an angle be x
Its complement = 90° – x
According to question
x = 90° – x – 25°
⇒ 2x = 65°
⇒ x = 32\(\frac { { 1 }^{ 0 } }{ 2 }\)
Hence, measurement of the required angle be 32\(\frac { { 1 }^{ 0 } }{ 2 }\).
Question 3.
In the given figure, POS is a line, find (RBSESolutions.com) the measure of ∠QOR.
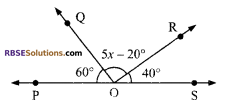
Solution.
Here we are given that POS is a straight line
∠POQ + ∠QOR + ∠ROS = 180° (straight angle)
⇒ 60° + 5x – 20° + 40° = 180°
⇒ 5x + 80° = 180°
⇒ 5x = 100°
⇒ x = 20°
∠QOR = 5x – 20° = 5 x 20° – 20° = 80°
Question 4.
In the given figure, if ∠1 + ∠2 = 100°, then (RBSESolutions.com) find the measure of ∠4.
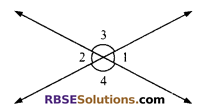
Solution.
∠1 + ∠2 = 100° (given)
But ∠1 = ∠2 (vertically opposite angles)
⇒ 2∠2 = 100°
⇒ ∠2 = 50°
Also ∠2 + ∠4 = 180° (linear pair)
⇒ ∠4 = 180° – 50° = 130°
Question 5.
In the given figure, (RBSESolutions.com) find the value of x.
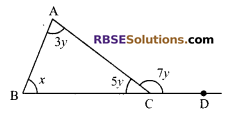
Solution.
Here ∠ACB + ∠ACD = 180° (Linear pair of angles)
⇒ 5x + 7y = 180°
⇒ 12y = 180°
⇒ y = 15°
Also x + 3y = 7y (Exterior angle property)
⇒ x = 4y
x = 4 x 15° ⇒ x = 60°
![]()
Question 6.
In the given (RBSESolutions.com) figure, find x and also find ∠POS.
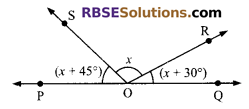
Solution.
∠POS + ∠SOR + ∠ROQ = 180° (Straight angle)
(x + 45°) + x + (x + 30°) = 180°
⇒ 3x + 75° = 180°
⇒ 3x = 105°
⇒ x = 35°
∠POS = (x + 45°) = (35° + 45°) = 80°
Question 7.
In the given figure, if lines EF || GH, then find (RBSESolutions.com) the value of x.
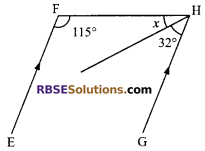
Solution.
EF || GH
115° + (x + 32°)= 180° (The sum of the interior angles on the same side of a transversal is supplementary)
⇒ x + 147° = 180°
⇒ x = 180° – 147° = 33°
Question 8.
In the figure, ∠POM and ∠QOM form (RBSESolutions.com) a linear pair. If x – 2y = 30°, find x and y.
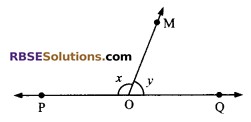
Solution.
∠POM and ∠QOM form a linear pair.
x + y = 180° …(i)
Also x – 2y = 30° (given) …(ii)
Solving (i) and (ii), we get x = 130° and y = 50°
Question 9.
In the figure, a : b : c = 4 : 3 : 5. If AOB is a straight line, find the (RBSESolutions.com) value of a, b and c.
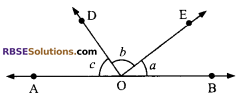
Solution.
We have, a : b : c = 4 : 3 : 5
⇒ ∠a = 4x, ∠b = 3x and ∠c = 5x
But ∠a + ∠b + ∠c = 180° (Straight angle)
⇒ 4x + 3x + 5x = 180°
⇒ 12x = 180°
⇒ x = 15°
Angles are 4 x 15° = 60°, 3 x 15° = 45° and 5 x 15° = 75°
Question 10.
If ray OC stands on line AB such that ∠AOC = ∠COB, then (RBSESolutions.com) show that ∠AOC = 90°.
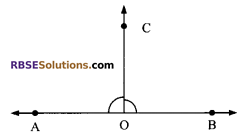
Solution.
Since ray OC stands on line AB. Therefore
∠AOC + ∠COB = 180° (Linear pair of angles)
But ∠AOC = ∠COB (given)
⇒ 2∠AOC = 180°
⇒ ∠AOC = 90°
![]()
Short Answer Type Questions
Question 1.
In the given figure, AC ⊥ AB. If ∠BAP = x, ∠PAQ = (x + 5°) and ∠CAQ = (2x + 5°), find the (RBSESolutions.com) value of x and reflex ∠PAQ.
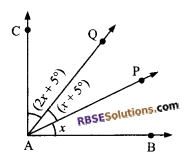
Solution.
We are given that AC ⊥ AB
⇒ ∠CAB = 90° (given)
⇒ ∠BAP + ∠PAQ + ∠CAQ = 90°
⇒ x + (x + 5°) + (2x + 5°) = 90°
⇒ 4x + 10° = 90°
⇒ 4x = 80°
⇒ x = 20°
⇒ ∠PAQ = (x + 5°) = 20° + 5° = 25°
Reflex ∠PAQ = 360° – 25° = 335°
Question 2.
In the given figure, AB || CD, if ∠OAB = 58° and ∠OCD = 45° then (RBSESolutions.com) find the value of x.
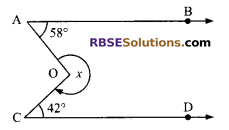
Solution.
We are given that AB || CD and ∠OAB = 58° and ∠OCD = 42°.
Construction: Draw a line PQ || AB || CD
To find: x
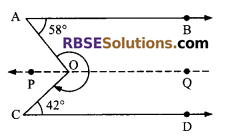
PQ || AB (by construction)
⇒ ∠AOP = ∠OAB = 58° (alternate angle)
∴ ∠COP = ∠OCD = 42° (alternate angle)
∴ ∠AOC = ∠AOP + ∠COP = 58° + 42°
⇒ ∠AOC = 100°
Thus, reflex ∠AOC
x = 360° – ∠AOC = 360° – 100° = 260°
Hence, x = 260°
Question 3.
In the figure, if EF || CD. Prove that AB || CD.
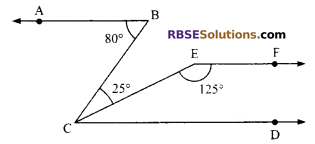
Solution.
We are given that EF || CD
EF || CD
∠FEC + ∠ECD = 180° (Sum of the interior angles (RBSESolutions.com) on the same side of a transversal is 180°)
⇒ 125° = ∠ECD = 180°
⇒ ∠ECD = 180° – 125° = 55°
⇒ ∠BCD = ∠BCE + ∠ECD = 25° + 25° = 80°
∠ABC = ∠BCD = 80°
These are alternate interior angles and they are equal.
Hence, AB || CD.
Question 4.
“If a transversal intersects two parallel lines, then each (RBSESolutions.com) pair of interior angles are supplementary”. Prove it.
Solution.
Given: AB and CD are two parallel lines and EF is a transversal which intersect them at M and N respectively forming two pairs of interior angles ∠1, ∠3 and ∠2, ∠4.
To Prove: (i) ∠1 + ∠3 = 180° or ∠2 + ∠4 = 180°
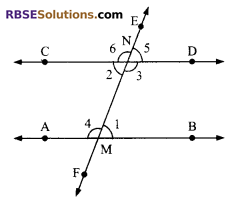
Proof: Since ray ND stands on line EF,
∠3 + ∠5 = 180° …(i) (linear pair of angles)
But ∠1 = ∠5 …(ii) (Corresponding angles as AB || CD)
From (i) and (ii), we get
∠1 + ∠3 = 180° …(iii)
Again ray CN stands on EF,
∠2 + ∠6 = 180° (Linear pair of angles)
But ∠4 = ∠6 (Corresponding angles as AB || CD)
⇒ ∠2 + ∠4 = 180° …(iv)
Hence, we can say if a transversal intersects two parallel lines, then (RBSESolutions.com) each pair of interior angles are supplementary
i.e. ∠1 + ∠3 = 180° or ∠2 + ∠4 = 180°
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Additional Questions, drop a comment below and we will get back to you at the earliest.