RBSE Solutions for Class 9 Maths Chapter 5 समतल ज्यामिती परिचय एवं रेखाएँ व कोण Ex 5.3

RBSE Solutions for Class 9 Maths Chapter 5 समतल ज्यामिती परिचय एवं रेखाएँ व कोण Ex 5.3 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 5 समतल ज्यामिती परिचय एवं रेखाएँ व कोण Exercise 5.3.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 9
Subject	Maths
Chapter	Chapter 5
Chapter Name	समतल ज्यामिती परिचय एवं रेखाएँ व कोण
Exercise	Exercise 5.3
Number of Questions Solved	10
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Maths Chapter 5 समतल ज्यामिती परिचय एवं रेखाएँ व कोण Ex 5.3

प्रश्न 1.
रेखाखण्ड AB = 10 सेमी खींचिए। इसका समद्विभाजन कीजिए तथा दोनों रेखा खण्डों को माप कर उत्तर की जाँच कीजिए।
हल
दिया है- रेखाखण्ड AB = 10 सेमी।
रचना करनी है- रेखाखण्ड AB का समद्विभाजन।
ज्ञात करना है- प्रत्येक भाग की माप।
रचना के पद

रेखाखण्ड AB = 10 सेमी खींचा।

परकार की सहायता से केन्द्र A तथा B से AB के आधे से अधिक लम्बाई की त्रिज्या लेकर AB के दोनों ओर चोप लगाये जो परस्पर C तथा D पर प्रतिच्छेद करते हैं।

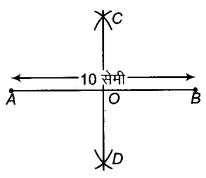
रेखा CD खींची जो AB को बिन्दु O पर काटती है।
अत: OA तथा OB समान लम्बाई के दो अभीष्ट रेखाखण्ड हैं।
माप : OA = OB = 5 सेमी।

प्रश्न 2.
120° के कोण की रचना कीजिए। इस कोण की समद्विभाजक रेखा खींचिए। दोनों कोणों को मापकर उत्तर की जाँच कीजिए।
हल
120° के कोण की रचना करना तथा इस कोण की समद्विभाजक रेखा खींचना।
रचना के पद

1. किरण OA खींची।
2. सुविधाजनक त्रिज्या लेकर केन्द्र 0 से चाप खींचा जो कि OA को बिन्दु P पर काटता हैं।
3. केन्द्र P से समान त्रिज्या से एक चाप लगाया जो कि पहले चाप को Q पर काटता हैं।
4. पुनः Q को केन्द्र मानकर उसी त्रिज्या(RBSESolutions.com)से चाप लगाया जो पद (2) वाली चाप को R पर काटता है।
5. OR को मिलाया तथा इसे आगे बिन्दु C तक बढ़ाया। इस प्रकार ∠AOB = 120° प्राप्त होता है।
   
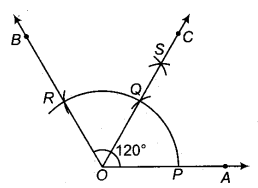
6. बिन्दु P तथा R को केन्द्र मानकर RP की आधे से अधिक त्रिज्या लेकर दो चाप लगाए, जो परस्पर बिन्दु S पर काटते हैं।
7. O तथा S को मिलाते हुए किरण OC खींची। अतः किरण OC, ∠AOB की समद्विभाजक रेखा है।
   नापने पर ∠AOC = ∠BOC = 60°

प्रश्न 3.
चाँदे की सहायता से 40° का कोण बनाइए। इसके बराबर कोण की रचना परकार तथा मापनी की सहायता से कीजिए।
हल
दिया है- माना ∠ABC = 40°
रचना करनी है- ∠ABC के बराबर ∠QRS की।
रचना के पद

1. सर्वप्रथम चाँदे की(RBSESolutions.com)सहायता से ∠ABC = 40° खींचा।
2. सरल रेखा PQ खींची, इस पर कोई बिन्दु R लिया।
   
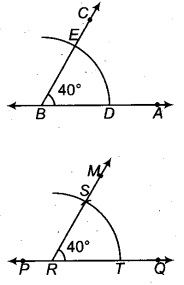
3. केन्द्र B से किसी त्रिज्या का चाप खींचा जो किरण BA और BC को क्रमशः D और E पर प्रतिच्छेद करता है।
4. केन्द्र R से भी उसी त्रिज्या (RT = BD) का चाप खींचा जो(RBSESolutions.com)रेखा P७ को बिन्दु T’ पर प्रतिच्छेद करता है।
5. रेखाखण्ड DE को नापा और केन्द्र T से त्रिज्या DE का एक चाप खींचा जो पद (4) में खींचे गए। चाप को बिन्दु S पर काटता है।
6. किरण RS खींची। ∠QRS अभीष्ट कोण है।3

प्रश्न 4.
एक 6 सेमी की रेखा खींचिए, इसके बाहर किसी। बिदु P से इस पर लम्ब खींचिए।
हल:
रचना के पद

1. AB = 6 सेमी का एक रेखाखण्ड खींचा। इसके बाहर कोई बिन्दु P लीजिए।
2. बिन्दु P से परकार की सहायता से सुविधाजनक त्रिज्या लेकर एक चाप लगाया जो रेखा AB को बिन्दु C और D पर काटता है।
   
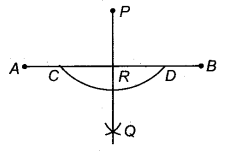
3. बिन्दु C और D को केन्द्र मानकर CD की आधी से अधिक त्रिज्या लेकर रेखाखण्ड AB के नीचे की ओर दो चाप लगाएँ। जो परस्पर. Q पर काटते हैं।
4. बिन्दु P को बिन्दु Q से मिलाया जो कि रेखाखण्ड AB को बिन्दु R पर काटता है। PR रेखाखण्ड AB पर लम्ब है।

प्रश्न 5.
∠ABC = 120° की रचना कीजिए। A से BC के समान्तर सरल रेखा खींचिए।
हल
रचना के पद

1. सुविधाजनक माप का एक रेखाखण्ड AB खींचा। AB के बिन्दु B से सुविधाजनक त्रिज्या लेकर एक चाप लगाया जो AB को बिन्दु P पर काटता है।
2. बिन्दु P को केन्द्र मानकर समान त्रिज्या(RBSESolutions.com)से चाप लगाया जो पहले चाप को बिन्दु Q पर काटता है।
3. बिन्दु Q को केन्द्र मानकर उसी त्रिज्या से चाप लगाया जो पद (1) वाले चाप को R पर काटता है।
4. B तथा R को मिलाते हुए रेखा BC खींची।
   
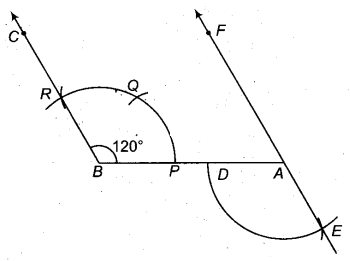
5. बिन्दु A को केन्द्र मानकर रेखा AB के नीचे की ओर पद (1) की त्रिज्या से चाप लगाया जो AB को D पर काटता है।
6. बिन्दु D को केन्द्र मानकर RP त्रिज्या(RBSESolutions.com)से चाप लगाया जो पद (5) वाले चाप को E पर काटता है।
7. EA को मिलाते हुए रेखा EF’ खींची AF’ रेखा BC के समान्तर रेखा है।

प्रश्न 6.
9 सेमी लम्बा एक रेखाखण्ड खींचिए। परकार व मापनी की सहायता से इसको तीन बराबर भागों में बांटिए।
हल
रचना के पद

1. AB = 9 सेमी का एक रेखाखण्ड खींचा।
   
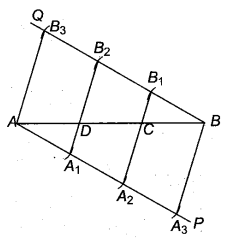
2. AB के दोनों 28, तरफ न्यूनकोण बनाती हुई क्रमशः दो रेखाएँ AP तथा BQ खींची।
3. AP रेखा पर समान त्रिज्या से तीन चाप इस प्रकार लगाते हैं कि AA₁ = A₁A₂ = A₂A₃
4. BQ रेखा पर समान त्रिज्या से तीन(RBSESolutions.com)चाप इस प्रकार लगाते हैं कि BB₁ = B₁B₂ = B₂B₃
5. A को B₃, A₁ को B₂, A₂ को B₁ तथा A₃ को B से मिलाया जो कि रेखाखण्ड AB को क्रमशः.D तथा C पर काटते हैं।
6. अतः AD, CD तथा BC रेखाखण्ड AB के तीन अभीष्ट भाग हैं।

प्रश्न 7.
10 सेमी लम्ब रेखा खण्ड खींचकर, परकार तथा मापनी की सहायता से इसको 3 : 2 भागों में बॉटिए। इनकी माप भी ज्ञात कीजिए।
हल
मानी AB एक रेखाखण्ड है जोकि 10 सेमी लम्बा है। इसको 3 : 2 में विभाजित करना है।
रचना के पद

1. सबसे पहले 10 सेमी. का रेखाखण्ड AB खींचा।
2. रेखाखण्ड AB के बिन्दु A से न्यूनकोण बनाती हुई एक किरण AX खींची।
   
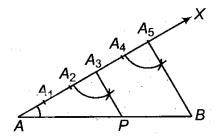
3. दिए हुए अनुपात (3 : 2) का योग 3 + 2 = 5 कर, किरण AX पर परकार की सहायता से बराबर दूरी के 5 भाग करके बिन्दु A₁, A₂, A₃, A₄ तथा A₅ अंकित करते हैं।
   अर्थात् AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ हों।
4. अन्तिम खण्ड (भाग) A5 को रेखाखण्ड AB के बिन्दु B से मिलाया(RBSESolutions.com)अर्थात् AB को मिलाया।
5. अब A5B के समान्तर A3P रेखा खींची (∠AA₅B = ∠AA₃P हों) जो AB रेखाखण्ड को P बिन्दु पर प्रतिच्छेद करती है, तब
   AP: PB = 3 : 2
   अत: रेखाखण्ड AB के AP और PB अभीष्ट भाग हैं। मापने पर- AP = 6 सेमी, PB = 4 सेमी

प्रश्न 8.
एक 6 सेमी लम्बा रेखा खण्ड AB खींचिए। परकार एवं पटरी की सहायता से इसको 1 : 2 : 3 भागों में बॉटिए।
हल
माना AB एक 6 सेमी लम्बा रेखाखण्ड है। जिसे 1 : 2 : 3 में बाँटना है।
रचना के पद-

1. सबसे पहले 6 सेमी नाप का रेखाखण्ड AB खींचा।
2. रेखाखण्ड AB के बिन्दु A से न्यूनकोण बनाती(RBSESolutions.com)हुई एक किरण AX खींची।
3. दिये हुए अनुपात (1 : 2 : 3) का. योग 1 + 2 + 3 = 6 कर, किरण AX पर परकार की सहायता से बराबर दूरी के 6 भाग करके बिन्दु A₁, A₂, A₃, A₄, A₅ और A₆ अंकित करते हैं।
   AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ हों।
   
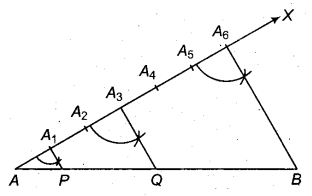
4. अंतिम भाग (A₆) को रेखाखण्ड A₆B के बिन्दु B से मिलाया अर्थात् AB को मिलाया।
5. अब A₆B के समान्तर A₃Q तथा A₁P खींची जो AB रेखाखण्ड को(RBSESolutions.com)क्रमशः Q तथा P बिन्दु पर प्रतिच्छेद करती है; तब AP : PQ : QB = 1 : 2 : 3
   अत: रेखाखण्ड AB के AP, PQ तथा QB अभीष्ट भाग हैं।

प्रश्न 9.
परकार और मापनी की सहायता से निम्न कोणों की रचना कीजिए- 45°, 75°, 105°, 150°
हल
45° के कोण की रचना
रचना के पद-

1. किरण OA खींची।
2. O को केन्द्र मानकर किसी भी सुविधाजनक त्रिज्या का एक चाप खींचा, जो OA को B बिन्दु पर काटता है।
   
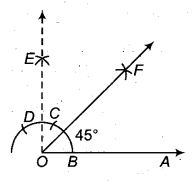
3. B को केन्द्र मानकर समान त्रिज्या से चाप खींचा जो पहले खींचे। चाप को C पर काटता है। फिर C केन्द्र से समान त्रिज्या, भरकर चाप खींचा जो पहले चाप को D पर काटता है।
4. C केन्द्र से CD की आधी से(RBSESolutions.com)अधिक त्रिज्या भरकर एक चाप खींचा।
5. D केन्द्र से समान त्रिज्या का दूसरा चाप लगाया जो पिछले चाप को E पर काटता है।
6. OE को मिलाया। इस प्रकार ∠AOE = 90° प्राप्त होता है।
7. ∠AOE का समद्विभाजक OF खींचा। इस प्रकार ∠AOF = 45° प्राप्त होता है।

75° के कोण की रचना
रचना करनी है- 75° के कोण की।

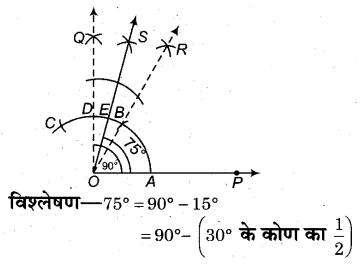
रचना के पद

1. किरण OP खींची, OP के बिन्दु O पर ∠POQ = 90° के कोण की रचना की।
2. B तथा D को केन्द्र मानकर(RBSESolutions.com)समान त्रिज्या से दो चाप लगाए जो परस्पर बिन्दु S पर काटते हैं। OS को मिलाया।
3. स्पष्ट है कि ∠POS = ∠POQ – ∠QOS = 90° – 15° = 75°
   अत: ∠POS अभीष्ट कोण है।

105° के कोण की रचना
रचना करनी है- 105° के कोण की।

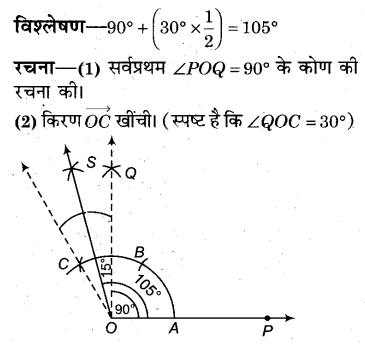
(3) ∠QOC का समद्विभाजक OS खींचा जिससे ∠QOS = 15°
इस प्रकार, ∠POS = 90° + 15° = 105° अभीष्ट कोण है।
150° के कोण की रचना

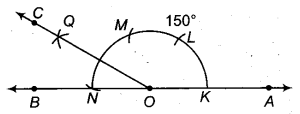
विश्लेषण- 150°= 60° + 60° + 30°
रचना के पद-

1. उचित माप का AB रेखाखण्ड खींचा। AB पर बिन्दु O लिया।
2. बिन्दु O से एक चाप लगाया। जो AB को K, तथा N पर काटता है।
3. बिन्दु K से उसी त्रिज्या से चाप(RBSESolutions.com)लगाया जो पहले चाप को L पर काटता है।
4. L को केन्द्र मानकर फिर उसी त्रिज्या से चाप लगाया जो पहले चापे को M पर काटता है।
5. M तथा N को केन्द्र मानकर MN के आधे से अधिक त्रिज्या से दो चाप लगाए जो एक दूसरे को Q पर काटते हैं।
6. O को Q से मिलाती हुई किरण OC खींची।
   इस प्रकार, ∠QOA = 150° का अभीष्ट कोण है।

प्रश्न 10.
बिना चाँदे का उपयोग करके निम्न कोणों की रचना कीजिए।
(i) 12°
(ii) 20°
(iii) 80°
(iv) 100°
(v) 155°
(vi) 218°
(vii) 307°
(viii) 127°
इनकी जाँच चाँदे से कीजिए।
हल
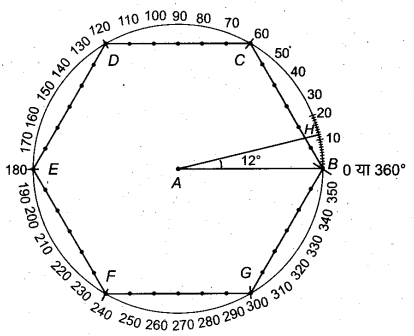
(i) 12° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की परिधि(RBSESolutions.com)पर पाँच चाप लगाते हैं, जो वृत्त को C, D, E, F’ व G पर काटता है।
4. BC, CD, DE, EF’, FG और GB को मिलाते हैं तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शून्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिये गये कोण का अवलोकन- 12° = 10° + 2° अतः रेखा BC पर या पहले खाने पर मिमी के चिह्न अंकित करते हैं और मिलीमीटर के 10 से आगे दूसरे चिह्न को A से मिलाते हैं। माना यह बिन्दु H है।
   इस प्रकार प्राप्त कोण ∠BAH = 12° ही अभीष्ट कोण होगा।
   
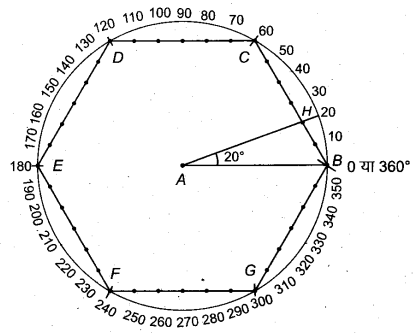
   चाँदे से जाँचने पर ∠BAH 12° का प्राप्त हुआ।

(ii) 20° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की परिधि पर पाँच चाप लगाते हैं, जो वृत्त को C, D, E, F’ व G पर काटते हैं।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं(RBSESolutions.com)तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शून्य लेते हुए सभी चिह्नों पर। संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिए गए कोण का अवलोकनदिया गया कोण = 20° = रेखा BC पर दूसरा चिह्न अत: BC रेखा पर दूसरे बिन्दु (माना, H) को A से मिलाते हैं। इस प्रकार प्राप्त कोण ∠BAH = 20° का होगा। यही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH = 20° पाया गया।

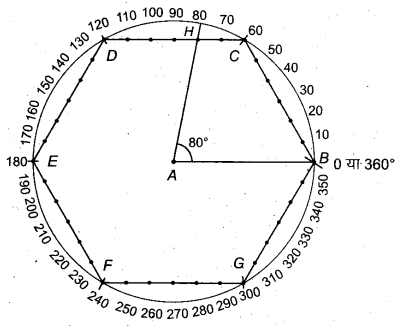
(iii) 80° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की परिधि पर पाँच चाप लगाते हैं, जो वृत्त को C, D, E, F’ व G पर काटता है।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं(RBSESolutions.com)तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शून्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिए गए कोण का अवलोकन
   दिया गया कोण = 80° = रेखा CD पर दूसरा चिह्न (माना, H)
   अतः CD रेखा पर दूसरे बिन्दु को A से मिलाते हैं। इस प्रकार प्राप्त ∠BAH = 80° का होगा। यही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH = 80° पाया गया।

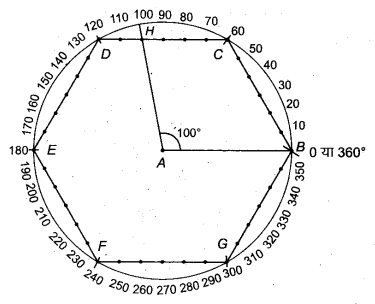
(iv) 100° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की(RBSESolutions.com)परिधि पर पाँच चाप लगाते हैं, जो वृत्त को C, D, E, F व.G पर काटती है।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शुन्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिए गए कोण का अवलोकनदिया गया कोण = 100° = रेखा CD पर चौथा चिह्न (माना, H)
   अतः CD रेखा पर चौथे बिन्दु को A से मिलाते हैं। इस प्रकार प्राप्त ∠BAH = 100° का होगा। यही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH 100° पाया गया।

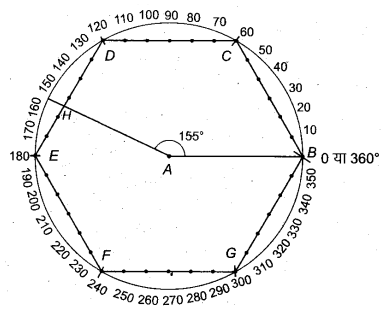
(v) 155° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्ते खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की(RBSESolutions.com)परिधि पर पाँच चाप लगाते हैं, जो वृत्त को C, D, E, F व G परे काटता है।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B का शून्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिए गए कोण का अवलोकन| दिया गया कोण = 155° = 150° + 5° अतः रेखा DE पर या तीसरे खाने पर मिमी के चिह्न अंकित करते हैं तथा पाँचवें चिह्न (माना, H) को A से मिलाते हैं। इस प्रकार प्राप्त कोण ∠BAH = 155° ही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH = 155° पाया गया।

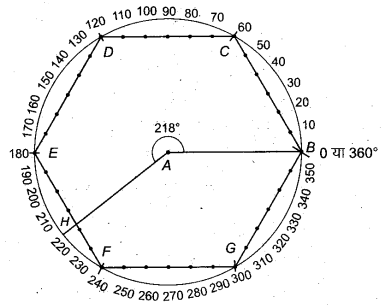
(vi) 218° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की परिधि पर पाँच चाप लगाते हैं, जो वृत्त को C, D, E, F’ व G पर काटता है।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं तथा(RBSESolutions.com)इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शून्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,….. अंकित करते हैं।
5. दिए गए कोण का अवलोकन
   दिया गया कोण = 218° = 210° + 8°
   अत: रेखा EF’ पर या चौथे खाने पर मिमी के चिह्न अंकित करते हैं तथा आठवें चिह्न (माना, H) को A से मिलाते हैं। इस प्रकार प्राप्त कोण ∠BAH = 218° ही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH = 218° पाया गया।

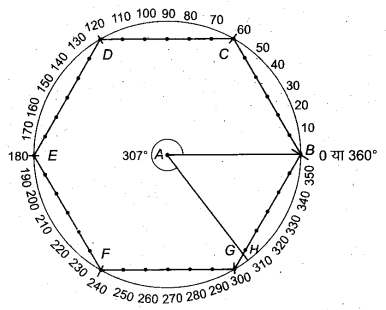
(vii) 307° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या को वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की परिधि पर पाँच(RBSESolutions.com)चाप लगाते हैं, जो वृत्त को C, D, E, F व G पर काटता है।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शून्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिए गए कोण का अवलोकन-
   दिया गया कोण = 307° = 300° + 7°
   अतः रेखा GB पर या छठे खाने पर मिमी के चिह्न अंकित करते हैं तथा सातवें चिह्न (माना, H) को A से मिलाते हैं। इस प्रकार प्राप्त कोण ∠BAH = 307° ही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH = 307° पाया गया।

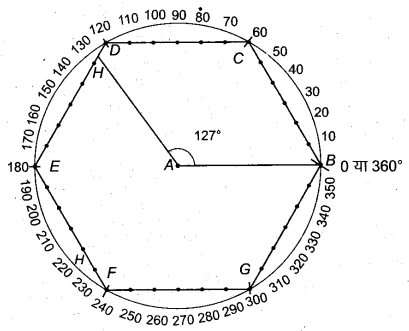
(viii) 127° के कोण की रचना

1. स्केल से 6 सेमी की सरल रेखा AB खींचो।
2. परकार से A को केन्द्र मानकर 6 सेमी त्रिज्या का वृत्त खींचो, जो B से होकर जाएगा।
3. परकार द्वारा इसी दूरी से वृत्त की परिधि पर पाँच चाप(RBSESolutions.com)लगाते हैं, जो वृत्त को C, D, E, F व G पर काटता है।
4. BC, CD, DE, EF, FG और GB को मिलाते हैं तथा इन पर स्केल से 1-1 सेमी पर चिह्न अंकित करते हैं। अब B को शून्य लेते हुए सभी चिह्नों पर संख्या 0, 10, 20, 30,…… अंकित करते हैं।
5. दिए गए कोण का अवलोकन
   दिया गया कोण = 127° = 120° + 7°
   अत: रेखा DE पर या तीसरे खाने पर मिमी. के चिह्न अंकित करते हैं तथा सातवें चिह्न (माना, H) को A से मिलाते हैं। इस प्रकार प्राप्त कोण ∠BAH = 127° ही अभीष्ट कोण है।
   
   चाँदे से जाँचने पर ∠BAH = 127° पाया गया।

We hope the given RBSE Solutions for Class 9 Maths Chapter 5 समतल ज्यामिती परिचय एवं रेखाएँ व कोण Ex 5.3 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 5 समतल ज्यामिती परिचय एवं रेखाएँ व कोण Exercise 5.3, drop a comment below and we will get back to you at the earliest.