RBSE Solutions for Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | सरल रेखीय आकृतियाँ |
| Exercise | Additional Questions |
| Number of Questions Solved | 24 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Additional Questions
अन्य महत्वपूर्ण प्रश्न
बहुविकल्पीय प्रश्न
प्रश्न 1.
त्रिभुज के तीनों कोणों का योगफल बराबर होता है
(A) एक समकोण के
(B) दो समकोण के
(C) तीन समकोण के
(D) चार समकोण के
प्रश्न 2.
समकोण त्रिभुज में सबसे बड़ा कोण हो सकता है-
(A) 180°
(B) \(\frac { 180 }{ 2 }\)
(C) \(\frac { 180 }{ 3 }\)
(D) \(\frac { 180 }{ 4 }\)
प्रश्न 3.
किसी भी त्रिभुज में कम से कम कितने कोण न्यूनकोण हो सकते हैं?
(A) एक
(B) दो
(C) तीन
(D) चार
![]()
प्रश्न 4.
चित्र में, x का मान होगा
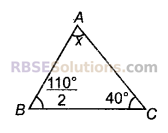
(A) 85°
(B) 75°
(C) 65°
(D) 95°
संकेत : x = 180° – 40° – \(\frac { 110 }{ 2 }\) = 140° – 55° = 85°
प्रश्न 5.
एक बहुभुज के सभी बहिष्कोणों का योग होता है।
(A) (2n – 4) × 180°
(B) 2 × 180°
(C) (n – 2) × 180°
(D) \(\frac { 360 }{ n }\)
![]()
प्रश्न 6.
चित्र में x को मान होगा-
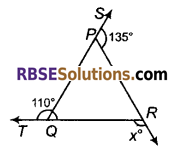
(A) 135°
(B) 125°
(C) 115°
(D) 105°
प्रश्न 7.
बहुभुज के लिए.n का मान क्या नहीं हो सकता है-
(A) n > 3
(B) n < 3
(C) n = 3
(D) n = ∞ (अनन्त)
प्रश्न 8.
बहुभुज में भुजाओं की संख्या बढ़ने पर आन्तरिक कोण का मान
(A) बढ़ता है
(B) घटता
(C) समान रहता है.
(D) इनमें से कोई नहीं
![]()
प्रश्न 9.
अष्टभुज में विकर्णो की संख्या होगी
(A) 10
(B) 20
(C) 30
(D) 40
प्रश्न 10.
दशभुज में अन्त:कोणों का योगफल होगा-
(A) 1440°
(B) 1430°
(C) 1420°
(D) 410°
उत्तरमाला
1. (B)
2. (B)
3. (C)
4. (A)
5. (B)
6. (C)
7. (B)
8. (A)
9. (B)
10. (A)
![]()
अतिलघूतटीय/लघूत्तीय प्रश्नोत्तर
प्रश्न 1.
क्या कोई ऐसा त्रिभुज संभव है, जिसमें दो कोण अधिककोण हों?
हल:
ऐसा त्रिभुज संभव नहीं है जिसमें दो कोण अधिक कोण हों, क्योंकि इस स्थिति में तीन कोणों का योग दो समकोण से अधिक हो जाएगा।
प्रश्न 2.
क्या कोई ऐसा त्रिभुज संभव है, जिसमें दो कोण न्यून कोण हों?
हल:
ऐसा त्रिभुज सम्भव है, जिसमें दो(RBSESolutions.com)कोण न्यूनकोण हों।
प्रश्न 3.
क्या कोई ऐसा त्रिभुज संभव है, जिसमें तीनों कोण 60° से अधिक हों?
हल:
ऐसी कोई त्रिभुज संभव नहीं है जिसमें सभी तीनों कोण 60° से अधिक हों। इस स्थिति में तीनों कोणों का योग 180° से अधिक हो जाएगा जबकि यह 180° के बराबर होना चाहिए।
![]()
प्रश्न 4.
क्या कोई ऐसा त्रिभुज संभव है, जिसमें तीनों कोण 60° के हों?
हल:
हाँ, ऐसा त्रिभुज सम्भव है, जिसमें तीनों कोण 60° के हों।
प्रश्न 5.
क्या कोई ऐसा त्रिभुज संभव है, जिसमें तीनों कोण 60° से कम के हो?
हल:
ऐसा त्रिभुज संभव नहीं है, जिसमें तीनों(RBSESolutions.com)कोण 60° से कम हों। ऐसी स्थिति में त्रिभुज के तीनों कोणों का योग 180° से कम होगा, जबकि यह 180° के बराबर होना चाहिए।
प्रश्न 6.
(a) किसी समबहुभुज में कम-से-कम कितने अंश का अन्त:कोण सम्भव है? क्यों?
(b) किसी समबहुभुज में अधिक-से-अधिक कितने अंश का बाह्य कोण सम्भव है?
हल:
(a) समबहुभुज में कम-से-कम 3 भुजाएँ होनी चाहिए। अतः कम-से-कम अंश का अन्त:कोण
= \(\frac { \left( 3-2 \right) \times { 180 }^{ 0 } }{ 3 } =\frac { 1\times { 180 }^{ 0 } }{ 3 }\) = 60°
अतः सम्भव अन्त:कोण = 60°
(b) कम-से-कम अंश(RBSESolutions.com)का अन्त:कोण = 60°
इसलिए, ज्यादा-से-ज्यादा अंश का बाह्य कोण = 180° – 60° = 120°
![]()
प्रश्न 7.
क्या इस आकृति में कोई त्रुटि है? टिप्पणी करें।
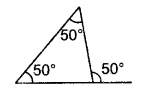
हल:
आकृति में बाह्य कोण अन्तः सम्मुख कोणों के योग के बराबर नहीं है।
अत: 50° ≠ 50° + 50°
अतः दिए गए कोण गलत है।
प्रश्न 8.
दिए गए चित्र में शेष कोणों के मान ज्ञात कीजिए। त्रिभुजों को नामांकित कीजिए, जहाँ ST || PQ
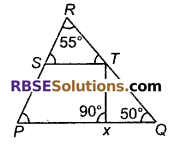
हल:
ΔPQR में,
∠P + ∠Q + ∠R = 180°
∠P + 50° + 55° = ∠P + 105° = 180°
∠P = ∠RST = ∠SPQ = 180° – 105° = 75° (संगत कोण)
इसी प्रकार, ∠RTS = ∠TQP = 50° (संगत कोण)
चित्र में तीन त्रिभुज हैं- ∆PQR, ∆RST व ∆TXQ
∆PQR के कोण हैं : 75°, 50° व 50°
अतः ∆PQR एक न्यूनकोण(RBSESolutions.com)त्रिभुज है।
∆RST के कोण हैं 55°, 75° व 50°
अत: ∆RST एक न्यूनंकोण त्रिभुज है।
∆TXQ का एक कोण ∠TXQ = 90° है।
अतः ∆TXQ एक समकोण त्रिभुज है।
![]()
प्रश्न 9.
आकृति में HOPE एक समान्तर चतुर्भुज है। x, y और z कोणों की माप ज्ञात कीजिए। ज्ञात करने में प्रयोग किए गए गुणों को बताईए।
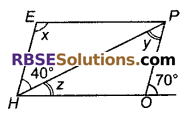
हल:
HOPE एक समान्तर चतुर्भुज है।
∠HOP = 180° – 70° = 110° (रैखिक कोण युग्म)
समान्तर चतुर्भुज के आसन्न(RBSESolutions.com)कोणों का योग 180° होता है।
अत: ∠EHO + ∠HOP = 180°
⇒ 40° + ∠z + 110° = ∠z + 150° = 180°
⇒ ∠z = 180° – 150° = 30°
अब पुन: ∠z + ∠y + ∠HOP = 180° [∵ ∆ के तीनों कोणों का योग 180° होता है।]
⇒ 30° + ∠y + 110° = 180°
⇒ 140° + ∠y = 180°
⇒ ∠y = 180° – 140° = 40°
अब, समान्तर चतुर्भुज के सम्मुख कोण बराबर होते है।
∠HEP = ∠HOP
∠x = 110°
![]()
प्रश्न 10.
किसी समान्तर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समान्तर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।

हल:
दिया है- दो आसन्न कोणों का अनुपात 3 : 2 है।
मानी दो(RBSESolutions.com)आसन्न कोण 3x तथा 2x हैं।
समान्तर चतुर्भुज के दो आसन्न कोणों का योग 180° होता है।
∠A + ∠B = 180°
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
अतः ∠A = 3x = 3 x 36° = 108°
तथा ∠B = 2x = 2 x 36° = 72°
समान्तर चतुर्भुज के सम्मुख कोण समान होते हैं।
अतः ∠C = ∠A = 108° तथा ∠D = ∠B = 72°
![]()
प्रश्न 11.
एक समबहुभुज की भुजाओं की संख्या ज्ञात कीजिए, यदि इसका प्रत्येक अन्तः कोण 165° का हो।
हल
माना एक समबहुभुज में भुजाओं की संख्या = n

प्रश्न 12.
किसी त्रिभुज के तीनों कोणों में 1 : 2 : 1 का अनुपात है। त्रिभुज के तीनों कोण ज्ञात कीजिए। त्रिभुज का दोनों प्रकार से वर्गीकरण भी कीजिए।
हल:
मानो त्रिभुज के कोण x, 2x और x है, तो
x + 2x + x = 180°
⇒ 4x = 180°
⇒ x = 45०
अतः त्रिभुज के कोण 45°, 90° वे 45° हैं।
अत: यह एक(RBSESolutions.com)समकोण समद्विबाहु त्रिभुज है।
![]()
प्रश्न 13.
दिए गए त्रिभुज में x का मान ज्ञात कर त्रिभुज को नामांकित कीजिए।
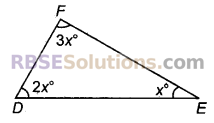
हल:
∆DEF में,
x° + 2x° + 3x° = 6x° = 180°
x° = 30°
∠E = x° = 30°, ∠D = 2x° = 60°, ∠F = 3x° = 90°
अत: ∆DEF’ एक समकोण त्रिभुज है।
प्रश्न 14.
नीचे दी गई आकृति में कोण x तथा y का मान ज्ञात कीजिए।
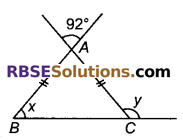
हल
∆ABC समद्विबाहु त्रिभुज है, जिसमें AB = AC
∠B = ∠C अर्थात् ∠B = ∠C = x
∠A = 92°, [शीर्षाभिमुख कोण]
त्रिभुज के तीनों कोणों का योग 180° होता है।
∠A + ∠B + ∠C = 180°
⇒ 92° + x + x = 180°
⇒ 2x = 180° – 92° = 88°
⇒ x = 44°
और ∠C + y = 180°, [रैखिक कोण युग्म]
y = 180° – 44° = 136° [∵ ∠C = x = 44°]
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Additional Questions, drop a comment below and we will get back to you at the earliest.