RBSE Solutions for Class 9 Maths Chapter 6 Rectilinear Figures Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 6 Rectilinear Figures Additional Questions.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Rectilinear Figures |
| Exercise | Additional Questions |
| Number of Questions Solved | 34 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 6 Rectilinear Figures Additional Questions
Multiple Choice Questions
Question 1.
The measure of an interior angle (RBSESolutions.com) of a regular pentagon is:
(A) 72°
(B) 108°
(C) 118°
(D) 540°
Solution:
(B) 108°
Question 2.
Each interior angle of a regular polygon measures 135°, then the polygon is:
(A) a parallelogram
(B) a hexagon
(C) an octagon
(D) a decagon
Solution:
(C) an octagon
Question 3.
The sum of all the interior (RBSESolutions.com) angles of a hexagon is:
(A) 5 right angles
(B) 6 right angles
(C) 8 right angles
(D) 12 right angles
Solution:
(C) 8 right angles
![]()
Question 4.
The sum of the exterior angles of a regular heptagon is:
(A) 180°
(B) 1080°
(C) 480°
(D) 360°
Solution:
(D) 360°
Question 5.
In a ∆PQR, if ∠P + ∠Q = ∠R then type (RBSESolutions.com) of triangle is:
(A) scalene triangle
(B) equilateral triangle
(C) isosceles triangle
(D) right-angled triangle
Solution:
(D) right-angled triangle
Question 6.
Every triangle must have at least two:
(A) acute angles
(B) obtuse angle
(C) right angles
(D) None of the above
Solution:
(A) acute angles
Question 7.
In a right angle triangle (RBSESolutions.com) one angle is 24°, then third angle will be:
(A) 66°
(B) 156°
(C) 114°
(D) None
Solution:
(A) 66°
Question 8.
Three angles of quadrilateral are 47°, 102° and 111°, then the fourth angle is equal to:
(A) 102°
(B) 100°
(C) 360°
(D) 260°
Solution:
(B) 100°
Question 9.
The number of diagonals in (RBSESolutions.com) a hexagon is equal to:
(A) 6
(B) 7
(C) 8
(D) 9
Solution:
(D) 9
Question 10.
In the adjoining figure, MN || BC. If ∠BAC = 80°, ∠CAN = 49°, then ∠ABC is equal to:
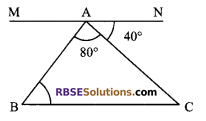
(A) 60°
(B) 50°
(C) 80°
(D) 40°
Solution:
(A) 60°
![]()
Very Short Answer Type Questions
Question 1.
In the given ∆ABC, the angle (RBSESolutions.com) bisectors of ∠B and ∠C meet at O. If ∠A = 70°, then find ∠BOC.
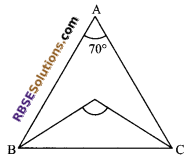
Solution.
As we know that
∠BOC = 90° + \(\frac { 1 }{ 2 }\) ∠A
= 90° + \(\frac { 1 }{ 2 }\) x 70°
= 90° + 35°
= 125°
Question 2.
Can a triangle have two right angles?
Solution.
No, if a triangle have two right angles, then sum (RBSESolutions.com) of two angles will be 180° which is not possible.
Question 3.
In the given figure, ∠ACD = 110°, ∠BAC = 45°, then find ∠ABC.
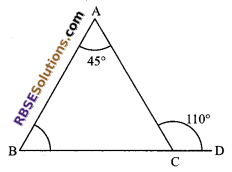
Solution.
∠A + ∠B = ∠ACD
Reason: ext. angle is equal to sum of opposite interior angles
∠B = 110° – 45° = 65°.
Question 4.
Determine the number of sides the polygon (RBSESolutions.com) for which the ratio of the sum of the interior angles to the sum of the exterior angle is 5 : 1.
Solution.
Suppose number of sides be n, then
\(\frac { sum of interior angles }{ sum of exterior angles }\) = \(\frac { 5 }{ 1 }\)
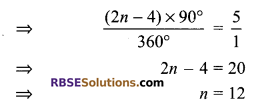
Question 5.
Evaluate x from the figure.
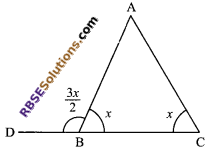
Solution.
\(\frac { 3x }{ 2 }\) + x = 180° (Linear pair axiom)
⇒ 5x = 360°
⇒ x = 72°
![]()
Question 6.
If a polygon has 10 sides. Find the (RBSESolutions.com) number of diagonals.
Solution.
No. of diagonals = \(\frac { 10(10-1) }{ 2 }\) – 10 = 45 – 10 = 35
Question 7.
State whether the following statement is true or false, give reason. The angles of a certain quadrilateral are 50°, 60°, 112°, 130°.
Solution.
Sum of the four angles of a quadrilateral is 50° + 60° + 112° + 130° = 352°
But sum of all the four angles of a quadrilateral is always 360°.
Hence given statement is false.
Question 8.
In any regular polygon interior angle is double (RBSESolutions.com) of exterior angle. Find the sides of the polygon.
Solution.
Suppose exterior angle be x Interior angle = 2x
⇒ x + 2x = 180°
⇒ 3x = 180°
⇒ x = 60°
sides = \(\frac { 360 }{ 60 }\) = 6
Question 9.
In one angle of a triangle is obtuse, what can you say about the remaining two angles.
Solution.
The other two angles must be acute.
Question 10.
In a triangle ABC, if ∠A = 58°, ∠B = 67°, then find ∠C.
Solution.
∠C = 180° – (58° + 67°) = 180° – 125° = 55°
Short Answer Type Questions
Question 1.
An exterior angle of a triangle is 110° and one (RBSESolutions.com) of the interior opposite angle is 30°. Find the other two angles of the triangle.
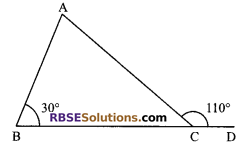
Solution.
In ∆ABC,
∠ACD = ∠ABC + ∠BAC
110° = 30° + ∠BAC
∠BAC = 80°
Now, ∠ACB = 180° – 110° = 70°
Question 2.
Two angles of a triangle are equal and (RBSESolutions.com) the third angle is greater than each of the equal angles by 21°. Find the measure of the angles.
Solution.
Let equal angles be x each and third angle = x + 21°
Then according to question, we have
x + x + (x + 21°) = 180° (angle sum property)
⇒ 3x + 21° = 180°
⇒ 3x = 159°
⇒ x = 53°
Measures of each angles are 53°, 53° and 74°.
![]()
Question 3.
Find the number of sides of (RBSESolutions.com) a polygon which has 14 diagonals.
Solution.
Number of diagonals of a polygon of n sides = \(\frac { n(n-1) }{ 2 }\) – n
⇒ 14 = \(\frac { n(n-1) }{ 2 }\) – n
⇒ 28 = n2 – n – 2n
⇒ n2 – 3n – 28 = 0
⇒ n2 – 7n + 4n – 28 = 0
⇒ n(n – 7) + 4(n – 7) = 0
⇒ (n – 7) (n + 4) = 0
⇒ n = 7
Question 4.
The sum of the base angles of a triangle is 130° and their difference is 40°. Find the measures of all its angles.
Solution.
Suppose base angles are B and C
According to problem
∠B + ∠C = 130° (given)
∠B – ∠C = 40° (given)
⇒ 2 ∠B = 170°
⇒ ∠B = 85°
∠C = 130° – 85° = 45°
Hence, ∠B = 85°, ∠C = 45° and ∠A = 50°.
Question 5.
In ΔPQR, if 2∠P = 3∠Q = 6∠R. calculate (RBSESolutions.com) measures of each of the angles.
Solution.
Let 2∠P = 3∠Q = 6∠R = x

Question 6.
In an isosceles triangle, the measure (RBSESolutions.com) of the greatest angle is 96°. Find the measure of each of the equal angles.
Solution.
According to question
x + x + 96° = 180° (by angle sum property of a triangle)
⇒ 2x + 96° = 180°
⇒ 2x = 84°
⇒ x = 42°
Measures of each equal angles of an isosceles triangle is 42°.
Question 7.
In figure, find ∠x, ∠y and ∠ACD where line BA || FE.
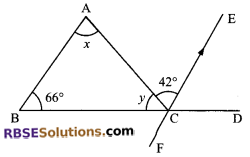
Solution.
BA || FE
∠x = 42° (alternate angle)
∠ACD = ∠x + 66° (ext. angle is equal to sum of opposite interior angles)
∠ACD = 42° + 66° = 108°
But ∠y + ∠ACD = 180°
∠y = 180° – 108° (linear pair axiom)
∠y = 72°
∠x = 42° and ∠y = 72°
Question 8.
The sum of two angles is 123° and their (RBSESolutions.com) difference is 13°. Find all the angles of the triangle.
Solution.
Let two angles are x and y, then according to question
∠x + ∠y = 123° …(i)
and ∠x – ∠y = 13° …(ii)
Adding (i) and (ii), we get
2∠x = 136° ⇒ ∠x = 68°
Now substituting ∠x = 68° in equation (i), we get
68° + ∠y = 123°
⇒ ∠y = 123° – 68° = 55°
Third angle = 180° – 123° = 57°
Hence angles of a triangle are 68°, 55°, 57°.
![]()
Question 9.
In ΔABC, ∠A = 2∠B and 2∠C = ∠A + ∠B. Find (RBSESolutions.com) the angles.
Solution.
∠A + ∠B + ∠C = 180° …(i) (by angle sum property of a triangle)
But ∠A + ∠B = 2∠C (given)
2∠C + ∠C = 180°
⇒ 3∠C = 180°
⇒ ∠C = 60°
From (i), ∠A + ∠B + 60° = 180°
⇒ ∠A + ∠B = 120°
But ∠A = 2 ∠B (given)
2∠B + ∠B = 120°
⇒ 3∠B = 120°
⇒ ∠B = 40°
∠A = 2 x 40 = 80°
Hence angles of a ΔABC are 80°, 40°, 60°.
Long Answer Type Questions
Question 1.
In a ΔABC the bisector of ∠ABC and ∠BCA intersect (RBSESolutions.com) at the point O. Prove that ∠BOC = 90° + ∠\(\frac { A }{ 2 }\).
Solution.
In ΔABC, we have
∠A + ∠B + ∠C = 180° (sum of the angles of a triangle)
⇒ \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B + \(\frac { 1 }{ 2 }\) ∠C = 90°
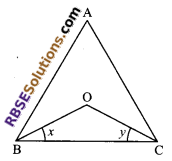
⇒ \(\frac { 1 }{ 2 }\) ∠A + ∠x + ∠y = 90° ….(i)
Again in ΔOBC
∠OBC + ∠OCB + ∠BOC = 180° (by angle sum property of a triangle)
⇒ ∠x + ∠y + ∠BOC = 180° …(ii)
Substituting ∠x + ∠y = 90° – \(\frac { 1 }{ 2 }\)∠A from (i) in eqn (ii), we get
90° – \(\frac { 1 }{ 2 }\) ∠A + ∠BOC = 180°
⇒ ∠BOC = 180° – 90° + \(\frac { 1 }{ 2 }\) ∠A
⇒ ∠BOC = 90° + \(\frac { 1 }{ 2 }\) ∠A
Hence proved.
Question 2.
Prove that the sum of the exterior angles of a triangle (RBSESolutions.com) formed by producing the sides of the triangle in order is equal to 4 right angles.
Solution.
In ΔABC,
∠y = ∠1 + ∠3 …(i) (due to ext. angle property)
and ∠z = ∠1 + ∠2 …(ii) (due to ext. angle property)
also ∠x = ∠2 + ∠3 …(iii) (due to ext. angle property)
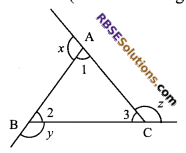
Adding equation (i), (ii) and (iii), we get
∠x + ∠y + ∠z = ∠1 + ∠3 + ∠1 + ∠2 + ∠2 + ∠3
⇒ ∠x + ∠y + ∠z = 2∠1 + 2∠2 + 2∠3
⇒ ∠x + ∠y + ∠z = 2(∠1 + ∠2 + ∠3) = 2 x 180° = 360°
Hence, ∠x + ∠y + ∠z = 4 right angles.
Question 3.
The exterior angle of a regular polygon is one-third (RBSESolutions.com) of its interior angle. How many sides has the polygon?
Solution.

![]()
Question 4.
In the figure, AO and BO are the bisectors (RBSESolutions.com) of two adjacent angles A and B of a quad. ABCD. Prove that 2∠AOB = ∠C + ∠D
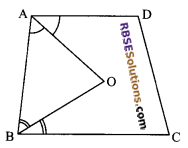
Solution.
Given: In quad. ABCD the bisectors of ∠A and ∠B intersect at O.
To prove: 2∠AOB = ∠C + ∠D
Proof: In quad. ABCD
∠A + ∠B + ∠C + ∠D = 360° …(i) (angle sum property of a quad.)
Also in ΔAOB
∠OAB + ∠OBA + ∠AOB = 180° (by angle sum property of a Δ)
⇒ \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B + ∠AOB = 180°
⇒ ∠A + ∠B + 2∠AOB = 360°…(ii)
From (i) and (ii), we get
∠A + ∠B + ∠C + ∠D = ∠A + ∠B + 2∠AOB
⇒ 2∠AOB = ∠C + ∠D
Hence proved.
Question 5.
In the figure, the side BC of ΔABC is produced to D. The (RBSESolutions.com) bisector of ∠A meets BC at P. Prove that: ∠ABC + ∠ACD = 2 ∠APC.
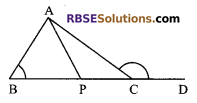
Solution.
Given: The side BC of ΔABC is produced to D.
The bisector of ∠A meets BC at P.
To prove: ∠ABC + ∠ACD = 2∠APC
Proof: ∠APC = ∠ABP + ∠BAP (the exterior angle is (RBSESolutions.com) equal to sum of opposite interior angles)
∠APC = ∠B + \(\frac { 1 }{ 2 }\) ∠A …(i)
Now in ΔABC
∠ABC + ∠BAC = ∠ACD …(ii) (reason as above)
Adding ∠ABC to both side of equation (ii), we get
∠ABC + ∠ACD = ∠ABC + ∠ABC + ∠BAC
= 2 ∠ABC + ∠BAC
= 2 ∠B + ∠A
= 2(∠B + \(\frac { 1 }{ 2 }\) ∠A)
= 2 ∠APC [from equation (i)]
∠ABC + ∠ACD = 2 ∠APC.
Hence proved.
We hope the given RBSE Solutions for Class 9 Maths Chapter 6 Rectilinear Figures Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 6 Rectilinear Figures Additional Questions, drop a comment below and we will get back to you at the earliest.