RBSE Solutions for Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Ex 6.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Exercise 6.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | सरल रेखीय आकृतियाँ |
| Exercise | Exercise 6.1 |
| Number of Questions Solved | 11 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Ex 6.1
प्रश्न 1.
दिए गए चित्र से, ΔABC के तीनों कोण ज्ञात कीजिए।
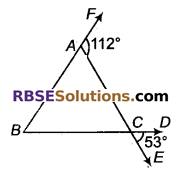
हल:
∠BAC = 180° – ∠CAF = 180° – 112° = 68°
∠BCA = 53° (शीर्षाभिमुख कोण)
ΔABC से,
∠ABC + ∠BCA + ∠BAC = 180°
⇒ ∠ABC + 53° + 68° = ∠ABC + 121° = 180°
⇒ ∠ABC = 180° – 121° = 59°
अत: त्रिभुज ABC के तीनों कोण 53°,59° व 68° हैं। (ZA = 68°, ZB = 59°, 20 = 53°)
![]()
प्रश्न 2.
चित्र में, ΔABC एक समबाहु त्रिभुज है। चित्र से ∠x, ∠y और ∠z के मान ज्ञात कीजिए।
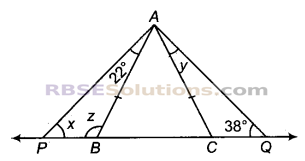
हल:
दिया है- ΔABC एक समबाहु त्रिभुज है।
∠ABC = ∠CAB = ∠BCA = 60°
⇒ ∠ABC + ∠ABP = 180° (रैखिक युग्म कोण)
⇒ ∠ABC + z = 180°
⇒ 60° + z = 180°
⇒ z = 180° – 60° = 120°
ΔABP में,
∠ABP + ∠BPA + ∠PAB = 180°
⇒ 120° + x + 22° = 180°
⇒ x = 180° – 142° = 38°
ΔAPQ में,
∠APQ + ∠PQA + ∠QAP = 180°
⇒ x + 38°+ (22° + y + ∠BAC) = 180°
⇒ 38° + 38° + 22° + y + 60° = 180°
⇒ y + 158°= 180°
⇒ y = 180° – 158° = 22°
अत: x = 38°, y = 22° व z = 120°
![]()
प्रश्न 3.
चित्र में ΔABC की भुजाएँ AB और AC को क्रमश: E और D तक बढ़ाया गया है। यदि ∠CBE और ∠BCD के समद्विभाजके क्रमशः BO और CO बिन्दु O पर मिलते हैं, तो सिद्ध कीजिए कि
∠BOC = 90° – \(\frac { \angle x }{ 2 }\) है।
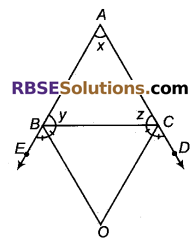
हल:
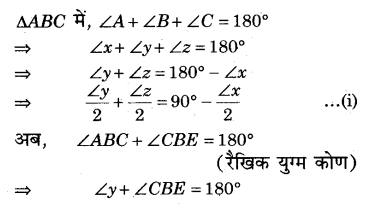

![]()
प्रश्न 4.
चित्र में, ∠P = 52° और ∠PQR = 64° है। यदि QO और RO क्रमशः ∠PQR और ∠PRQ के समद्विभाजक हैं, तो ∠x और ∠y के मान ज्ञात कीजिए।
हल:
दिया है- ∠P = 52°,
∠PQR = 64°
ΔPQR में,
∠P + ∠PQR + ∠QRP = 180°
⇒ 52° + 64° + ∠QRP = 116° + ∠QRP = 180°
⇒ ∠QRP = 180° – 116° = 64°
⇒ ∠y = \(\frac { 1 }{ 2 }\) ∠QRP = \(\frac { 1 }{ 2 }\) × 64° = 32°
ΔOQR में,
∠OQR + ∠QOR + ∠ORQ = 180°
⇒ 32° + ∠x + 32° = ∠x + 64° = 180° [∵ ∠OQR = ∠PQR, ∠ORQ = ∠y]
⇒ ∠x = 180° – 64° = 116°
![]()
प्रश्न 5.
चित्र में, यदि AB || DE, ∠BAC = 35° और ∠CDE = 53° है, तो ∠DCE ज्ञात कीजिए।
हल:
AB || DE
∠A = ∠E = 35° (एकान्तर कोण)
∠DCE + ∠D + ∠E = 180°
⇒ ∠DCE + 53° + 35°
⇒ ∠DCE + 88° = 180°
⇒ ∠DCE = 180° – 88° = 92°
![]()
प्रश्न 6.
चित्र में, यदि रेखाएँ PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती हैं। कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75° है तो ∠SQT का मान ज्ञात कीजिए।
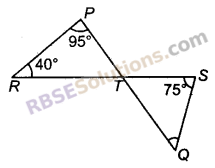
हल:
ΔPRT में,
∠PRT + ∠RTP + ∠TPR = 180° [त्रिभुज के तीनों कोणों का योग = 180°]
⇒ 40° + ∠RTP + 95° = 180°
⇒ ∠RTP = 180° – 40° – 95° = 45°
⇒ ∠STQ = ∠RTP (शीर्षाभिमुख कोण]
STQ = 45° [∵ ∠RTP = 45°]
ΔTQS में,
⇒ ∠SQT + ∠STQ + ∠TSQ = 180° [त्रिभुज के तीनों कोणों का योग = 180°]
⇒ ∠SQT’ + 45° + 75° = 180° [∵ ∠STQ = 45°]
⇒ ∠SQT = 180° – 45° – 75° = 60°
![]()
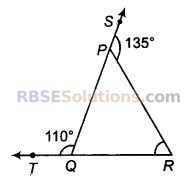
प्रश्न 7.
चित्र में, ΔPQR की भुजाओं QP और RQ को 135° क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR = 135° है और ∠PQT = 110° है, तो ∠PRQ ज्ञात कीजिए।

हल:
∠PQR = 180° – 110° = 70°
∠SPR = ∠PQR + ∠QRP (बहिष्कोण = अंन्तराभिमुख कोणों का योग)
⇒ 135°= 70° + ∠QRP
⇒ ∠QRP = 135° – 70° = 65°
![]()
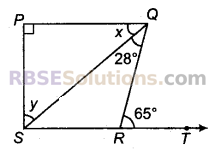
प्रश्न 8.
चित्र में, यदि PQ ⊥ PS, PQ || SR, ∠SQR = 28° और ∠QRT = 65° है, तो x और y के मान ज्ञात कीजिए।

हल:
ΔSRQ में बहिष्कोण प्रमेय गुण का उपयोग करते हुए, ∠QRT = ∠RQS + ∠QSR
65° = 28° + ∠QSR [∵ ∠QRT = 65°, ∠RQS = 28°]
∠QSR = 65° – 28° = 37°
अब PQ || SR तथा तिर्यक रेखा PS उनको क्रमशः P तथा S पर काटती है।
∠PQS = ∠QSB = 37° (एकान्तर कोण)
ΔPSQ में,
∠PSQ + ∠PQS + ∠SPQ = 180°
⇒ y + 37° + 90° = 180° [∠QSR = ∠SQP = 37°]
⇒ y = 180° – 90° – 37° = 53°
⇒ x = ∠PQS = 37°
![]()
प्रश्न 9.
चित्र में, ΔPQR की भुजा QR को बिन्दु S तक बढ़ाया गया है। यदि ∠PQR और ∠PRS के समद्विभाजक बिन्दु T पर मिलते हैं तो सिद्ध कीजिए कि ∠QTR = \(\frac { 1 }{ 2 }\) ∠QPR है।
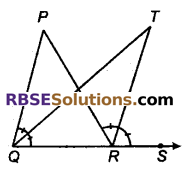
हल:
ΔPQR में,
बाह्य ∠PRS = ∠P + ∠Q
⇒ \(\frac { 1 }{ 2 }\) बाह्य ∠PRS = \(\frac { 1 }{ 2 }\) ∠P + \(\frac { 1 }{ 2 }\) ∠Q
⇒ ∠TRS = \(\frac { 1 }{ 2 }\) ∠P + ∠TQR …(i)
QT तथा RT क्रमश: ∠Q तथा ∠PRS के कोण समद्विभाजक हैं।
∠Q = 2∠TQR तथा बाह्य ∠PRS = 2∠TRS
ΔQRT’ में,
\(\frac { 1 }{ 2 }\) ∠TRS = ∠TQR + ∠T …(ii)
समीकरण (i) तथा (ii) से,
\(\frac { 1 }{ 2 }\) ∠P + ∠TQR = ∠TQR + ∠T
⇒ \(\frac { 1 }{ 2 }\) ∠P = ∠T
⇒ \(\frac { 1 }{ 2 }\) ∠QPR = ∠QTR
⇒ ∠QTR = \(\frac { 1 }{ 2 }\) ∠QPR
![]()
प्रश्न 10.
एक त्रिभुज ABC का कोण A समकोण है। BC पर एक बिन्दु L इस प्रकार है कि AL ⊥ BC है। सिद्ध कीजिए ∠BAL = ∠ACB
हल:
दिया है- ΔABC का कोण A समकोण है।
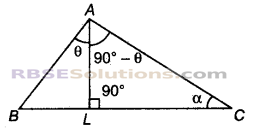
माना ∠BAL = θ तो
∠LAC = 90° – θ तथा ∠LCA = α
त्रिभुज के तीनों कोणों का योग 180° होता है।
ΔALC में,
∠LAC + ∠ACL + ∠CLA = 180°
⇒ (90° – θ) + α + 90° = 180°
⇒ 180° – θ + α = 180°
⇒ α = 180° – 180° + θ = θ
⇒ θ = α.
अतः ∠BAL = ∠ACB
इति सिद्धम्
![]()
प्रश्न 11.
किसी त्रिभुज के कोणों का अनुपात 2 : 3 : 4 है। इस त्रिभुज के तीनों कोण ज्ञात कीजिए।
हल:
त्रिभुज के तीनों कोणों का अनुपात = 2 : 3 : 4
माना त्रिभुज के तीनों कोण 2x°, 3x° तथा 4x° हैं।
2x° + 3x° + 4x° = 180°
⇒ 9x° = 180°
⇒ x° = 20°
तीन कोण = 2x°, 3x°, 4x°
= 2 × 20°, 3 × 20°, 4 × 20°
= 40°, 60°, 80°
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Ex 6.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Ex 6.1, drop a comment below and we will get back to you at the earliest.