RBSE Solutions for Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Ex 7.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Exercise 7.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 7 |
| Chapter Name | त्रिभुजों की सर्वांगसमता एवं असमिकाएँ |
| Exercise | Exercise 7.1 |
| Number of Questions Solved | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Ex 7.1
प्रश्न 1.
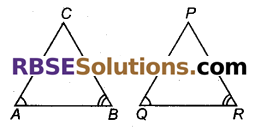
त्रिभुजों ABC और PQR में ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
हल:
∆PQR की भुजा QR, ∆ABC की भुजा AB के बराबर होगी क्योंकि दो त्रिभुज (RBSESolutions.com)होने के लिए एक त्रिभुज के दो संगत कोणों और उनकी अन्तरित भुजा दूसरे त्रिभुज के दो कोणों और उनकी अन्तरित संगत भुजा के बराबर होती है।
![]()
प्रश्न 2.
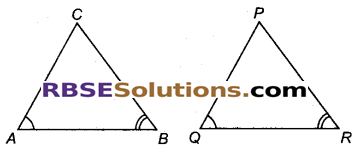
त्रिभुजों ABC और PQR में ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन-सी भुजा ∆ABC की भुजा BC के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
हल:
∆PQR में भुजा RP, ∆ABC की भुजा BC के बराबर होगी (RBSESolutions.com)दो त्रिभुज सर्वांगसम होने के लिए एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो संगत कोणों व संगत भुजा के बराबर होते हैं।
![]()
प्रश्न 3.
यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हो, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए। क्या यह कथन सत्य है? क्यों?
हल:
नहीं, यह कथन सत्य नहीं है। क्योंकि (RBSESolutions.com)होने के लिए कोण दोनों भुजाओं के अन्तर्गत होने चाहिए।
प्रश्न 4.
“यदि किसी त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों, तो त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।’ क्या यह कथन सत्य है? क्यों?
हल:
नहीं, यह कथन सत्य नहीं है।, क्योंकि भुजाएँ संगत होनी चाहिए।
![]()
प्रश्न 5.
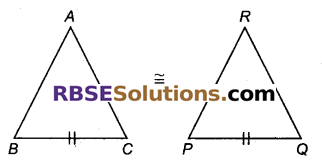
∆ABC = ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR है? क्यों?
हल:
नहीं, यह कथन सत्य नहीं है, क्योंकि QR, BC की संगत भुजा नहीं।
![]()
प्रश्न 6.
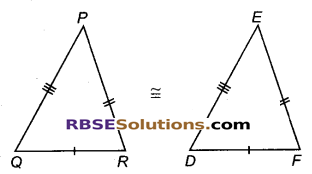
यदि ∆PQR = ∆EDF है, तो क्या यह कहना, सत्य है कि PR = EF है? अपने उत्तर के लिए कारण दीजिए।
हल:
हाँ, यह कथन सत्य है क्योंकि PR की संगत भुजा EF है।
![]()
प्रश्न 7.
चित्र में चतुर्भुज ABCD का विकर्ण AC शीर्ष कोण A एवं C का समद्विभाजक हो तो सिद्ध कीजिए: AB = AD एवं CB = CD
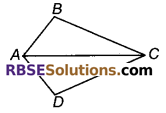
हल:
दिया है : चतुर्भुज ABCD, जहाँ AC, 2A व C को समद्विभाजक है।
सिद्ध करना है: AB = AD तथा CB = CD
उपपत्ति : ∠BAD = 2∠BAC = 2∠DAC
∠BAC = \(\frac { 1 }{ 2 }\) ∠BAD = ∠DAC …(i)
इसी प्रकार ∠BCD = 2∠BCA = 2∠DCA
∠BCA = \(\frac { 1 }{ 2 }\) ∠BCD = ∠DCA …(ii)
∆ABC तथा ∆ADC में
∠BAC = ∠DAC (समी (i) से]
∠BCA = ∠DCA (समी (ii) से]
AC = AC [उभयनिष्ठा … कोण भुजा कोण सर्वांगसमता गुणधर्म से]
∆ABC = ∆ADC
सर्वांगसम त्रिभुजों में संगत कोण व संगत(RBSESolutions.com)भुजाएँ समान होती हैं।
AB = AD तथा CB = CD
इति सिद्धम।
![]()
प्रश्न 8.
चित्र में चतुर्भुज ∆DBC के ∠ABC = ∠ABD एवं BC = BD हो, तो सिद्ध कीजिए कि ∆ABC = ∆ABD

हल
∆ABC तथा ∆ABD में,
∠ABC = ∠ABD (दिया है)
भुजा BC = भुजा BD (दिया है)
भुजा AB = भुजा AB (उभयनिष्ठ)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से
∆ABC = ∆ABD
इति सिद्धम
![]()
प्रश्न 9.
चित्र के अनुसार, AB || DC एवं AD || BC हों, तो सिद्ध कीजिए ∆ADB = ∆CBD
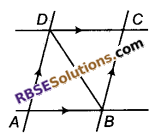
हल
दिया AB || DC तथा AD || BC
अत: ABCD समान्तर चतुर्भुज है व
AB = CD
तथा BC = AD …(i)
अब, ∆ADB तथा ∆CBD में
AB = CD तथा AD = BC [समी (i) से]
BD = BD (उभयनिष्ठ)
भुजा-भुजा-भुजा (SSS) सर्वांगसमता(RBSESolutions.com)गुणधर्म से,
∆ADB = ∆CBD
इति सिद्धम
![]()
प्रश्न 10.
चित्र में, यदि AB || DC एवं E भुजा AC का मध्य बिन्दु हो, तो सिद्ध कीजिए कि E, भुजा BD का मध्य बिन्दु होगा।

हल
∆ABE तथा ∆CDE में
∠ABD = ∠BDC (∵ AB || DC एकान्तर कोण)
इसी प्रकार ∠BAC = ∠ACD (एकान्तर कोण)
और AE = EC (∵ E, भुजा AC का मध्य बिन्दु है)
कोण-कोण भुजा (AAS) सर्वांगसम गुणधर्म से
∆ABE = ∆CDE
अतः इनकी संगत भुजाएँ बराबर होंगी।
BE = DE (सर्वांगसम(RBSESolutions.com)त्रिभुजों की संगत भुजाएँ)
इस प्रकार, E भुजा BD को मध्य बिन्दु है।
इति सिद्धम
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Ex 7.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Exercise 7.1, drop a comment below and we will get back to you at the earliest.