RBSE Solutions for Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Miscellaneous Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 7 |
| Chapter Name | त्रिभुजों की सर्वांगसमता एवं असमिकाएँ |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 41 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Miscellaneous Exercise
विविध प्रश्नमाला
वस्तुनिष्ठ प्रश्न (प्रश्न 1 से 16 तक)
प्रश्न 1.
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
(A) SAS
(B) ASA
(C) SSA
(D) SSS
उत्तर
(C) SSA
प्रश्न 2.
यदि AB = QR, BC = PR और CA = PQ है, तो
(A) ∆ABC = ∆PQR
(B) ∆CBA = ∆PR
(C) ∆BAC = ∆RPQ
(D) ∆PQR = ∆BCA
उत्तर
(B) ∆CBA = ∆PR
संकेत : प्रश्नानुसार
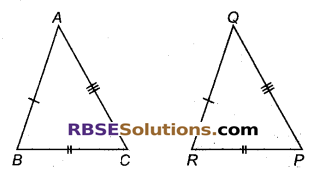
∆ABC = ∆QRP या ∆CBA = ∆PRQ
![]()
प्रश्न 3.
∆ABC में, AB = AC और ∠B = 50° है, तब ∠C बराबर है:
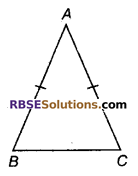
(A) 40°
(B) 50°
(C) 80°
(D) 130°
उत्तर
(B) 50°
संकेत : समान भुजाओं(RBSESolutions.com)के सम्मुख कोण समान होते हैं।
अत: ∠B = ∠C = 50°
प्रश्न 4.
∆ABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है:
(A) 80°
(B) 40°
(C) 50°
(D) 100°
उत्तर
(C) 50°
![]()
संकेत : समान भुजाओं के सम्मुख कोण समान होते हैं,
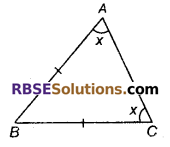
अतः ∠A = ∠C = x (माना) तो
∠x + ∠x + ∠B = 180°
⇒ ∠x + ∠x + 80° = 180°
⇒ 2∠x = 180° – 80° = 100°
⇒ ∠x = ∠A = 50°
प्रश्न 5.
∆PQR में ∠R = ∠P और QR = 4 सेमी और PR = 5 सेमी है, तब PQ की लम्बाई हैं,

(A) 4 सेमी
(B) 5 सेमी।
(C) 2 सेमी
(D) 2.5 सेमी
उत्तर
(A) 4 सेमी
संकेत : ∠P = ∠R,
QR = PQ
PQ = QR = 4 सेमी
![]()
प्रश्न 6.
D एक त्रिभुज ABC की भुजा BC पर एक बिन्दु इस(RBSESolutions.com)प्रकार स्थित है कि AD कोण BAC को समद्विभाजित करता है, तब :
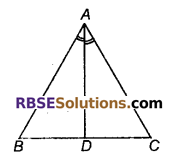
(A) BD = CD
(B) BA > BD
(C) BD > BA
(D) CD > CA
उत्तर
(B) BA > BD
संकेत : ∆ABC में, AD, ∠BAC समद्विभाजक है।
∠BAD = ∠CAD…(i)
AB = AC (ABC समद्विबाहु ∆ है।)
∠B = ∠C
∆ACD में,
∠ADB = ∠C + ∠CAD [बिहिष्कोण, सम्मुख अन्तराभिमुख कोणों के योग के बराबर होता है।]
∠ADB = ∠B + ∠BAD [समी (i) तथा (ii) को प्रयोग करने पर]
∠ADB > ∠BAD
AB > BD [किसी A में बड़े कोण की सम्मुख भुजा लम्बी होती है।
![]()
प्रश्न 7.
यह दिया है कि ∆ABC = ∆FDE है तथा AB = 5 सेमी, ∠B = 40° और ∠A = 80° है। निम्नलिखित में से कौन सत्य है?
(A) DF = 5 सेमी, ∠F = 60
(B) DF = 5 सेमी, ∠E = 60°
(C) DE = 5 सेमी, ∠E = 60°
(D) DE = 5 सेमी, ∠D = 40°
उत्तर : (B) DF = 5 सेमी, ∠E = 60°
संकेत : त्रिभुज के तीनों कोणों का योग = 180°
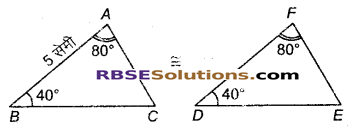
∠E + ∠D + ∠F = 180°
∠E + 40° + 80° = 180°
∠E = 180° – 120° = 60°
∆ABC = ∆FDE तथा DF = BA = 5 सेमी [सर्वांसगम त्रिभुज के संगत भुजाएँ।]
DF = 5 सेमी तथा ∠E = 60°
![]()
प्रश्न 8.
एक त्रिभुज की दो भुजाओं को लम्बाइयाँ 5 सेमी और 1.5 सेमी हैं। इस त्रिभुज की तीसरी भुजा को लम्बाई निम्नलिखित नहीं हो सकती :
(A) 3.6 सेमी
(B) 4.1 सेमी
(C) 3.8 सेमी
(D) 3.4 सेमी
उत्तर
(D) 3.4 सेमी
संकेत : त्रिभुज की किन्हीं दो भुजाओं(RBSESolutions.com)का योग तीसरी भुजा से अधिक होता है।
1.5 + 3.6 = 5.1 सेमी,
1.5 + 4.1 = 5.6 सेमी
1.5 + 3.8 = 5.3 सेमी,
1.5 + 34 = 4.9 सेमी < 5 सेमी तीसरी भुजा की लम्बाई 3.4 सेमी नहीं हो सकती। प्रश्न 9. ∆PQR में, यदि ∠R > ∠Q है, तो
(A) QR > PR
(B) PQ > PR
(C) PQ < PR
(D) QR < PR उत्तर : (B) PQ > PR
संकेत : किसी त्रिभुज में बड़े कोण की सम्मुख भुजा छोटे कोण को सम्मुख भुजा से बड़ी होती है।
अतः ∠R की सम्मुख भुजा (=PQ) > ∠Q की सम्मुख भुजा (=PR)
PQ > PR
![]()
प्रश्न 10.
त्रिभुजों ABC और PQR में, AB = AC, ∠C = ∠P और ∠B = ∠Q है। ये दोनों त्रिभुज है।
(A) समद्विबाहु परंतु सर्वांगसम नहीं
(B) समद्विबाहु और सर्वांगसम
(C) सर्वांगसम(RBSESolutions.com)परन्तु समद्विबाहु नहीं
(D) न तो सर्वांगसम और न ही समद्विबाहु
उत्तर
(A) समद्विबाहु परंतु सर्वांगसम नहीं
संकेत :
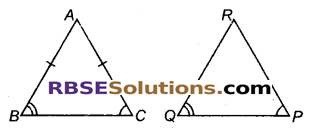
चूंकि AB = AC, इसलिए ये त्रिभुज समद्विबाहु हैं। ये सर्वांगसम नहीं हैं क्योंकि RQ = RP परन्तु यह आवश्यक नहीं है कि ये AB के बराबर हों।
प्रश्न 11.
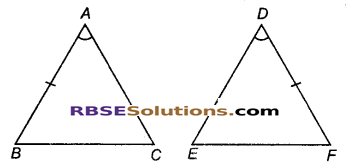
त्रिभुजों ABC और DEF में, AB = FD तथा ∠A = ∠D है। दोनों त्रिभुज SAS अभिगृहीत के अन्तर्गत सर्वांगसम होगे, यदि :
(A) BC = EF
(B) AC = DE
(C) AC = EF
(D) BC = DE
उत्तर : (B) AC = DE
संकेत : अत: SAS अभिगृहीत के अन्तर्गत सर्वांगसम होने के लिए AC = DE होना चाहिए।
![]()
प्रश्न 12.
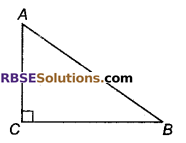
समकोण त्रिभुज ABC में कोण C समकोण हो तो, सबसे बड़ी भुजा होगी:
(A) AB
(B) BC
(C) CA
(D) कोई नहीं
उत्तर
(A) AB
संकेत : सबसे बड़े कोण के सामने वाली(RBSESolutions.com)भुजी सबसे बड़ी होती है। चित्र में ∠C (=90°) सबसे बड़ा कोण है।
इसलिए AB सबसे बड़ी भुजा होगी।
![]()
प्रश्न 13.
किसी त्रिभुज की दो भुजाओं को अन्तर तीसरी भुजा से होता है:
(A) अधिक
(B) समान
(C) कम
(D) आधा
उत्तर
(C) कम
प्रश्न 14.
यदि किसी त्रिभुज की दो भुजाएँ असमान हो, तो बड़ी भुजा के सामने का कोण होता है:
(A) बड़ा
(B) छोटा
(C) बराबर
(D) आधा
उत्तर
(A) बड़ा
प्रश्न 15.
त्रिभुज का परिमाप उसकी मध्यिकाओं के योग से होता है-
(A) अधिक
(B) कम
(C) समान
(D) आधा
उत्तर
(A) अधिक
![]()
प्रश्न 16.
त्रिभुज के तीनों शीर्ष लम्बों का योग उसके परिमाप से होता है:
(A) अधिक
(B) समान
(C) आधा
(D) कम
उत्तर
(D) कम
प्रश्न 17.
यदि ΔABC में AB = AC हो तथा ∠A < 60° हो, तो भुजा BC एवं AC में सम्बन्ध लिखिए।
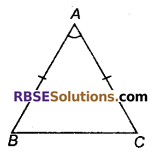
हल
ΔABC में,
AB = AC तथा ∠A < 60°
∠B = ∠C (समान भुजाओं के सम्मुख कोण) हम जानते हैं कि ΔABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠A < 60° और ∠B = ∠C ⇒ ∠B = ∠C > 60°
और ∠A < 60° (दिया है) अब ∠B = ∠C > ∠A
∠B > ∠A (सम्मुख भुजाओं के कोण)
⇒ AC > BC
⇒ BC < AC
![]()
प्रश्न 18.
चित्र में, भुजा AB एवं AC में सम्बन्ध लिखिए।
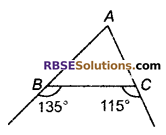
हल
ΔABC में,
∠CBA = 180° – 135° = 45°
तथा ∠BCA = 180° – 115° = 65°
∠BCA > ∠CBA
AB > AC (सम्मुख कोणों की भुजाएँ)
प्रश्न 19.
किसी त्रिभुज ABC में, ∠A > ∠B एवं ∠B > ∠C हो, तो सबसे छोटी भुजा कौन-सी होगी?
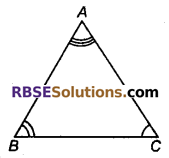
हल:
∠A > ∠B
तथा ∠B > ∠C
∠A > ∠B > ∠C
सबसे छोटा(RBSESolutions.com)कोण C है।
अत: सबसे छोटी भुजा = ∠C के सामने वाली
भुजा = AB
![]()
प्रश्न 20.
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
हल
समबाहु त्रिभुज में तीनों कोण समान होते हैं।
माना प्रत्येक कोण x है। तब तीनों कोणों का योग = 180°
x + x + x = 180°
3x = 180°
x = 60° अतः एक समबाहु त्रिभुज का प्रत्येक कोण 60° का। होता है।
प्रश्न 21.
P कोण ABC के समद्विभाजक पर स्थित कोई बिन्दु है। यदि P से होकर BA के समान्तर खींची गई रेखा BC से Q पर मिलती है, तो सिद्ध कीजिए कि BPQ एक समद्विबाहु त्रिभुजे है।
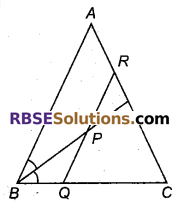
हल
ΔABC में,
RQ || AB
∠PBA = ∠PBQ …(i)
RQ || AB
∠PBA = ∠BPQ (एकान्तरं कोण) …(ii)
समी (i) तथा (ii) से
∠PBQ = ∠BPQ [समी (i) से]
बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
BQ = QP
अत: ABPQ एक समद्विबाहु त्रिभुज है।
इति सिद्धम्
![]()
प्रश्न 22.
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
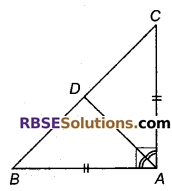
हल
ΔABC में, ∠A समकोण है।
AD, ∠A का समद्विभाजक है।
ΔABD तथा ΔACD में,
∠DAB = ∠DAC = 45° …(i)
AB = AC (दिया है) …(i)
∠C = ∠B
अतः ΔABD = ΔACD
तब ∠DAB = ∠DBA = 45°
इसी प्रकार ∠DAC = ∠DCA = 45°
अतः AD = CD …(iv)
इसी प्रकार AD = BD अतः BD = CD
बायाँ पक्ष
BC = BD + DC
= BD + BD (समीकरण (iv) से)
= 2BD
= 2AD
= दायाँ पक्ष
इति सिद्धम्
![]()
प्रश्न 23.
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिन्दु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखण्ड BC का लम्ब(RBSESolutions.com)समद्विभाजक है।
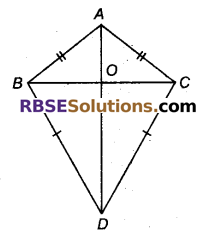
हल
यहाँ AB = AC तथा DB = DC दिया हुआ है। हमें दर्शाना है कि AD ⊥ BC है और AD रेखाखण्ड BC को समद्विभाजित करती है। माना, रेखा AD रेखाखण्ड BC को O पर प्रतिच्छेद करती है। ΔABD तथा ΔACD में, AB = AC (दिया है)
BD = CD (दिया है)
AD = AD (उभयनिष्ठ भुजा)
भुजा–भुजा-भुजा गुणधर्म से,
ΔABD = ΔACD
इसलिए, ∠BAD = ∠CAD
सर्वांगसम त्रिभुजों के संगत भाग
अब ΔAOB व ΔAOC में,
AB = AC (दिया है)
∠BAO = ∠OAC (∠BAD = ∠CAD)
तथा AO = AO (उभयनिष्ठ)
भुजा कोण भुजा(RBSESolutions.com)गुणधर्म से, ΔAOB = ΔAOC
सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।
और ∠BOA = ∠COA एवं BO = CO …… (i)
साथ ही, ∠BOA + ∠COA = 180° (रैखिक कोण युग्म)
इसलिए, 2∠BOA = 180°
⇒ ∠ BOA = 90°…(ii)
समीकरण (i) व (ii) से स्पष्ट है कि रेखा AD रेखाखण्डे BC का लम्ब समद्विभाजक है।
इति सिद्धम्
![]()
प्रश्न 24.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमशः BC और AC पर शीर्ष लम्ब है। सिद्ध कीजिए कि AE = BD है।
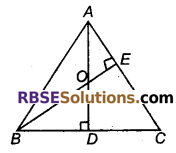
हल
दिया है: AC = BC ⇒ ∠B = ∠A …(i) (समान भुजाओं के सम्मुख कोण)
ΔADB तथा ΔBEA में
AB = AB (उभयनिष्ठ भुजा)
∠B = ∠A (समी (i) से)
∠ADB = ∠BEA (प्रत्येक 90° है)
कोण-कोण-भुजा(RBSESolutions.com)गुणधर्म से, ΔADB = ΔBEA
BD = AE (सर्वांगसम त्रिभुजों की संगत भुजाएँ)
इति सिद्धम्
![]()
प्रश्न 25.
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता है।
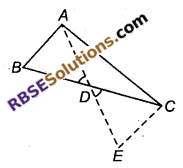
हल
दिया है : त्रिभुज ABC की माध्यिका AD है।
सिद्ध करना है : AB + AC > 2AD
रचना : चित्रानुसार AD को E तक इस प्रकार आगे बढ़ाया कि DE = AD हो एवं C तथा E को मिलाया।
उपपत्ति: ΔADB एवं ΔEDC में,
AD = DE (रचना से)
BD = DC (दिया है)
∠ADB = ∠EDC (शीर्षाभिमुख कोण)
भुजा-कोण-भुजा (RBSESolutions.com)गुणधर्म से,
ΔADB = ΔEDC
AB = CE
अब ΔACE में,
AC + CE > AE
AC + AB > AE [∵ CE = AB]
AC + AB > 2AD [∵ AE = 2AD]
इति सिद्धम।
![]()
प्रश्न 26.
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिन्दु है तथा BD = \(\frac { 1 }{ 2 }\) AC है। दर्शाइए कि ∠ABC एक समकोण है।
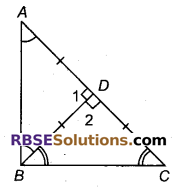
हल
दिया है : BD = \(\frac { 1 }{ 2 }\) AC तथा D, AC का मध्य बिन्दु है।
अर्थात AD = CD
AD = CD = BD
AD = BD
∠BAD = ∠ABD (समान भुजाओं के सम्मुख कोण समान होते हैं)
माना ∠BAD = ∠ABD = ∠x
ΔABD में,
∠ABD + ∠BAD + ∠1 = 180°
∠x + ∠x + ∠1 = 180
∠1 = 180 – 2∠x …(i)
इसी प्रकार ΔBCD में,
BD = CD
∠CBD = ∠BCD
माना ∠BCD = ∠CBD = ∠y
⇒ ∠BCD + ∠CBD + ∠2 = 180°
⇒ ∠y + ∠y + ∠2 = 180°
⇒ ∠2 = 180° – 2∠y …(ii)
समी (i) तथा (ii) को जोड़ने पर
∠1 + ∠2 = 180° – 2∠x + 180° – 2∠y
⇒ 180° = 360° – 2(∠x + ∠y) (रैखिक कोण युग्म से, ∠1 + ∠2 = 180°]
⇒ 2(∠x + ∠y) = 360° – 180° = 180°
⇒ ∠x + ∠y = 90°, ∠A + ∠C = 90° …(iii)
ΔABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠B + 90° = 180°
⇒ ∠B = 90° [समी (iii) का प्रयोग करने पर]
⇒ ∠ABC = एक समकोण,
इति सिद्धम
![]()
प्रश्न 27.
एक समकोण त्रिभुज में सिद्ध कीजिए कि कर्ण के मध्य-बिन्दु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखण्ड कर्ण का आधा होता है।
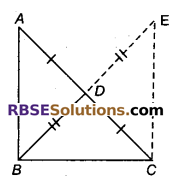
हल
दिया है : माना, त्रिभुज ABC मे, ∠B = 90° तथा कर्ण AC का मध्य बिन्दु D है।
सिद्ध करना है : BD = \(\frac { 1 }{ 2 }\) AC
रचना : BD को E तक
इस प्रकार(RBSESolutions.com)बढ़ाते हैं कि BD = DE तथा CE को मिलाया।
उपपत्ति :
ΔABD तथा ΔCED में
AD = DC
BD = DE (रचना से)
∠ADB = ∠CDE (शीर्षाभिमुख कोण)
भुजा कोण भुजा सर्वांगसमता गुणधर्म से।
ΔABD = ΔCED
AB = CE
तथा ∠ABD = ∠CED
∠ABE = ∠CBE
(∵ सर्वांगसम त्रिभुजों के संगत भाग समान होते हैं। अतः रेखाओं AB तथा CE को एक त्रिर्यक रेखा इस प्रकार काटती है कि एकान्तर कोण ∠ABE तथा ∠CEB समान हैं)
अत: AB || CE
∠ABC + ∠ECB = 180°
[तिर्यक रेखा के एक ही ओर बने अन्तः कोणों का योग 180° होता है।
90° + ∠ECB = 180°
∠ECB = 180° – 90° = 90°
अब ΔABC तथा ΔECB में,
AB = EC (समी (i) से)
BC = BC (उभयनिष्ठ भुजा]
तथा ∠ABC = ∠ECB [प्रत्यक 90° है।
भुजा कोण भुजा गुणधर्म से, ΔABC = ΔECB
AC = BE
\(\frac { 1 }{ 2 }\) AC = \(\frac { 1 }{ 2 }\) BE = BD
इति सिद्धम्।
![]()
प्रश्न 28.
चित्र में, यदि AB = AC हो, तो भुजा AB एवं AD में संबंध लिखिए।
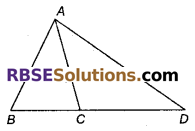
हल
AB = AC (दिया है)
∠B = ∠ACB …(i)
ΔACD में, (बहिष्कोण, अपने सम्मुख दो कोणों के योग के बराबर होता है।)
∠B = ∠CAD + ∠D [समी (i) का प्रयोग करने पर)]
⇒ ∠B > ∠D
⇒ AD > AB [किसी त्रिभुज में कोण की सम्मुख भुजा लम्बी होती है।]
प्रश्न 29.
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
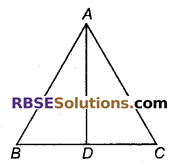
हल
हाँ, यह सत्य है।
कारण : हम जानते हैं कि त्रिभुज में दो भुजाओं का योग त्रिभुज की तीसरी भुजा से अधिक होता है।
ΔABD में,
AB + BD > AD …(i)
तथा ΔACD में,
AC + CD > AD …(ii)
समीकरण (i) व (ii) को जोड़ने पर
AB + BD + AC + CD > 2AD
⇒ AB + (BD + DC) + CA > 2AD
अतः AB + BC + CA > 2AD
![]()
प्रश्न 30.
M किसी त्रिभुज ABC की भुजा BC पर स्थिति एक बिन्दु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
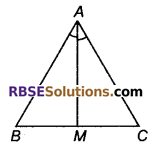
हल
हाँ यह सत्य है।
कारण : हम जानते हैं कि त्रिभुज में किन्हीं दो भुजाओं । का योग तीसरी भुजा से अधिक होता है।
ΔABM तथा ΔACM में,
AB+ BM > AM …(i)
AC + CM > AM …(ii)
समीकरण (i) व (ii) को जोड़ने पर
AB + BM + AC + CM > 2AM
⇒ AB + (BM + MC) + CA > 2AM
⇒ AB + BC + CA > 2AM
अतः परिमाप > 2AM
![]()
प्रश्न 31.
एक ΔPSR की भुजा SR पर एक बिन्दु Q इस प्रकार स्थित है कि PQ = PR है। सिद्ध कीजिए कि PS > PQ है।
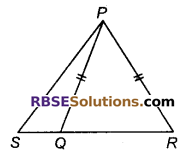
हल
ΔPQR में, PQ = PR
ΔPSQ में,
∠PQR = ∠SPQ + ∠S [∵ बहिष्कोण, अपने सम्मुख दो अन्त कोणों के योग के बराबर होता है।]
⇒ ∠PRQ = ∠SPQ + ∠S (∵ ∠PQR = ∠PRQ)
⇒ ∠PRQ > ∠S
PS > PR [∵ किसी त्रिभुज में बड़े कोण की सम्मुख भुजा लम्बी होती है।
इति सिद्धम्।
प्रश्न 32.
ΔPQR की भुजा QR पर S कोई बिन्दु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
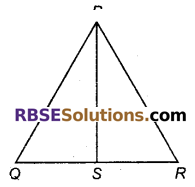
हल
दिया है: ΔPQR में, QR पर बिन्दु S है।
हम जानते हैं कि किसी भी त्रिभुज में दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
ΔPQS में,
PQ + QS > PS …(i)
तथा ΔPSR में,
PR + RS > PS ….(ii)
समीकरण (i) व (ii) को जोड़ने पर
(PQ + QS) + (PR + RS) > 2PS
⇒ PQ + (QS + SR) + RP > 2PS
⇒ PQ + QR + RP > 2PS
इति सिद्धम्।
![]()
प्रश्न 33.
AB = AC वाले एक त्रिभुज ABC की भुजा AC पर D कोई बिन्दु स्थित है। दर्शाइए कि CD < BD है।
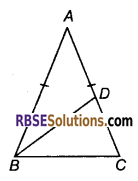
हल
ΔABC, जिसमें AB = AC व AC पर बिन्दु D है।
सिद्ध करना है : CD < BD उपपत्ति : AB = BC ∠ABC = ∠ACB ΔBCD में, ∠DCB > ∠CBD
बड़ी भुजा के सामने का कोण बड़ा तथा छोटी भुजा के सामने का कोण छोटा होता है।
भुजा BD > भुजा CD
अत: CD ∠A एवं ∠D > ∠E हो, तो सिद्ध कीजिए की AE > BD.
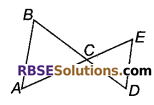
हल
∠B > ∠A तथा
∠D > ∠E (दिया है)।
AC > BC …(i)
तथा CE > CD …(ii)
समीकरण (i) व (ii) को जोड़ने पर,
AC + CE > BC + CD
AE > BD
इति सिद्धम्।
![]()
प्रश्न 35.
किसी त्रिभुज ABC में, AB > AC एवं भुजा BC पर कोई बिन्दु D हो, तो सिद्ध कीजिए AB > AD
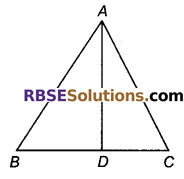
हल
दिया है, ΔABC में,
AB > AC …(i)
∠C > ∠B [किसी त्रिभुज में बड़ी भुजा का सम्मुख कोण बड़ा होता है।]
∠ADB = ∠CAD + ∠C
⇒ ∠ADB > ∠C …(ii)
समी. (i) द (ii) से, ∠ADB > ∠B [किसी त्रिभुज में बड़े कोण की सम्मुख भुजो लम्बी होती है।]
इति सिद्धम्।
प्रश्न 36.
सिद्ध कीजिए कि त्रिभुज की तीनों भुजाओं का योग उसकी तीनों माध्यिकाओं के योग से अधिक होता है।
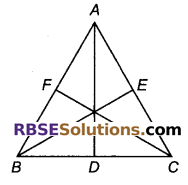
हल
दिया है : ΔABC में,
AD, BE और CF इसकी माध्यिकाएँ हैं।
सिद्ध करना है : AB + BC + AC > AD + BE + CE
उपपत्ति: हम जानते हैं B , कि किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा पर खींची गई माध्यिका के दुगुने से अधिक होता है।
चित्र में शीर्ष A से खींची गई(RBSESolutions.com)भुजा BC पर AD माध्यिका है।
AB + AC > 2AD …(i)
B शीर्ष से खींची गई भुजा CA पर BE माध्यिका है।
BC + AB > 2BE ……(ii)
C शीर्ष से खींची गई भुजा AB पर CF माध्यिका है।
AC + BC > 2CF …(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर,
(AB + AC) + (BC + AB) + (AC + BC) > 2AD + 2BE + 2CF
⇒ 2 (AB + BC + AC) > 2 (AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF
इति सिद्धम्।
![]()
प्रश्न 37.
चित्र में त्रिभुज में कोई अन्त: बिन्दु O हो तो सिद्ध कीजिए कि (BC + AB + AC) < 2(OA + OB + OC) हैं
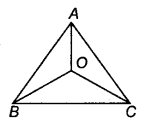
हल
दिया है : ΔABC में, O एक अन्तः बिन्दु है।
सिद्ध करना है :
(BC + AB + AC) < 2 (OA + OB + OC) उपपत्ति: ΔAOB में, AO + BO > AB…(i)
(किसी त्रिभुज में दो भुजाओं का योग तीसरी भुजा से अधिक होता है)।
इसी(RBSESolutions.com)प्रकार ΔBOC में, OB + OC > BC …(ii)
इसी प्रकार ΔAOC में, OC + OA > AC…(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर,
(AO + BO) + (OB + OC) + (OC + OA) > AB + BC + AC
⇒ 2 (OA + OB + OC) > AB + BC + AC
⇒ AB + BC + AC < 2 (OA + OB + OC)
इति सिद्धम्।
![]()
प्रश्न 38.
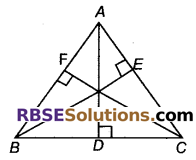
सिद्ध कीजिए कि त्रिभुज के तीनों शीर्ष लम्बों का योग त्रिभुज के परिमाप से कम होता है।
हल
दिया है : ΔABC में,
A, B तथा C से BC, AC व AB पर डाले गये लम्ब AD, BE तथा CF हैं।
सिद्ध करना है : AD + BE + CF < AB + BC + CA
उत्पत्ति : हम जानते हैं कि किसी सरल रेखा या रेखाखण्ड बाह्य बिन्दु से खींचे गए सभी रेखाखण्डों में लम्ब सबसे छोटा होता है।
ΔABD में, ∠ADB =90°
AD < AB …(i)
ΔBEC में,
BE ⊥ AC
BE < BC …(ii)
इसी प्रकार, ΔACF में, CF ⊥ AB
CF < AC …(iii)
(i), (ii) और (iii) को जोड़ने पर,
AD + BE + CF < AB + BC + AC
इति सिद्धम्।
![]()
प्रश्न 39.
सिद्ध कीजिए कि किसी त्रिभुज की दो भुजाओं का अन्तर तीसरी भुजा से छोटा होता है।
हल
दिया है : ΔABC
सिद्ध करना है
(i) AC – AB < BC,
(ii) BC – AC < AB,
(iii) BC – AB < AC रचना : भुजा AC पर ऐसा बिन्दु D लिया जिसमें AD = AB, B और D को मिलाया। उपपत्ति: ΔABD में, ∠3 > ∠1 ……(i)
(किसी त्रिभुज को बहिष्कोण किसी भी अन्त:कोण से बड़ा होता है।)
ΔBCD में, ∠2 > ∠4 ……(ii)
(∵ बहिष्कोण, किसी भी अन्त:कोण से बड़ा होता है।)
ΔABD में, AB = AD
∠2 = ∠1 …(iii)
(∵ समान भुजाओं के सम्मुख कोण समान होते हैं।)
समीकरण (i) और (iii) से, ∠3 > ∠2 …(iv)
समीकरण (ii) और (iv) से, ∠3 > ∠2
और ∠2 > ∠4
∠3 > ∠4
BC > CD (∵ किसी त्रिभुज में बड़े कोण के सम्मुख भुजा लम्बी होती है)।
CD < BC
⇒ AC – AD < BC [CD = AC – AD]
⇒ AC – AB < BC [AD = AB]
इसी प्रकार, हम सिद्ध कर सकते हैं कि
BC – AC < AB
और BC – AB < AC.
इति सिद्धम्।
![]()
प्रश्न 40.
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर है।
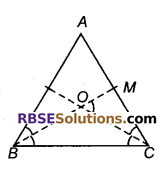
हल
दिया है, ΔABC में,
AB = AC तो AB व AC के द्वारा BC पर बनाया गया कोण ∠B व ∠C समान होंगे।
∠B = ∠C …(i)
OB तथा OC कोण B व C के क्रमशः समद्विभाजक हैं।
∠ABO = ∠OBC तथा ∠ACO = ∠OCB
∠OBA = ∠OBC = ∠ACO = ∠OCB = x (माना)
त्रिभुजों के तीनों अन्त: कोणों का योग 180° होता है।
∠BỌC + ∠OCB + ∠CBO = 180°
∠BOC + x + x = 180°
∠BOC = 180° – 2x …(ii)
∠MOB = 180°(सरल रेखा कोण)
या ∠MOC + ∠BOC = 180°
∠MOC = 180° – ∠BOC …(iii)
समीकरण (ii) से ∠BOC का मान समी (iii) मे रखने पर,
∠MOC = 180° – (180° – 2x)
= 180° – 180° + 2x
= 2x
∠BOC = x + x = ∠OBC + ∠OCB = ∠OBA + ∠OBC = ∠ABC
अतः ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर है।
इति सिद्धम्।
![]()
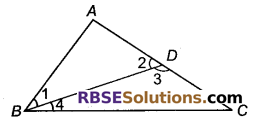
प्रश्न 41.
चित्र में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।
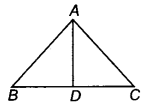
हल
AD, ∠BAC का समद्विभाजक हैं ।
∵ ∠1 = ∠2
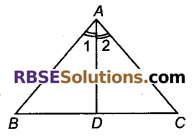
ΔADC में,
∠ADB = ∠2 + ∠C
∠ADB > ∠2
∠ADB > ∠1 [∵ ∠1 =∠2]
AB > BD [∵ बड़े कोण की सम्मुख भुजा लम्बी होती है।]
इति सिद्धम्।
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Miscellaneous Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 7 त्रिभुजों की सर्वांगसमता एवं असमिकाएँ Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.