RBSE Solutions for Class 9 Maths Chapter 7 Congruence and Inequalities of Triangles Miscellaneous Exercise

RBSE Solutions for Class 9 Maths Chapter 7 Congruence and Inequalities of Triangles Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 7 Congruence and Inequalities of Triangles Miscellaneous Exercise.

Board	RBSE
Class	Class 9
Subject	Maths
Chapter	Chapter 7
Chapter Name	Congruence and Inequalities of Triangles
Exercise	Miscellaneous Exercise
Number of Questions Solved	40
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 7 Congruence and Inequalities of Triangles Miscellaneous Exercise

Multiple Choice Questions (Q1 to Q16)

Question 1.
Which of the following is not a criterion (RBSESolutions.com) for congruence of triangle?
(A) SAS
(B) ASA
(C) SSA
(D) SSS
Solution.
(C) SSA

Question 2.
If AB = QR; BC = PR and CA = PQ, then:
(A) ΔABC = ΔPQR
(B) ΔCBA = ΔPRQ
(C) ΔBAC = ΔRPQ
(D) ΔPQR = ΔBCA
Solution.
(B) ΔCBA = ΔPRQ

Question 3.
In ΔABC, AB = AC and ∠B = 50°, then ∠C is equal to:
(A) 40°
(B) 50°
(C) 80°
(D) 130°
Solution.
(B) 50°

Question 4.
In ΔABC, BC = AB and ∠B = 80°, then ∠A is equal to:
(A) 80°
(B) 40°
(C) 50°
(D) 100°
Solution.
(C) 50°

Question 5.
In ΔPQR. ∠R = ∠P and QR = 4 cm and PR = 5 cm, then length of PQ is:
(A) 4 cm
(B) 5 cm
(C) 2 cm
(D) 2.5 cm
Solution.
(A) 4 cm

Question 6.
In ΔABC, D is a point on the side BC is situated in (RBSESolutions.com) such a way that AD is the bisector of ∠BAC then
(A) BD = CD
(B) BA > BD
(C) BD > BA
(D) CD > CA
Solution.
(A) BD = CD

Question 7.
Given that ΔABC = ΔFDE and AB = 5 cm, ∠B = 40° and ∠A = 80° then which of the following relation is true?
(A) DF = 5 cm, ∠F = 60°
(B) DF = 5 cm, ∠E = 60°
(C) DE = 5 cm, ∠E = 60°
(D) DE = 5 cm, ∠D = 40°
Solution.
(B) DF = 5 cm, ∠E = 60°

Question 8.
The length of the two sides of (RBSESolutions.com) a triangle are 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
(A) 3.6 cm
(B) 4.1 cm
(C) 3.8 cm
(D) 3.4 cm
Solution.
(D) 3.4 cm

Question 9.
In ΔPQR, if ∠R > ∠Q, then
(A) QR > PR
(B) PQ > PR
(C) PQ < PR
(D) QR < PR Solution. (B) PQ > PR

Question 10.
In Δ’s ABC and PQR, AB = AC, ∠C = ∠P, and ∠B = ∠Q then these (RBSESolutions.com) two triangles are:
(A) Isosceles but not congruent
(B) Isosceles and congruence
(C) Congruent but not isosceles
(D) Neither isosceles nor congruent
Solution.
(A) Isosceles but not congruent

Question 11.
In Δ’s ABC and DEF, AB = FD and ∠A = ∠D, the two triangles will be congruent by SAS congruence rule if:
(A) BC = EF
(B) AC = DE
(C) AC = EF
(D) BC = DF
Solution.
(B) AC = DE

Question 12.
If ∠C is right angle in ΔABC, then the (RBSESolutions.com) largest side is:
(A) AB
(B) BC
(C) CA
(D) None
Solution.
(A) AB

Question 13.
The difference of any two sides of a triangle is ………. than the third side:
(A) greater
(B) equal
(C) less
(D) half
Solution.
(C) less

Question 14.
If two sides of a triangle are unequal (RBSESolutions.com) then opposite angle of larger side is:
(A) greater
(B) less
(C) equal
(D) half
Solution.
(A) greater

Question 15.
The perimeter of the triangle is ………. than the sum of its three medians.
(A) greater
(B) less
(C) equal
(D) half
Solution.
(A) greater

Question 16.
The sum of altitudes of a triangle is ………. than the perimeter of the triangle.
(A) greater
(B) equal
(C) half
(D) less
Solution.
(D) less

Question 17.
In an ∆ABC, if AB = AC and ∠A < 60° then write (RBSESolutions.com) the relation between BC and AC.
Solution.
BC < AC.

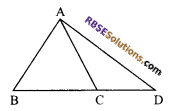
Question 18.
In figure, what is the relation between AB and AC?

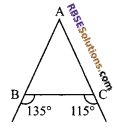
Solution.
∠ABC = 180° – 135° = 45°,
∠ACB = 65°
i.e. ∠ACB > ∠ABC,
⇒ AB > AC.

Question 19.
In ∆ABC, ∠A > ∠B and ∠B > ∠C, then write (RBSESolutions.com) the smallest side.
Solution.
According to given relation ∠A > ∠C.
Side AB will be least because ∠C is least.

Question 20.
Find each angle of an equilateral triangle.
Solution.
All sides are equal to each angle will be equal to 60°.

Question 21.
P is a point on the bisectors of ∠ABC. If the line (RBSESolutions.com) through P, parallel to BA, meet BC at Q. Prove that BPQ is an isosceles triangle.
Solution.
P lie on the bisector of ∠ABC.
QT || BA
(∠1 + ∠2) = ∠3 (corresponding angles)

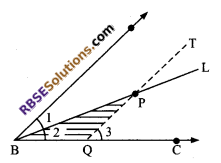
But BL is the bisector of ∠ABC
∠1 = ∠2
Also ∠3 = ∠2 + ∠BPQ
∠1 + ∠2 = ∠2 + ∠BPQ
⇒ ∠1 = ∠BPQ
⇒ ∠2 = ∠BPQ [∵ ∠1 = ∠2]
⇒ QP = BQ
∆BPQ is an isosceles triangle.

Question 22.
ABC is a right (RBSESolutions.com) triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2 AD.
Solution.
In ∆ABD and ∆ACD
AB = AC (given)
∠BAD = ∠CAD

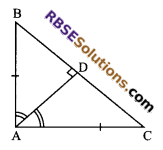
As AD is bisector of ∠A and AD = AD
⇒ ∆DAB = ∆DAC (by SAS congruency rule)
⇒ ∠ADB = ∠ADC (by c.p.c.t)
⇒ ∠ADB = ∠ADC = 90°
and BD = DC
In ∆ABD,
AD² + BD² = AB² …(i)
⇒ AD² + DC² = AC² …(ii)
Adding (i) and (ii), we get
2 AD² + BD² + DC² = AB² + AC²
⇒ 2AD² + BD² + DC² = BC²
⇒ 2 AD² + 2BD² = BC²
⇒ 2 (AD² + BD²) = BC²

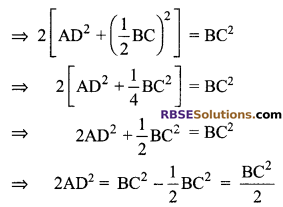
⇒ 4 AD² = BC²
⇒ 2 AD = BC
i.e. BC = 2AD
Hence proved.

Question 23.
∆ABC and ∆DBC are two triangles (RBSESolutions.com) on the same base BC such that A and D lie on the opposite side of BC. AB = AC and BD = DC. Show that AD is the ⊥ bisector of BC.
Solution.
In ∆BAD and ∆CAD
AB = AC (given)
BD = DC (given)
and AD = AD (common)
∆BAD = ∆CAD (by SSS congruence rule)

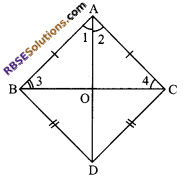
∠1 = ∠2 (by c.p.c.t)
Also AB = AC (given)
∠3 = ∠4 (angle opposite to equal sides are equal)
∆BAO = ∆CAO
⇒ BO = OC (by c.p.c.t)
or AO bisects BC (by c.p.c.t)
Also ∠AOB = ∠AOC (by c.p.c.t)
But ∠AOB + ∠AOC = 180°
⇒ ∠AOB = ∠AOC = 90°
⇒ AD is perpendicular bisector of BC.

Question 24.
ABC is an isosceles (RBSESolutions.com) triangle in which AC = BC and AD and BE are altitude on the sides BC and AC respectively. Prove that AE = BD.
Solution.
In ∆ABC,
AC = BC (given)
∠EAB = ∠DBA …(i) (angles opposite to equal sides are equal)

Now in ∆EAB and ∆DAB
∠AEB = ∠ADB = 90° (given)
∠EAB = ∠DBA [using (i)]
and AB = AB (common)
∆DAB = ∆EAB (by AAS congruencey rule)
⇒ AE = BD (by c.p.c.t)

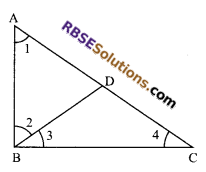
Question 25.
Prove that the sum of any two sides (RBSESolutions.com) of a triangle is greater than twice the median drawn to the third side?
Solution.
Given: In ∆ABC, AD is the median
To prove: AB + AC > 2AD
Construction: Produce AD up to E, such that AD + DE and Join EC.

Proof: In ∆ADB and ∆EDC
AD = DE (by construction)
BD = DC (given)
and ∠ADB = ∠EDC (vertically opposite angles)
∆ADB = ∆EDC (by SAS congruency property)
⇒ AB = CE (by c.p.c.t)
Now in ∆ACE
AC + CE > AE
⇒ AC + AB > AE (∵ AB = CE) (Proved above)
⇒ AC + AB > 2AD (∵ AE = 2AD)
Hence proved.

Question 26.
In ∆ABC, D is the mid-point (RBSESolutions.com) of side AC such that BD = \(\frac { 1 }{ 2 }\) AC. Show that ∠ABC = 90°.
Solution.
D is mid-point of AC
⇒ AD = DC = \(\frac { 1 }{ 2 }\) AC

But BD = \(\frac { 1 }{ 2 }\) AC (given)
⇒ AD = DC = BD
In ∆ABD
AD = BD
⇒ ∠2 = ∠1 = x (angles opposite to equal sides are equal)
Also BD = DC
∠3 = ∠4 = x
In ∆ABC
∠1 + (∠2 + ∠3) + ∠4 = 180°
⇒ x + (x + x) + x = 180°
⇒ 4x = 1 80°
⇒ x = 45°
⇒ ∠ABC = x + x = 45° + 45° = 90°
Hence proved.

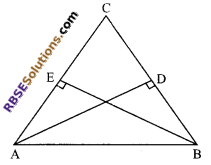
Question 27.
Prove that the line segment joining (RBSESolutions.com) the mid-point of the hypotenuse of a right triangle to the vertex of the right angle is equal to half the hypotenuse.
Solution.
Let ABC is a right triangle right angled at B.
Let P be the mid-point of the hypotenuse AC.
Through P, draw PQ || BC

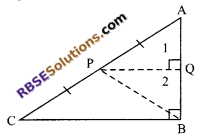
PQ || BC
⇒ ∠1 = ∠B (corresponding angle)
⇒ ∠2 = ∠1 = 90°
In ∆ABC, P is the (RBSESolutions.com) mid-point of AC and PQ || BC
Q must be mid-point of AB (converse of mid-point theorem)
⇒ AQ = QB …(i)
Now in ∆AQP and ∆BPQ
AQ = QB
∠2 = ∠1 = 90°
PQ = PQ
∆AQP = ∆BPQ (by SAS congruency rule)
⇒ AP = PB (by c.p.c.t)
Thus, AP = PB = PC
Hence in other words, we can say that the point P is equi-distance from (RBSESolutions.com) the vertices of a right angled triangle ABC.

Question 28.
In figure, if AB = AC, what is the relation between AB and AD.

Solution.
AD > AB

Question 29.
AD is the median of any ∆ABC. Is it true to say that AB + BC + CA > 2AD. Give reason for your answer.
Solution.
Yes, if AD is median of ∆ABC

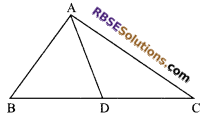
⇒ AB + BD > AD …(i) (sum of any two sides of a A is greater than third side)
and AC + DC > AD …(iii) (reason as above)
⇒ AB + (BD + DC) + AC > 2 AD
⇒ AB + BC + CA > 2AD

Question 30.
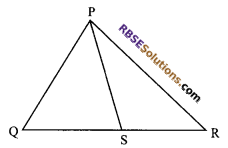
M is any point on the side BC of ∆ABC in such (RBSESolutions.com) a way that AM is the bisector of ∠BAC. Is it true to say that perimeter of ∆ABC is greater than 2 AM? Give reason for your answer.
Solution.
Yes, AB + BM > AM …(i)
also AC + CM > AM …(ii)

Adding (i) and (ii), we get
AB + (BM + CM) + AC > 2AM
⇒ AB + BC + CA > 2AM
⇒ Perimeter of ∆ABC > 2AM

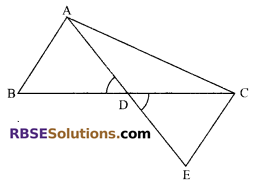
Question 31.
In figure, Q is a point on side SR of ∆PSR such that PQ = PR. Prove that PS > PQ.

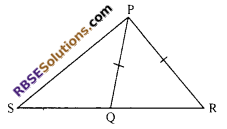
Solution.
In ∆PQR
PQ = PR
∠PQR = ∠PRQ …(i) (angles opposite to (RBSESolutions.com) equal sides of a triangle are equal)
In ∆PSQ
Ext. ∠PQR > ∠PSQ …(ii)
From (i) and (ii), we get
∠PRQ > ∠PSQ
⇒ PS > PR (side opposite to greater angle is longer)
⇒ PS > PQ (∵ PQ = PR)

Question 32.
In ∆PQR, S is any point on side QR. Show that PQ + QR + RP > 2PS.
Solution.
In ∆PQR,
PQ + QS > PS …(i) (∵ the sum of any two sides of a triangle is greater than the third side)

In ∆PRS,
PR + RS > PS (∵ The sum of (RBSESolutions.com) any two sides of a triangle is greater than the third side)
On adding (i) and (ii), we get
(PQ + QS) + (PR + RS) > 2PS
⇒ PQ + (QS + RS) + PR > 2PS
⇒ PQ + QR + PR > 2PS
⇒ PQ + QR + RP > 2PS
Hence proved.

Question 33.
In an ∆ABC with AB = AC, D is any point on the side AC. Show that CD < BD.
Solution.
In ∆ABC

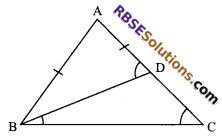
AB = AC (given)
⇒∠B = ∠C
⇒ ∠ADB = ∠DBC + ∠C (exterior angle (RBSESolutions.com) is equal to sum of opposite interior angles)
⇒ ∠ADB > ∠C
⇒ AB > BD
But AB = AC
⇒ AD + DC > BD
⇒ BD > CD
Hence proved.

Question 34.
In figure, ∠B > ∠A and ∠D > ∠E then show that AE > BD.

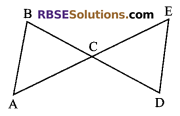
Solution.
∠B > ∠A
⇒ AC > BC …(i)
Also ∠D > ∠E
CE > CD …(ii) (greater angle has larger side opposite to it)
Adding (i) and (ii), we get AC + CE > BC + CD
⇒ AE > BD
Hence proved.

Question 35.
In any triangle ABC if AB > AC and D is (RBSESolutions.com) any point on BC then prove that AB > AD.
Solution.
In ∆ABC
AB > AC
⇒ ∠ACB > ∠ABC …(i) (∵ angle opposite to larger side is greater)

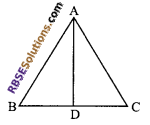
Now in ∆ACD, CD is produced to B forming an ext ∠ADB.
∠ADB > ∠ACD (exterior angle of a A is greater than each interior opposite angle)
⇒ ∠ADB > ∠ACB …(ii)
∠ACD = ∠ACB
From (i) and (ii)
∠ADB > ∠ABC
⇒ ∠ADB > ∠ABD [∵ ∠ABC = ∠ABD]
⇒ AB > AD [∵ side opposite to greater angle is larger]
Hence proved.

Question 36.
Prove that the (RBSESolutions.com) sum of three sides of a triangle is greater than the sum of its three medians.
Solution.
Given: In ∆ABC, AD, BE and CF are its medians.
To prove:
AB + BC + CA > AD + BE + CF

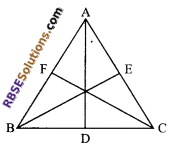
Proof: As we know that the sum of any two sides of (RBSESolutions.com) a triangle is greater than twice the median bisecting the third side. Therefore AD is the median bisecting BC
⇒ AB + AC > 2 AD
BE is the median bisecting AC
⇒ AB + BC > 2BE
Similarly for median CF
BC + AC > 2CF
Adding (i), (ii) and (iii), we get
2 (AB + BC + CA) > 2 (AD + BE + CF)
⇒ AB + BC + CA > AD + BE + CF
Hence proved.

Question 37.
In figure, O is an interior point of ∆ABC. Show that: AB + BC + CA < 2(OA + OB + OC).
Solution.
In triangle ABC, O is a point interior of ∆ABC.

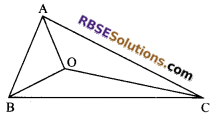
As we know that “The sum of any (RBSESolutions.com) two sides of a triangle is greater than the third side”.
OA + OB > AB …(i)
OA + OC > AC …(ii)
and OB + OC > BC …(iii)
Now, adding (i), (ii) and (iii), we get
2(OA + OB + OC) > AB + BC + CA
or AB + BC + CA < 2(OA + OB + OC)
Hence proved.

Question 38.
Prove that the sum of three altitudes of a triangle is less than the perimeter of the triangle.
Solution.
Given: A triangle ABC in which AD ⊥ BC, BE ⊥ AC and CF ⊥ AB.
To prove:
AD + BE + CF < AB + BC + CA
or AD + BE + CF < Perimeter of ∆ABC

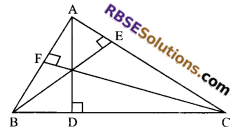
Proof: As we know that from all the segments that can (RBSESolutions.com) be drawn to a given line, from a point not lying on it, the perpendi-cular line segment is the shortest one.
AD ⊥ BC
⇒ AB > AD and AC > AD
⇒ AB + AC > 2AD …(i)
BE ⊥ AC
⇒ BC > BE and BA > BE
⇒ BC + BA > 2AB …(ii)
Also CF ⊥ AB
⇒ AC > CF and BC > CF
⇒ AC + BC > 2CF …(iii)
Adding (i), (ii) and (iii), we get
(AB + AC) + (AB + BC) + (AC + BC) > 2AD + 2BE + 2CF
⇒ 2(AB + BC + CA) > 2(AD + BE + CF)
⇒ AB + BC + CA > AD + BE + CF
⇒ Perimeter of ∆ABC > AD + BE + CF
Hence proved.

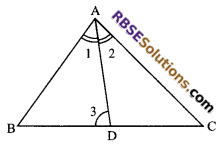
Question 39.
Prove that the’difference of any two sides of (RBSESolutions.com) a triangle is less than the third side.
Solution.
Given: A ∆ABC

To prove:
(i) AC – AB < BC
(ii) BC – AC < AB
(iii) BC – AB < AC
Construction: Take a point D on AC such that AB = AD. Join BD.
Proof: In ∆ABD AB = AD ⇒ ∠1 = ∠2 …(i)
In ∆ABD, side AD is produced to C ∠3 > ∠1 …(ii)
(ext. angle is greater than one of the opposite interior angle)
Also in ∆BCD
∠2 > ∠4 …(iii) (reason as above)
From (i) and (ii), we get
∠3 > ∠2 …(iv)
From (iii) and (iv), we get
∠3 > ∠4
⇒ BC > CD (side opposite to greater angle is larger)
⇒ CD < BC
⇒ AC – AD < BC
⇒ AC – AB < BC [∵ AD = AB]
Similarly we can prove
BC – AC < AB and BC – AB < AC
Hence proved.

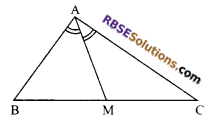
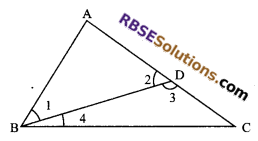
Question 40.
In figure, AD is bisector of ∠BAC then prove that AB > BD.

Solution.
In ∆ABC
AD is the bisector of ∠BAC
⇒ ∠1 = ∠2 …(i)
Also in ∆ADC
∠3 = ∠2 + ∠C (ext. angle is equal to (RBSESolutions.com) sum of opposite interior angles)
⇒ ∠3 > ∠2 (ext. angle is greater than one of the interior angles)
⇒ But ∠1 = ∠2
⇒ ∠3 > ∠1
⇒ AB > BD
Hence proved.

We hope the given RBSE Solutions for Class 9 Maths Chapter 7 Congruence and Inequalities of Triangles Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 7 Congruence and Inequalities of Triangles Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.