RBSE Solutions for Class 9 Maths Chapter 8 Construction of Triangles Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 8 Construction of Triangles Miscellaneous Exercise.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 8 |
| Chapter Name | Construction of Triangles |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 7 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 8 Construction of Triangles Miscellaneous Exercise
Question 1.
Construct a triangle whose perimeter is 12 cm and the (RBSESolutions.com) sides are in the ratio 1 : 2 : 3.
Solution.
Suppose sides of the triangle are x, 2x and 3x
Here it is given that
Perimeter of Δ = 12 cm
x + 2x + 3x = 12 cm
⇒ 6x = 12
⇒ x = 2
Sides of Δ are 2 cm, 4 cm and 6 cm.
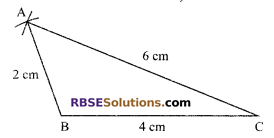
Steps of construction:
- Draw BC = 4 cm as base line.
- Take B as centre, draw an arc of radius 2 cm.
- Taking C as centre, draw an arc of radius 6 cm.
- Join A to B and C.
- Hence, ΔABC is the required triangle whose sides are in the ratio 1 : 2 : 3 and having perimeter 12 cm.
![]()
Question 2.
Construct a triangle ABC in which ∠B = 90°, ∠C = 60° and c = 5 cm.
Solution.
First, of all we will find (RBSESolutions.com) the third angle of ΔABC
i.e. ∠A = 180° – (90° + 60°) = 30°
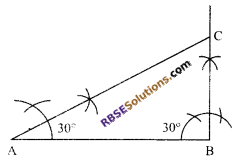
Steps of construction:
- First draw AB = 5 cm as base line.
- At B, draw an angle of 90° with the help of compass.
- Also at A, construct an angle of 30°, which meets at C.
Hence, ΔABC is the required triangle.
Question 3.
Construct a right angle triangle ABC in (RBSESolutions.com) which hypotenuse BC = 8.2 cm and one side = 4.2 cm.
Solution.
Steps of construction:
- Draw a line segment AB = 4.2 cm.
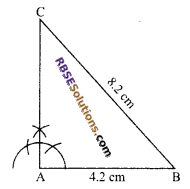
- At A, draw an angle of 90°.
- From B, draw an arc of radius 8.2 cm which cuts the line segment at C.
Hence, ΔABC is the required triangle.
Question 4.
Construct a triangle ABC in which ∠B = 45°, ∠C = 60° and the length (RBSESolutions.com) of perpendicular AD from A on BC is 4 cm.
Solution.
Steps of construction:
- Draw a straight XY as base line.
- At any point say D, on XY line segment, draw perpendicular DZ. By taking D as centre cut an arc of radius 4 cm from DZ and marked it as DA.
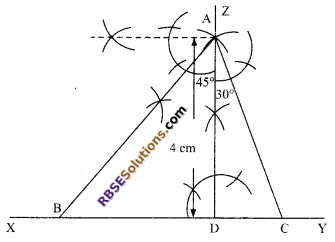
- Now, draw ∠DAB = 45° and ∠DAC = 30° which meets XY at B and C respectively.
Hence, ΔABC is the required triangle.
Question 5.
Construct (RBSESolutions.com) a triangle ABC in which a = 5.6 cm, b + c = 10.2 cm and ∠B – ∠C = 30°.
[Hint: Construct an angle of 90°+ \(\frac { 1 }{ 2 }\) (∠B – ∠C) i.e. 105° at the vertex B]
Solution.
Steps of construction:
- First of all, draw BC = 5.6 cm as base line.
- Construct an angle of 105° at B.
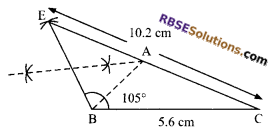
- By taking C as centre, cut an arc of radius 10.2 cm, which intersects arm of the angle ∠CBD at E. Join EC.
- Draw perpendicular bisector of EB, which intersects CE at A. Join AB. Hence, ΔABC is the required triangle.
Question 6.
Construct a triangle such that the lengths (RBSESolutions.com) of its three medians are 4.2 m, 4.8 cm and 5.4 cm respectively.
Solution.
Steps of construction:
- 1. Draw AG = 2.8 cm and produce to a point P such that AG = GP.
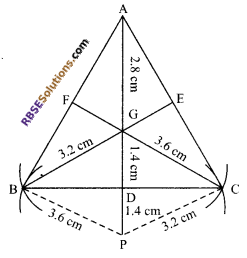
- From centre G, cut an arc
GC = \(\frac { 2 }{ 3 }\) x CF = \(\frac { 2 }{ 3 }\) x 5.4 = 3.6 cm
and from P cut an arc
CP = BG = \(\frac { 2 }{ 3 }\) x BE
= \(\frac { 2 }{ 3 }\) x 4.8 = 3.2 cm
to intersect each other at C. - From centre G, cut an arc
GB = \(\frac { 2 }{ 3 }\) x BE = 3.2 cm and from P cut an arc PB = CG = 3.6 cm to intersect each other at B. Draw BC. - Join A to B and A to C.
Hence, ΔABC is the required triangle.
![]()
Question 7.
Construct an isosceles triangle in (RBSESolutions.com) which height is 6 cm and equal sides are 7 cm. Measure the base.
Solution.
Steps of construction:
- Draw a line PQ.
- Draw perpendicular on any point on the line PQ, mark as M.
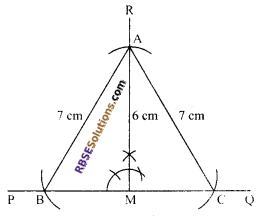
- By taking M as centre, cut an arc of radius 6 cm and mark that point as A.
- From A, cut an arc of 7 cm either side (RBSESolutions.com) of the perpendicular and mark them as B and C. Join AB and AC.
Hence, ΔABC is the required triangle.
We hope the given RBSE Solutions for Class 9 Maths Chapter 8 Construction of Triangles Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 8 Construction of Triangles Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.