RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Additional Questions.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Chapter Name | Quadrilaterals |
| Exercise | Additional Questions |
| Number of Questions Solved | 27 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Additional Questions
Multiple Choice Questions
Question 1.
In the given Q figure, ABCD is a parallelogram (RBSESolutions.com) in which ∠ADC = 130°, then ∠CBE is equal to:
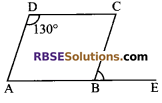
(A) 60°
(B) 130°
(C) 50°
(D) 70°
Solution
(C) 50°
Question 2.
In the given figure, PQR is a triangle in which X and Y are (RBSESolutions.com) the mid-point of the sides PR and QR respectively. If PQ = 6 cm, QR = 7 cm and PR = 8 cm, then XY is equal to:
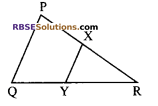
(A) 12 cm
(B) 3.5 cm
(C) 3 cm
(D) 4 cm
Solution
(C) 3 cm
![]()
Question 3.
In figure, ABCD is a parallelogram then (RBSESolutions.com) the value of x is:
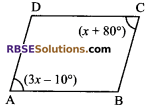
(A) 25°
(B) 60°
(C) 75°
(D) 45°
Solution
(D) 45°
Question 4.
If an angle of a parallelogram is two-third of its adjacent angle, then (RBSESolutions.com) the smallest angle of the parallelogram is:
(A) 54°
(B) 72°
(C) 84°
(D) 108°
Solution
(B) 72°
Question 5.
The ratio of the side and diagonal of a square is:
(A) 1:√2
(B) 3:√2
(C) √2:1
(D) √2:3
Solution
(A) 1:√2
Question 6.
In the given figure, ABCD is a rhombus. If ∠OAB = 35°, then (RBSESolutions.com) the value of x is:
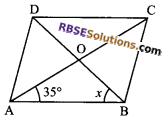
(A) 25°
(B) 35°
(C) 55°
(D) 70°
Solution
(C) 55°
Question 7.
If the two adjacent angles of (RBSESolutions.com) a parallelogram are (3x – 20°) and (50° – x), then the value of x is :
(A) 55°
(B) 75°
(C) 20°
(D) 80°
Solution
(B) 75°
Question 8.
In the given figure, ABCD is a quadrilateral and P, Q, R and S are the mid-points (RBSESolutions.com) of the sides AB, BC, CD, DA respectively. If BD =12 cm, then length of QR is:
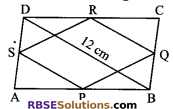
(A) 6 cm
(B) 8 cm
(C) 3 cm
(D) 4 cm
Solution
(A) 6 cm
Question 9.
In figure, D and E are mid-points (RBSESolutions.com) of the sides AB and AC respectively of ∆ABC, then measure of ∠B is:
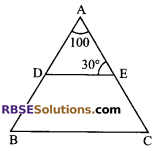
(A) 50°
(B) 30°
(C) 80°
(D) 40°
Solution
(A) 50°
Question 10.
In a quadrilateral PQRS, ∠P, ∠Q, ∠R and ∠S are interior angles. If ∠P: ∠Q: ∠R: ∠S = 1 : 2 : 3 : 4, then (RBSESolutions.com) which angle is equal to 144°.
(A) ∠P
(B) ∠Q
(C) ∠R
(D) ∠S
Solution
(D) ∠S
![]()
Very Short Answer Type Questions
Question 1.
Two consecutive angles of a parallelogram are (RBSESolutions.com) in the ratio 1 : 3. Find the smallest angle.
Solution.
Let the two consecutive angles be x and 3x.
Since the sum of two consecutive angles of a parallelogram is 180°.
Therefore, x + 3x = 180°
⇒ 4x = 180°
⇒ x = 45°
Smallest angle = 45°.
Question 2.
In the given figure, ABCD is a rectangle (RBSESolutions.com) in which ∠APB = 100°. Find the value of x.
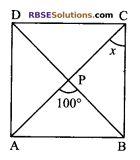
Solution.
In ΔPBC,
∠BPA + ∠BPC = 180° (linear pair of angles)
⇒ ∠BPC = 180° – 100° = 80°
⇒ ∠PCB = ∠PBC = x
⇒ x + x + 80° = 180°
⇒ 2x = 100°
⇒ x = 50°
Question 3.
The three angles of a quadrilateral measure 56°, 100° and 88°. Find the (RBSESolutions.com) measure of the fourth angle.
Solution.
Let the measure of the fourth angle be x.
As we know that sum of the angles of a quadrilateral is 360°.
56° + 100° + 88° + x = 360°
⇒ 244° + x = 360°
⇒ 360° – 244° = 116°
Hence, the measure of the fourth angle is 116°.
Question 4.
In a quadrilateral ABCD, ∠A = 3x, ∠B = 5x, ∠C = 20x and ∠D = 8x. Find the value of x.
Sol. The sum of the angles of a quadrilateral is 360°.
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ 3x + 5x + 20x + 8x = 360°
⇒ 36x = 360°
⇒ x = 10°
Question 5.
A diagonal of a rectangle is inclined to one side of the rectangle at 25°. Then find (RBSESolutions.com) the acute angle between the diagonals.
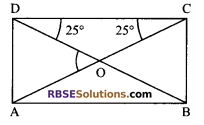
Solution.
According to figure,
In ΔOCD,
∠ODC + ∠OCD + ∠COD = 180°
⇒ 25° + 25° + ∠COD = 180°
⇒ ∠COD = 130°
Acute angle i.e. ∠DOA between the diagonals = 180° – ∠DOC = 180° – 130° = 50°
![]()
Question 6.
In the given figure, BCPQ and BCDA are two parallelograms on (RBSESolutions.com) the same base BC. Find the value of x + y.
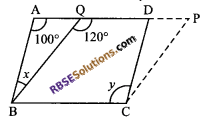
Solution.
BCDA is a parallelogram
∠A = y = 100° (opposite angles of a parallelogram are equal)
Also x + 100° = 120° (exterior angle property)
⇒ x = 20°
x + y = 20 + 100 = 120°
Question 7.
“The opposite sides of (RBSESolutions.com) a parallelogram are equal”. Prove it.
Solution.
Given: A parallelogram ABCD
To prove: AB = CD and BC = DA
Construction: Join diagonal BD.
Proof: In parallelogram ABCD, AB || DC and AD || BC
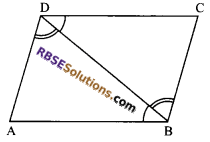
Now in Δs ABD and CBD
∠ABD = ∠CDB (alt. ∠S)
∠ADB = ∠CBD (alt. ∠S)
BD = BD
ΔABD = ΔCDB (by AAS congruencey rule)
AB = CD (by c.p.c.t)
and AD = BC
Question 8.
In figure, D and E are the mid¬points (RBSESolutions.com) of the sides AB and AC respectively of ΔABC. If BC = 6.4 cm, find DE.
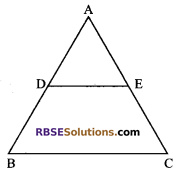
Solution.
Since, D and E are mid-points of sides AB and AC respectively. Therefore, from mid-point theorem,
DE = \(\frac { 1 }{ 2 }\) BC
⇒ DE = \(\frac { 1 }{ 2 }\) x 6.4 = 3.2
⇒ DE = 3.2 cm.
Question 9.
In the given figure, PQRS is a rectangle. If ∠RPQ = 30° then find the value of (x + y).
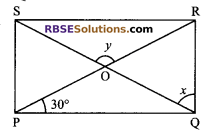
Solution.
Since, diagonal of a rectangle are equal and bisect (RBSESolutions.com) each other and vice versa.
OR = OS
⇒ ∠ORS = ∠OSR …(i)
Also PQ || SR
⇒ ∠OPQ = ∠ORS = 30° …(ii) (alt. angles)
In ΔORS,
∠ORS + ∠OSR + y = 180° (angle sum property)
⇒ 30° + 30° + y = 180° [using (i) and (ii)]
⇒ y = 120°
Also OR = OQ
⇒ ∠ORQ = ∠OQR = x
In ΔORQ,
x + x + ∠ROQ = 180°
⇒ 2x + 60° = 180° (∵ y + ∠ROQ = 180° i.e. linear pair of angles)
⇒ x = \(\frac { 120 }{ 2 }\) = 60°
x + y = 60° + 120° = 180°
Question 10.
In the given figure, AD and BE are (RBSESolutions.com) medians of ΔABC and BE || DF. Prove that CF = \(\frac { 1 }{ 4 }\) AC.
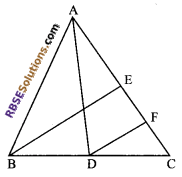
Solution.
In ΔBEC,
D is mid-point of BC and from converse (RBSESolutions.com) of mid-point theorem.
i.e. A line i.e. DF drawn through the mid-point D of BC and parallel to BE bisects the third side i.e. EC at F.
Now, F becomes the mid-point of CE.
⇒ CF = \(\frac { 1 }{ 2 }\) CE
CF = \(\frac { 1 }{ 2 }\) (\(\frac { 1 }{ 2 }\) AC)
[E is mid-point of AC ⇒ AE = EC = \(\frac { 1 }{ 2 }\) AC]
⇒ CF = \(\frac { 1 }{ 4 }\) AC
Hence proved.
![]()
Short Answer Type Questions
Question 1.
If the diagonals of a parallelogram are equal, then (RBSESolutions.com) show that it is a rectangle.
Sol.
Given: A parallelogram ABCD in which AC = BD.

To prove: Parallelogram ABCD is a rectangle
Proof: In ΔBAD and ΔABC,
AB = BA (common sides)
BD = AC (diagonals of a parallelogram are equal)
AD = BC (opposite sides of a parallelogram are equal)
ΔBAD = ΔABC (by SSS congruency rule)
⇒ ∠BAD = ∠ABC (by c.p.c.t)
But ∠BAD + ∠ABC = 180° (sum of interior angles (RBSESolutions.com) on the same side of a transversal is 180°)
⇒ 2 ∠BAD = 180° [∵ ∠BAD = ∠ABC]
⇒ ∠BAD = 90°
Hence, parallelogram ABCD is a rectangle.
Question 2.
In a trapezium ABCD, E is the mid-point of AD and EF || AB. Prove that EF = \(\frac { 1 }{ 2 }\) (AB + DC).
Solution.
Given: ABCD is a trapezium in which E is the mid-point of AD and EF || AB.
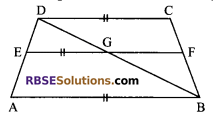
To prove: EF = \(\frac { 1 }{ 2 }\) (AB + DC)
Construction: Join BD which meets EF at G.
Proof: EF || AB (given)
EG || AB
Now in ΔADB,
E is the mid-point of AD and EG || AB.
EG bisects BD (by converse of mid-point theorem)
EG = \(\frac { 1 }{ 2 }\) AB …(i) (from mid-point theorem)
Also GF || AB and AB || DC
⇒ GF || DC
Now in ΔBCD, G is mid-point of BD and GF || DC
⇒ GF bisects BC ⇒ F is mid-point of BC
⇒ GF = \(\frac { 1 }{ 2 }\) DC …(ii)
Adding (i) and (ii), we get
EG + GF= \(\frac { 1 }{ 2 }\) AB + \(\frac { 1 }{ 2 }\) DC
⇒ EF = \(\frac { 1 }{ 2 }\) (AB + DC)
Hence proved.
Question 3.
In the given figure, PQRS is (RBSESolutions.com) a parallelogram in which PQ is produced to T such that QT = PQ. Prove that ST bisects RQ.
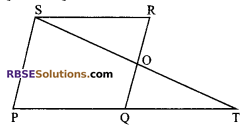
Solution.
Sol. Given: PQRS is a parallelogram in which PQ is produced to T such that PQ = QT.
To prove: QO = OR i.e. ST bisects RQ.
Proof: PQRS is a parallelogram.
PQ || RS
Now, PQ || RS and (RBSESolutions.com) transversal QR intersects them
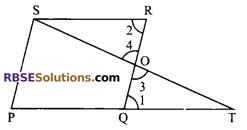
∠1 = ∠2 …(i) (alternate interior angles)
Now PQRS is a parallelogram
⇒ PQ = RS
⇒ QT = RS …(ii)
QT = PQ (given)
Thus in ΔQOT and ΔSOR, we have
∠1 = ∠2 [using (i)]
∠3 = ∠4 (vertically opposite angles)
and QT = RS [using (ii)]
ΔQOT = ΔROS (by AAS congruency rule)
⇒ QO = OR
⇒ O is the mid-point of QR
⇒ ST bisects RQ.
Long Answer Type Questions
Question 1.
Show that if the diagonals of a quadrilateral are (RBSESolutions.com) equal and bisect each other at right angles, then it is a square.
Solution.
Given: ABCD is a quadrilateral in which diagonals AC and BD are equal and bisect each other at right angles.
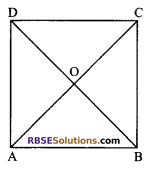
To prove: ABCD is a square.
Proof: ABCD is a quadrilateral whose diagonals bisect (RBSESolutions.com) each other. So it is a parallelogram. Also its diagonals bisect each other at right angles. So ABCD is a rhombus.
⇒ AB = BC = CD = DA
In ΔABC and ΔABD, we have
AB = AB (common sides)
BC = AD (side of a rhombus are equal)
AC = BD (given)
ΔABC = ΔBAD (by SSS congruency rule)
∠ABC = ∠BAD (by c.p.c.t)
But ∠ABC + ∠BAD = 180° (sum of the consecutive interior angles)
⇒ ∠ABC = ∠BAD = 90°
⇒ ∠A = ∠B = ∠C = ∠D = 90° (opposite angles of a parallelogram)
⇒ ABCD is a rhombus whose angles are of 90° each.
Hence, ABCD is a square.
![]()
Question 2.
In a parallelogram ABCD, E and F are the mid-points (RBSESolutions.com) of sides AB and CD respectively (see figure). Show that the line segment, AF and EC trisect the diagonal BD.
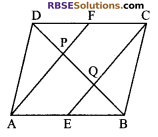
Solution.
Given: ABCD is a parallelogram in which E and F are (RBSESolutions.com) the mid-points of sides AB and CD respectively.
To prove: BQ = QP = PD
Proof: ABCD is a parallelogram
⇒ AB || DC
⇒ AE || AF and AE = CF (∵ \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) CD)
⇒ AECF is a parallelogram.
⇒ EC || AF …(i)
If ΔAPB, E is mid-point of AB (given)
and EQ ||AP [using (ii)]
⇒ Q is the mid-point PB
⇒ BQ = PQ …(ii)
Similarly, in ΔDQC, we can show that
DP = PQ
From (ii) and (iii), we have BQ = PQ = PD
Hence, line segment AF and EC trisect the diagonal BD.
Question 3.
Show that the line segment joining the mid-points (RBSESolutions.com) of the opposite sides of a quadrilateral bisect each other.
Solution.
Given: ABCD is a quadrilateral in which PR and SQ are the line segments joining the mid-points of the opposite sides.
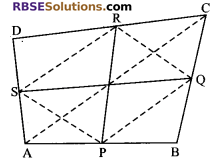
To prove: PR and SQ bisect each other.
Construction: Join PQ, QR, RS, SP and AC.
Proof: In ΔABC, P and Q are mid-points of sides AB and BC respectively.
From mid-point theorem
PQ || AC and PQ = \(\frac { 1 }{ 2 }\) AC …(i)
In ΔADC, we have
S and R are mid-points of sides AD and CD respectively.
Therefore, from mid-point theorem
SR || AC and SR = \(\frac { 1 }{ 2 }\) AC …(ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
⇒ PQRS is a parallelogram.
Reason: A quadrilateral is a parallelogram if its (RBSESolutions.com) one pair of opposite sides is equal and parallel.
Now PR and SQ are diagonals of the parallelogram PQRS.
PR and SQ bisect each other. (∵ Diagonals of a parallelogram bisect each other)
Question 4.
P, Q and R are respectively, the mid-points of sides BC, CA and AB of a triangle ABC. PR and BQ meet at X. CR and PQ meet at Y.
Prove that XY = \(\frac { 1 }{ 4 }\) BC.
Solution.
Given: ABC is a triangle in which P, Q and R are respectively the mid-points of sides BC, CA and AB. PR and BQ meet at X and CR and PQ meets at Y.
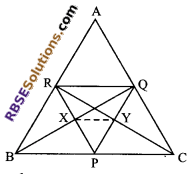
Construction:
Join X to Y.
To prove: XY = \(\frac { 1 }{ 4 }\) BC
Proof: R and Q are the mid-points of AB and AC respectively.
Therefore, RQ || BC and PQ = \(\frac { 1 }{ 2 }\) BC …(i) (by mid-point theorem)
⇒ RQ || BP and RQ = BP (∵ P is mid-point of BC)
⇒ BPQR is a parallelogram.
∵ Diagonals is (RBSESolutions.com) a parallelogram bisect each other.
∵ X is the mid-point of PR.
Similarly, PCQR is a parallelogram.
⇒ Y is the mid-point of PQ
Now in ΔPRQ, X and Y are mid-points of sides PR and PQ respectively.
⇒ XY = \(\frac { 1 }{ 2 }\) RQ …… (ii)
From (i) and (ii), we get
XY = \(\frac { 1 }{ 2 }\) RQ
= \(\frac { 1 }{ 2 }\) (\(\frac { 1 }{ 2 }\) BC)
= \(\frac { 1 }{ 4 }\) BC
Hence, XY = \(\frac { 1 }{ 4 }\) BC.
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 9 Quadrilaterals Additional Questions, drop a comment below and we will get back to you at the earliest.