RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Ex 9.2.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Chapter Name | Quadrilaterals |
| Exercise | Ex 9.2 |
| Number of Questions Solved | 17 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Ex 9.2
Question 1.
In figure, ABCD and AEFG are (RBSESolutions.com) both parallelograms. If ∠C = 55° then find the value of ∠F.
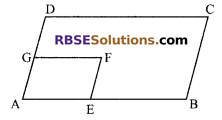
Solution.
∵ ABCD is a parallelogram.
⇒ ∠A = ∠C = 55°
(in a parallelogram, opposite angles are equal)
Also AEFG is a parallelogram.
∴ ∠A = ∠F = 55°.
Question 2.
Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
Solution.
No, angle sum property of a quadrilateral is always equal to 360°. If all the angles would be acute then sum of all the angles could not reach to 360°.
![]()
Question 3.
Can all the angles of a quadrilateral be (RBSESolutions.com) right angles? Give reason for your answer.
Solution.
Yes, angle sum of a quadrilateral is 360°. In this situation quadrilateral will become either a square or a rectangle.
Question 4.
Diagonals of a quadrilateral bisect each other. If ∠A = 35° then find ∠B.
Solution.
∵Diagonals of a quadrilateral bisect each other. It means it is a parallelogram.
∴ ∠A + ∠B = 180°
(sum of interior angles on the same side of a transversal is 180°)
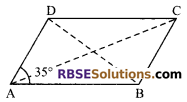
⇒ 35° + ∠B = 180°
⇒ ∠B = 145°.
Question 5.
Opposite angles of a quadrilateral (RBSESolutions.com) are equal.If AB = 4 cm then determine the length of CD.
Solution.
∵Opposite angles of a quadrilateral are equal. It means it is parallelogram and in parallelogram opposite sides are equal.
∴ CD = AB = 4 cm.
Question 6.
ABCD is a rhombus in which altitude drawn from D to AB bisects AB. Find the angles of a rhombus.
Solution.
Let side of rhombus be x

∴ ∆ABD is an equilateral triangle.
⇒ ∠A = 60°
⇒ ∠A + ∠D = 180°
⇒ ∠D = 120°
⇒ ∠A = 60°, ∠B = 120°,
∠C = 60°, ∠D = 120°.
Question 7.
Through A, B and C, lines RQ, PR and QP have been (RBSESolutions.com) drawn respectively parallel to sides BC, CA and AB of a ∆ABC as shown in figure. Show that BC = \(\frac { 1 }{ 2 }\)QR.
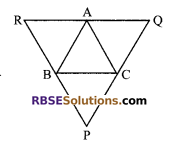
Solution.
Given: PQ || AB, PR || AC and RQ || BC.
To show that
BC = \(\frac { 1 }{ 2 }\)QR
Proof: In quadrilateral BCAR,
∵ BR || CA and BC || RA
⇒ BCAR is a parallelogram.
⇒ BC = AR …(i)
Now, in quadrilateral BCQA,
BC || AQ and AB || QC
⇒ BCQA is (RBSESolutions.com) a parallelogram.
⇒ BC = AQ …(ii)
On adding (i) and (ii), we get
2BC = AR + AQ
⇒ 2BC = RQ
⇒ BC = \(\frac { 1 }{ 2 }\)QR
Hence proved.
![]()
Question 8.
D, E and F are the mid-points of the sides BC, CA and AB respectively of a ∆ABC. Show that ∆DEF is (RBSESolutions.com) also an equilateral triangle.
Solution.
∵ D, E and F are mid-points of sides BC,CA and AB respectively
∴ Using mid point theorem
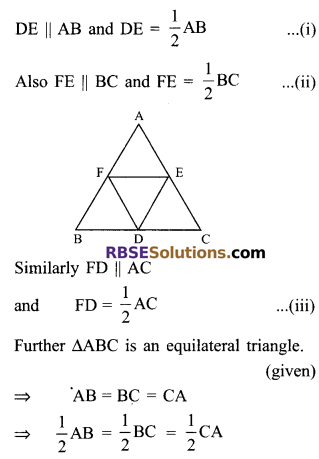
By using (i), (ii) and (iii), we get
DE = FE = FD
⇒ ∆DEF is an equilateral triangle.
Question 9.
The points P and Q have been taken on opposite sides AB and CD respectively of (RBSESolutions.com) a parallelogram ABCD in such a way that AP = CQ (see figure).
Show that AC and PQ bisect each other.
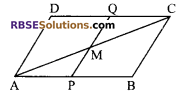
Solution.
Given: ABCD is a parallelogram such that AP = CQ.
To prove: AC and PQ bisect each other.
∠MAP = ∠MCP
(alternate angles)
AP = CQ (given)
∠APM = ∠CQM
(alternate angles)
∴ ∆AMP ≅ ∆CMQ
(by ASA congruency rule)
⇒ AM = CM
and PM = QM (by c.p.c.t)
⇒ AC and PQ bisect each other.
Question 10.
E is the mid-point of the side AD of (RBSESolutions.com) a trapezium ABCD in which AB || DC. Through E parallel to AB a line intersects BC at F. Show that F will be the mid-point of sides BC.
Solution.
Given: ABCD is a trapezium in which AB || DC and E is mid-point of AD.
Construction: Draw EF || AB and join A to C.
To prove: F is mid-point of BC.
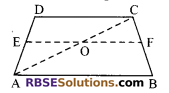
Proof: In ∆ADC, E is mid-point of AD and EO is drawn parallel to AB i.e., parallel to DC also. Then (RBSESolutions.com) by using converse of mid- point theorem, O will be the mid-point of AC.
Similarly, in ∆ABC, O is the mid-point of AC and OF || AB.
⇒ F will be the mid-point of BC.
(by converse of mid-point theorem)
Question 11.
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are the mid-points of sides AB and BC respectively, then find the length of side DE.
Solution.
In ∆ABC, D and E are mid-points (RBSESolutions.com) of sides AB and BC respectively.
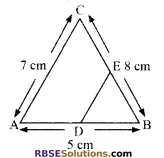
∴ Using mid-point theorem,
DE = \(\frac { 1 }{ 2 }AC\) = \(\frac { 1 }{ 2 }X7cm\) = 3.5 cm
![]()
Question 12.
In figure, it is given that BDEF and FDCE are (RBSESolutions.com) parallelograms. Can you say that BD = CD? Why or why not?
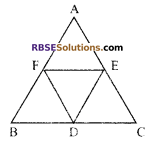
Solution.
∵ It is given that BDEF and FDCE are parallelograms.
⇒ BD = FE ….(i)
(opposite side of parallelogram are equal)
Also DC = FE …(ii)
(reason as above)
⇒ BD = CD [from (i) and (ii)]
Question 13.
In figure, D, E and F are the mid-points (RBSESolutions.com) of the sides BC, CA and AB respectively. If AB = 4.3 cm, BC = 5.6 cm and AC = 3.9 cm, then find the perimeter of the following:
(i) ADEF and
(ii) quad. BDEF
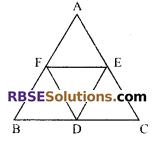
Solution.
(i) Using mid-point theorem i.e., the line joining the mid-point of two sides of (RBSESolutions.com) a triangle is parallel to third side and half of it.

∴ Perimeter of ∆DEF
= DE + FE + DF
= 2.15 + 2.8 + 1.95 = 6.9 cm
(ii) Perimeter of quad. BDEF
= BD + DE + EF + FB
= 2.8 + 2.15 + 2.8 + 2.15
= 9.9 cm.
Question 14.
Show that the line segment joining the mid-points (RBSESolutions.com) of the consecutive sides of a square is also a square.
Solution.
Given: ABCD is a square in which E, F, G and H are respectively the mid-points of sides AB, BC, CD and DA.
To prove: EFGH is a square.
Construction: Join A to C and similarly B to D.
Proof: In ∆ABC
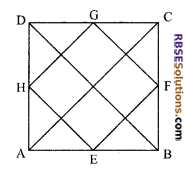
∵ E and F are mid points of sides AB and BC
∴ From mid-point theorem
EF = \(\frac { 1 }{ 2 }\)AC …(i)
Similarly, HG = \(\frac { 1 }{ 2 }\) AC …(ii)
From (i) and (ii) EF = HG
Similarly, by joining B to D.
We can say HE = GF
Again by using (RBSESolutions.com) mid-point theorem,
Since ABCD is a square
∴ AB = BC = CD = DA
⇒ \(\frac { 1 }{ 2 }\)AB = \(\frac { 1 }{ 2 }\)DA
⇒ AE = AH
⇒ ∠AHE = ∠AEH = 45°
Similarly, ∠DHG = ∠DGH = 45°
∴∠AHE + ∠GHE + ∠DHG = 180°
(straight angle)
⇒ 45° + ∠GHE + 45° = 180°
∠GHE = 90°
⇒ EFGH is a square.
![]()
Question 15.
The diagonals of a quadrilateral are perpendicular to each other. Show (RBSESolutions.com) that the quadrilateral, formed by joining the mid-points of its sides is a rectangle.
Solution.
Given: A quadrilateral whose diagonals AC = BD are perpendicular to each other P, Q, R, S are the mid-points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.
To prove: PQRS is a rectangle.
Proof: In ∆ABC, P and Q are the mid-points of AB and BC respectively.
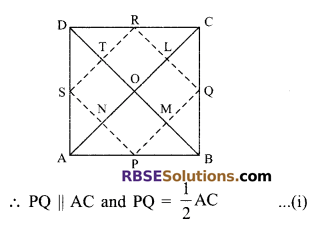
(Using the mid-point theorem)
In ∆ADC, R and S are the (RBSESolutions.com) mid-points of CD and AD respectively.
RS || AC and RS = \(\frac { 1 }{ 2 }\)AC …(ii)
(same reason as above)
From (i) and (ii)
PQ || RS and PQ = RS
(pair of opposite sides are equal and parallel)
So, PQRS is a parallelogram.
Suppose diagonals AC and BD of quadrilateral ABCD intersect at O. Now in ∆ABD, P is the mid-point of AB and S is the mid-point of AD.
∴ PS || BD => PN || OM
Also from (i) PQ || AC => PM || ON
Hence, quadrilateral PMON is (RBSESolutions.com) a parallelogram.
⇒ ∠MPN = ∠MON
(opposite angles of a parallelogram are equal)
⇒ ∠MPN = ∠BOA (∵ ∠BOA = ∠MON)
⇒ ∠MPN = 90°
⇒ ∠QPS = 90°
Thus, PQRS is a parallelogram whose one angle ∠QPS = 90°.
Hence, PQRS is a rectangle.
Question 16.
Prove that in a right-angled triangle, the median bisecting (RBSESolutions.com) the hypotenuse is half of the hypotenuse.
Solution.
Given: ∆ABC is a right angled triangle, right angled at B and BD is its median.
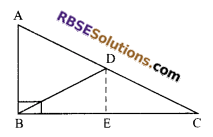
To prove: BD = \(\frac { 1 }{ 2 }\)AC
Construction: Draw DE perpendicular on BC.
Proof: DE ⊥ BC (by construction)
and D is the mid-point of hypotenuse AC.
∴BE = EC
(by converse of mid-point theorem)
Now, ∆’s DBE and DEC
BE = EC
DE = DE (common side)
∠DEB = ∠DEC = 90°
(by construction)
∴∆DBE ≅ ∆DEC
(by SAS congruency)
⇒ DC = DB …(i)
Again, D is mid-point of AC
2DC = AC …(ii)
From (i) and (ii), we get
⇒ 2DB = AC
⇒ BD = \(\frac { 1 }{ 2 }\)AC Hence proved.
Question 17.
Prove that the quadrilateral formed by joining (RBSESolutions.com) the mid-points of the consecutive sides of a rectangle is a rhombus.
Solution.
Given: A rectangle ABCD in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively.
Join PQ, QR, RS and SP respectively.
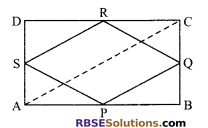
To prove: PQRS is a rhombus.
Construction: Join AC
Proof: In ∆ABC, P and Q are the mid-point of sides AB and BC respectively.
Therefore, PQ || AC and PQ = \(\frac { 1 }{ 2 }\)AC …(i)
(by mid-point theorem)
Also in ∆ADC
SR || AC and SR = \(\frac { 1 }{ 2 }\)AC …(ii)
From (i) and (ii), we get
PQ || SR and PQ = SR …(iii)
⇒ PQRS is (RBSESolutions.com) a parallelogram.
Now ABCD is a rectangle. (given)
⇒ AD = BC
⇒ \(\frac { 1 }{ 2 }\)AD = \(\frac { 1 }{ 2 }\)BC => AS = BQ ,..(iv)
⇒ In ∆’s APS and BPQ, we have
AP = BP
(∵ P is the mid-point of AB)
∠PAS = ∠PBQ = 90°
and AS = BQ from (iv)
So, ∆APS ≅ ∆BPQ
(by SAS congruency property)
⇒ PS = PQ …(v)
From (iii) and (v), we obtain that PQRS is a parallelogram such that
PS = PQ
Hence, PQRS is a rhombus.
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2, drop a comment below and we will get back to you at the earliest.